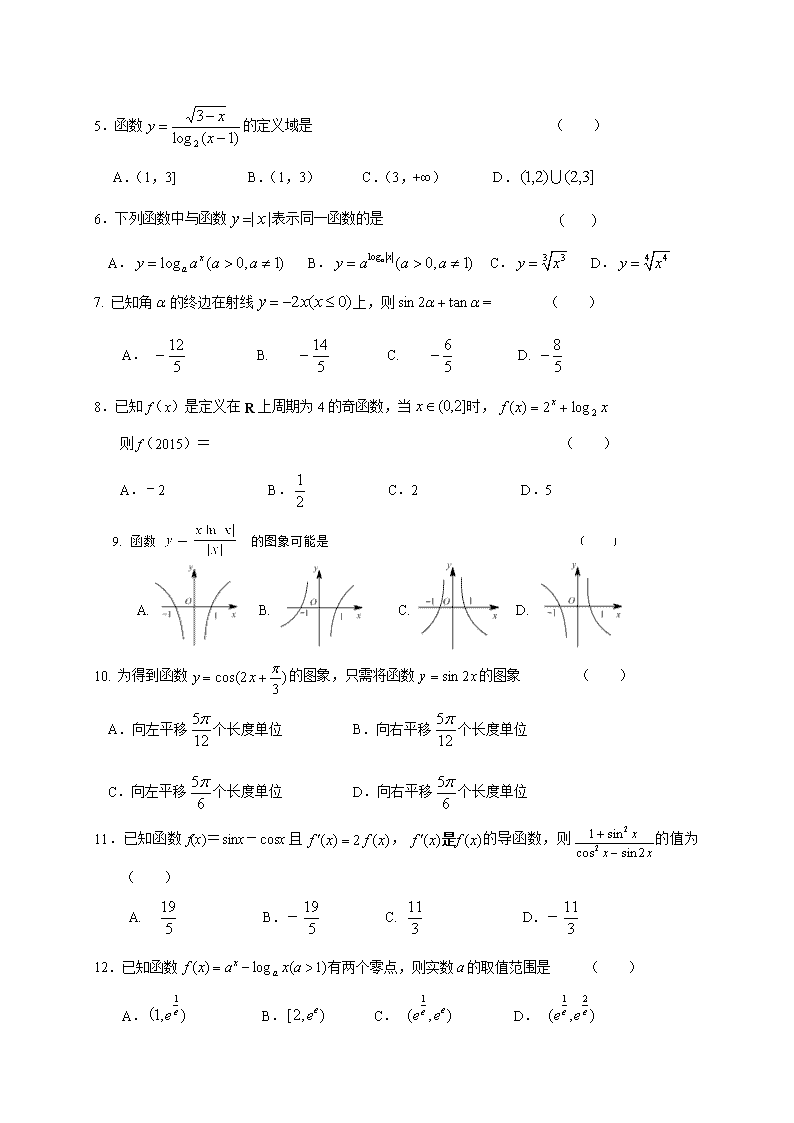- 359.00 KB
- 2021-04-21 发布
大庆四中2018~2019学年度第二学期第三次检测高二年级
数学(文科)试题
考试时间:120分钟 分值:150分
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分
第Ⅰ卷(选择题共60分)
注意事项:
1、答第I卷前,考生务必将自己的姓名、准考证号填写在答题卡上;条形码粘贴在指定位置.
2、每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.在试卷纸上作答无效.如需作图先用铅笔定型,再用黑色签字笔描绘。
一、选择题:(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知集合N),则集合等于( )
A.{-1,1} B.{-1,0,1} C.{0,1} D.{1}
2.在复平面内,复数(为虚数单位)对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.命题“a,b都是偶数,则a与b的和是偶数”的逆否命题是 ( )
A.a与b的和是偶数,则a,b都是偶数
B.a与b的和不是偶数,则a,b都不是偶数
C.a,b不都是偶数,则a与b的和不是偶数
D.a与b的和不是偶数,则a,b不都是偶数
4.下列命题正确的是 ( )
A. 的图像是一条直线
B. 幂函数的图像都经过点
C. 若幂函数是奇函数,则在区间(0,+)上是增函数
D. 幂函数 在区间(0,+)上,随着的增大而增大
5.函数的定义域是 ( )
A.(1,3] B.(1,3) C.(3,+∞) D.
6.下列函数中与函数表示同一函数的是 ( )
A. B. C. D.
7. 已知角的终边在射线上,则= ( )
A. B. C. D.
8.已知f(x)是定义在R上周期为4的奇函数,当时,
则f(2015)= ( )
A.﹣2 B. C.2 D.5
9. 函数 的图象可能是
A. B. C. D.
10. 为得到函数的图象,只需将函数的图象 ( )
A.向左平移个长度单位 B.向右平移个长度单位
C.向左平移个长度单位 D.向右平移个长度单位
11.已知函数f(x)=sinx-cosx且,的导函数,则的值为 ( )
A. B.- C. D.-
12.已知函数有两个零点,则实数的取值范围是 ( )
A. B. C. D.
二、填空题:(本大题共4小题,每小题5分,满分20分.)
13. 将2400o化为弧度制______________
14.
15.
16.若函数满足, 则当x>0时,的取值范围是
三、解答题:(本大题共6小题,满分70分. 解答须写出文字说明,证明过程和演算步骤.)
17.(本小题满分10分)
已知在直角坐标系xOy中,曲线C的参数方程为,
直线l经过定点,倾斜角为.
(Ⅰ)写出直线l的参数方程和圆的标准方程;
(Ⅱ)设直线l与圆相交于A,B两点,求|PA|•|PB|的值.
18.(本小题满分12分)
已知函数.
(Ⅰ)求的定义域与最小正周期;
(Ⅱ)当时,求值域.
19.(本小题满分12分)
设函数f(x)=x3﹣3ax2+3bx的图象与直线12x+y﹣1=0相切与点(1,﹣11).
(Ⅰ)求a,b的值;
(Ⅱ)讨论函数f(x)的单调性,并求函数的极值;
(III) 若函数在(m,m2+2m)上为减函数,求m的取值范围.
20.(本小题满分12分)
在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,半圆C的极坐标方程为ρ=2cosθ,θ∈.
(Ⅰ)求C的参数方程;
(Ⅱ)设点D在C上,C在D处的切线与直线l:y=x+2垂直,根据(1)中你得到的参数方程,确定D的坐标.
21.(本小题满分12分)
设函数.
(Ⅰ)求函数的单调增区间;
(Ⅱ)当x∈[0,π)时,求使的所有x的和.
22. (本小题满分12分)
设函数,R.
(Ⅰ)讨论函数的单调性;
(Ⅱ)当时,求证:函数的最小值小于1.
大庆四中2018~2019学年度第二学期第三次检测高二年级
数学(文科)试题答案
AADD.D. DB.ABA. BA.
二、填空题:
13. 14. 15. 16.(1,2]
三、解答题:
17. 解:(1)直线l经过定点P(1),倾斜角为,
可得直线的参数方程为(t为参数),即(t为参数);
曲线C的参数方程为(θ为参数),可得圆的标准方程为x2+y2=4;
(2)将直线的参数方程代入圆的标准方程,
可得(1+t)2+(+t)2=4,化为t2+(1+)t﹣1=0,
设t1,t2是方程的两个实根,则t1t2=﹣1,则|PA|•|PB|=|t1|•|t2|=|t1t2|=1.
18.(本小题满分12分)
解:(Ⅰ)对于函数,
由,可得f(x)的定义域为.
所以f(x)的最小正周期.
(Ⅱ)由,得,
,,
∴,∵,,∴.
19.(本小题满分12分)
解:(1)求导得f′(x)=3x2﹣6ax+3b.由于与直线12x+y﹣1=0相切于点(1,﹣11),
所以f(1)=﹣11,f′(1)=﹣12,即:
1﹣3a+3b=﹣11①,
3﹣6a+3b=﹣12②, 由①②解得:a=1,b=﹣3;
(2)由a=1,b=﹣3得:f(x)=x3﹣3x2﹣9x,
f′(x)=3x2﹣6ax+3b=3(x2﹣2x﹣3)=3(x+1)(x﹣3)
令f′(x)>0,解得x<﹣1或x>3;
又令f′(x)<0,解得﹣1<x<3.
故当x∈(﹣∞,﹣1)时,f(x)是增函数,当x∈(3,+∞)时,f(x)也是增函数,
当x∈(﹣1,3)时,f(x)是减函数.
∴f(x)极大值=f(﹣1)=5,f(x)极小值=f(3)=﹣27.
(3)由题意得:,解得0<m≤1.
20.(本小题满分12分)
解:(1)C的普通方程为
(x-1)2+y2=1(0≤y≤1). 可得C的参数方程为 (t为参数,0≤t≤π).
(2)设D(1+cost,sint).由(1)知C是以G(1,0)为圆心,1为半径的上半圆.因为C在点D处的切线与l垂直,所以直线GD与l的斜率相同,tant=,t=.
故D的直角坐标为,即.
21.(本小题满分12分)
解:(1)函数=sinxcosx+cos2x﹣cos2x+=sin2x﹣•+=sin(2x﹣),
故它的周期为T=π.
当x∈[0,π)时,,所以当
,所以满足条件的x的和为
22.(本小题满分12分)
解:(1)f(x)的定义域为(0,+∞),==
,
当a≤0时,f'(x)>0,f(x)在(0,+∞)上单调递增;
当a>0时,当x∈(0,a),f'(x)<0,f(x)单调递减;
当x∈(a,+∞),f'(x)>0,f(x)单调递增;
综上,当a≤0时,f(x)在(0,+∞)上单调递增;
当a>0时,f(x)在(0,a)上单调递减,在(a,+∞)上单调递增.
(2)证明:由(1)知,f(x)min=f(a)==,
即.
解法一:=,,
∴g'(a)单调递减,
又g'(1)>0,g'(2)<0,所以存在a0∈(1,2),使得g'(a0)=0,
∴当a∈(0,a0)时,g'(a)>0,g(a)单调递增;
当a∈(a0,+∞)时,g'(a)<0,g(a)单调递减;
∴g(a)max=g(a0)=,又g'(a0)=0,即,,
∴=,令t(a0)=g(a0),则t(a0)在(1,2)上单调递增,
又a0∈(1,2),所以t(a0)<t(2)=2﹣1=1,∴g(a)<1.
解法二:要证g(a)<1,即证,即证:,
令,则只需证,=,
当a∈(0,2)时,h'(a)<0,h(a)单调递减;
当a∈(2,+∞)时,h'(a)>0,h(a)单调递增;
所以h(a)min=h(2)=,
所以h(a)>0,即g(a)<1.