- 1.74 MB
- 2021-04-21 发布
福建省福州市2020届高三上学期期末质量检测数学试题(文)
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设复数,则( )
A. B.
C. 3 D. 5
【答案】B
【解析】,故.
故选:B.
2.已知集合或,,则( )
A. B.
C. D.
【答案】D
【解析】集合并无包含关系,故A,B均错误.又,或故C错误. 正确.
故选:D.
3.执行如图所示的程序框图,若输入的分别为4,2,则输出的( )
A. 2 B. 3
C. 4 D. 5
【答案】C
【解析】根据流程,输入4,2,.
,不满足.
,不满足.
,满足.输出.
故选:C.
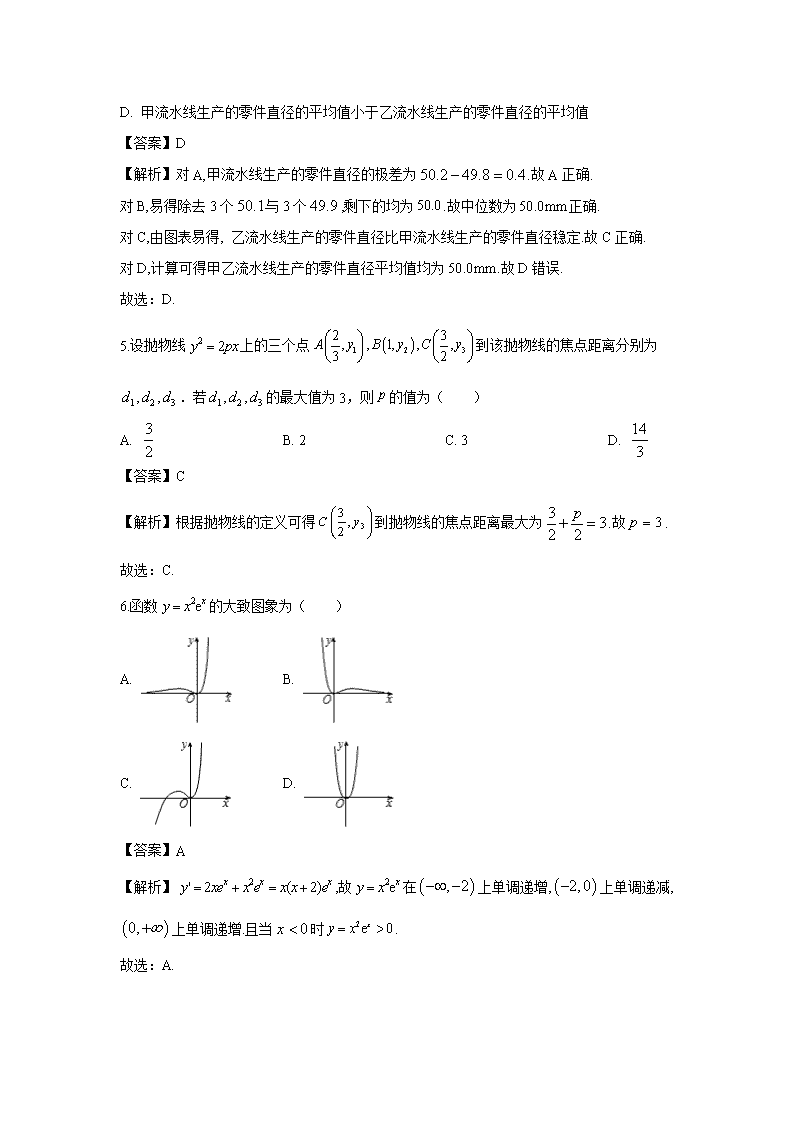
4.某工厂有甲、乙两条流水线同时生产直径为的零件,各抽取10件进行测量,其结果如下图所示,则以下结论不正确的是( )
A. 甲流水线生产的零件直径的极差为
B. 乙流水线生产的零件直径的中位数为
C. 乙流水线生产的零件直径比甲流水线生产的零件直径稳定
D. 甲流水线生产的零件直径的平均值小于乙流水线生产的零件直径的平均值
【答案】D
【解析】对A,甲流水线生产的零件直径的极差为.故A正确.
对B,易得除去3个与3个,剩下的均为.故中位数为正确.
对C,由图表易得, 乙流水线生产的零件直径比甲流水线生产的零件直径稳定.故C正确.
对D,计算可得甲乙流水线生产的零件直径平均值均为.故D错误.
故选:D.
5.设抛物线上的三个点到该抛物线的焦点距离分别为.若的最大值为3,则的值为( )
A. B. 2 C. 3 D.
【答案】C
【解析】根据抛物线的定义可得到抛物线的焦点距离最大为.故.
故选:C.
6.函数的大致图象为( )
A. B.
C. D.
【答案】A
【解析】,故在上单调递增,上单调递减,上单调递增.且当时.
故选:A.
7.设满足约束条件则的最大值为( )
A. 1 B. 3
C. 4 D. 5
【答案】D
【解析】画出可行域,又,
易得在处取得最大值.
故选:D.
8.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(米堆所成的几何体的三视图如图所示).米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.6立方尺,圆周率,估算出堆放的米约有( )
A. 20斛 B. 21斛 C. 22斛 D. 23斛
【答案】C
【解析】由题得该米堆为四分之一的圆锥.故体积立方尺.
即斛.
故选:C.
9.已知函数的部分图象如图所示,则的单调递减区间为( )
A.
B.
C.
D.
【答案】A
【解析】易得周期满足,故.且图中最高点横坐标.故一个单调区间为.
又函数周期为.故单调递减区间为.
故选:A.
10.若,则( )
A. B.
C. 或 D. 或或3
【答案】C
【解析】由可得
.故或.
即或.
故选:C.
11.已知函数,直线与曲线相切,则( )
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】设切点为,则,又直线与曲线相切故,消去有,代入第一个式子有
.易得.代入有.
故选:B.
12.已知双曲线()的左、右焦点分别为,若上点满足,且的取值范围为,则的离心率的取值范围是( )
A. B. C. D.
【答案】B
【解析】由双曲线的定义有,又,故,.
故.又的取值范围为,
故.即.
故.
故选:B.
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分.
13.已知向量满足,与的夹角为,则______.
【答案】
【解析】易得.
故答案为:
14.已知函数若,则______.
【答案】
【解析】由题,且,故.当时无解.
当时,成立.
故答案为:
15.在钝角中,已知,若的面积为,则的长为______.
【答案】
【解析】由题意得, .
又钝角,当为锐角时,,则
,即不满足钝角三角形.
故为钝角.此时.故.
即
故答案为:.
16.已知正方体的棱长为2,直线平面.平面截此正方体所得截面有如下四个结论:
①截面形状可能为正三角形;
②截面形状可能为正方形;
③截面形状不可能是正五边形;
④截面面积最大值为.
其中所有正确结论的编号是______.
【答案】①③④
【解析】对①,当截此正方体所得截面为时满足.故①正确.
对②,由对称性得,截面形状不可能为正方形.故②错误.
对③,由对称性得截面形状不可能是正五边形,故③正确.
对④,当截面为正六边形时面积最大,为.故④正确.
故答案为:①③④
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.垃圾分一分,城市美十分;垃圾分类,人人有责.某市为进一步推进生活垃圾分类工作,调动全民参与的积极性,举办了“垃圾分类游戏挑战赛”.据统计,在为期个月的活动中,共有万人次参与.为鼓励市民积极参与活动,市文明办随机抽取名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
单次游戏得分
频数
(1)根据数据,估计参与活动的网友单次游戏得分的平均值及标准差(同一组中的数据用该组区间的中点值作代表);(其中标准差的计算结果要求精确到)
(2)若要从单次游戏得分在、、的三组参与者中,用分层抽样的方法选取人进行电话回访,再从这人中任选人赠送话费,求此人单次游戏得分不在同一组内的概率.
附:,.
解:(1)参与该活动的网友单次游戏得分的平均值
.
标准差
(2)用分层抽样抽取人,其中得分在的有人,得分在的有人,得分在的有人,
分别记为,,,人中任选人,
有、、、、、、、、、、、、、、、、、、、、,共 种结果,
其中人得分在同一组的有种,分别是、、、、、、,
故人得分不在同一组内的概率.
18.已知数列的前项和,且成等比数列.
(1)求数列的通项公式;
(2)设,求数列的前项和.
解:(1)当时,
当时,,
经检验,时也满足上式,所以.
因为成等比数列,
所以,
即,解得.
所以
(2)由(1)及题设得,,
所以
.
19.如图,在四棱锥中,底面为正方形,底面,,为线段的中点,为线段上的动点.
(1)平面与平面是否互相垂直?如果垂直,请证明;如果不垂直,请说明理由.
(2)若,为线段的三等分点,求多面体的体积.
解:(1)解法一:(1)平面与平面互相垂直,
理由如下:
因为底面,平面,
所以.
因为为正方形,所以
又,且平面,
所以平面.
因为平面,所以
因为,为线段的中点,所以,
又,且平面,
所以平面,
因为平面,所以平面平面.
(2)因为底面,为线段的中点,
所以点到底面的距离为,
则,
又为线段的三等分点,
当时,,
所以多面体的体积为;
当时,,
所以多面体的体积为.
综上,多面体的体积为或.
解法二:(1)平面与平面互相垂直,
理由如下:
因为底面,平面,所以平面底面,
又平面底面,,平面,
所以平面.
因为平面,所以
因为,为线段的中点,所以,
又,且平面,
所以平面,
因为平面,
所以平面平面
(2)同解法一.
20.已知圆,椭圆()短轴长等于圆半径的
倍,的离心率为.
(1)求的方程;
(2)若直线与交于两点,且与圆相切,证明:.
解:解法一:(1)依题意,圆半径等于,
因为椭圆的短轴长等于圆半径的倍,
所以,解得
因为的离心率为,所以, ①
又因为,所以, ②
联立①② ,解得,
所以的方程为.
(2)证明:①当直线斜率不存在时, 直线的方程为,或.
当时,,则,故.
同理可证,当时,.
②当直线斜率存在时,设其方程为
因为直线与圆相切,所以,即,
由得,,
所以,且
所以
,
所以
综上,
解法二:(1)同解法一
(2)①当直线方程为时, ,则
,故
同理可证,当直线方程为时,
②当直线不与轴平行时,设其方程为
因为直线与圆相切,所以,即
由得,
所以,且
,
所以,.
综上,
21.已知函数在上的最大值为.
(1)求的值;
(2)证明:函数在区间上有且仅有2个零点.
(1)解:,
因为,所以,又,
所以,即.
当时,,所以在区间上递增,
所以,解得.
当时,,所以在区间上递减,
所以,不合题意.
当,,不合题意.
综上,.
(2)证明:设,
则,
所以在上单调递减,又,
所以存在唯一的,使得
当时,,即,所以上单调递增;当
时,,即,所以上单调递减
又,
所以在与上各有一个零点,
综上,函数在区间上有且仅有两个零点.
(二)选考题:共10分.请考生在第22,23两题中任选一题作答.如果多做,则按所做第一个题目计分,作答时请用2B铅笔在答题卡上将所选题号后的方框涂黑.
22.在直角坐标系中,直线的参数方程为(为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求C的直角坐标方程;
(2)设点M的直角坐标为, l与曲线C的交点为,求的值.
解:(1)由,得.
将代入得,,
所以C的直角坐标方程为.
(2)设所对应的参数分别为,
因为直线l的参数方程为为参数
所以M在l上
把l的参数方程代入可得
所以,
所以,
故=.
23.已知函数的最小值为.
(1)求的值;
(2)若为正实数,且,证明:.
解:(1)根据题意,函数
所以为在单调递减,在单调递增,
所以
(2)由(1)知,,所以
又因为为正实数,
,,,
所以,即,
所以,
即.