- 1.47 MB
- 2021-04-20 发布
天一大联考
2016——2017学年毕业班阶段性测试(三)
数学(文科)
第Ⅰ卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.
1.已知集合,则
A. B. C. D.
2.定义.已知复数,则在复平面内,复数所对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3. 在长方形ABCD中,E,F分别是AB边上靠近A,B的四等分点,G是CD的中点,若,,则
A. B. C. D.
4.已知,若,则
A. 0 B. 1 C. 9 D. -9
5.已知正六边形中,P,Q,R分别是边AB,EF,CD的中点,则向正六边形ABCDEF内投掷一点,该点落在内的概率为
A. B. C. D.
6.已知,,则
A. B. C. D.
7.割圆术是公元三世纪我国古代数学家刘徽创造的一种求圆的周长和面积的方法:随着圆内正多边形边数的增加,它的周长和面积越来越接近圆的周长和面积.“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽就是大胆地应用了直代曲,无限趋近的思想方法求出了圆周率.某同学利用刘徽的“割圆术”思想设计的一个计算圆周率的近似值的程序图如图所示,则输出的S的值为(参考数据:)
A. B. 3 C. D.
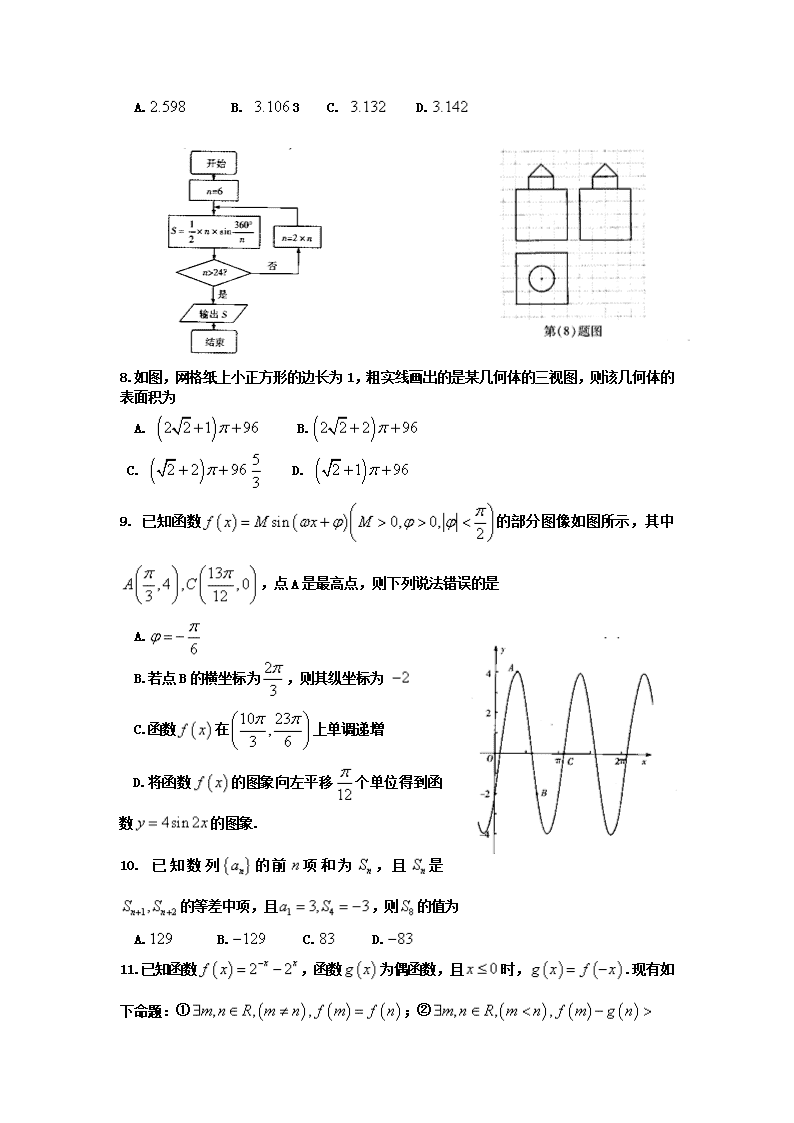
8.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为
A. B.
C. D.
9. 已知函数的部分图像如图所示,其中,点A是最高点,则下列说法错误的是
A.
B.若点B的横坐标为,则其纵坐标为
C.函数在上单调递增
D.将函数的图象向左平移个单位得到函数的图象.
10. 已知数列的前项和为,且是的等差中项,且,则的值为
A. B. C. D.
11.已知函数,函数为偶函数,且时,.现有如下命题:①;②
.则上述两个命题:
A. ①真②假 B. ①假②真 C. ①②都假 D. ①②都真
12.已知函数,若对任意的,总存在,使得,则实数的取值范围为
A. B.
C. D.
二、填空题:本大题共4小题,每小题5分,共20分.
13. 已知实数满足,则的取值范围为 .
14.已知抛物线上的第四象限的点到焦点F的距离为,则点M到直线的距离为 .
15. 已知圆C(圆心C在第一象限内)过点(1,0),(7,0),直线截圆C的弦长为,则圆C的标准方程为 .
16. 如图,在四面体中,点O是点P在平面ABC上的投影,且,则四面体的外接球的体积为 .
三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程.
17.(本题满分10分)
已知等差数列的公差为,若,且成等比数列.
(1)求数列的通项公式;
(2)若,数列的通项公式为,求数列的前项和.
18.(本题满分12分)
如图所示,在中,B,C分别为AD,AE上的点,若,
(1)求的值;
(2)记的面积为,四边形BCED的面积为,若,求的最大值.
19.(本题满分12分)
为了了解“喝茶”对“患癌症”是否有影响,现对300名不同地区的居民进行身体状况的调查,得到如图所示的列联表:
28. 完成上述列联表,并判断是否有99.9%的把握认为“喝茶”对“患癌症”有影响;
29. 在上述患癌症的人群中按照喝茶情况进行分层抽样,抽取8名进行基本情况登记,再从中随机选取2人进行调查,求至少有1人每日喝茶超过60ml的概率.
20. (本题满分12分)已知三棱柱中,底面三角形ABC时直角三角形,四边形和四边形均为正方形,分别是的中点,
(1)证明:平面;
(2)求三棱锥的体积.
21.(本题满分12分)如图,O为坐标原点,椭圆的离心率为,以椭圆C的长轴长、短轴长分别为邻边的矩形的面积为8.
(1)求椭圆C的标准方程;
(2)若是椭圆上的两个动点,且,试问:是否是定值?若是,求出定值,若不是,请说明理由.
22.(本题满分12分)
已知函数
(1)求曲线在处的切线方程;
(2)若关于的方程在上有两个不同的实数根,求
的取值范围.