- 313.89 KB
- 2021-04-20 发布
考点规范练9 函数的图象
基础巩固组
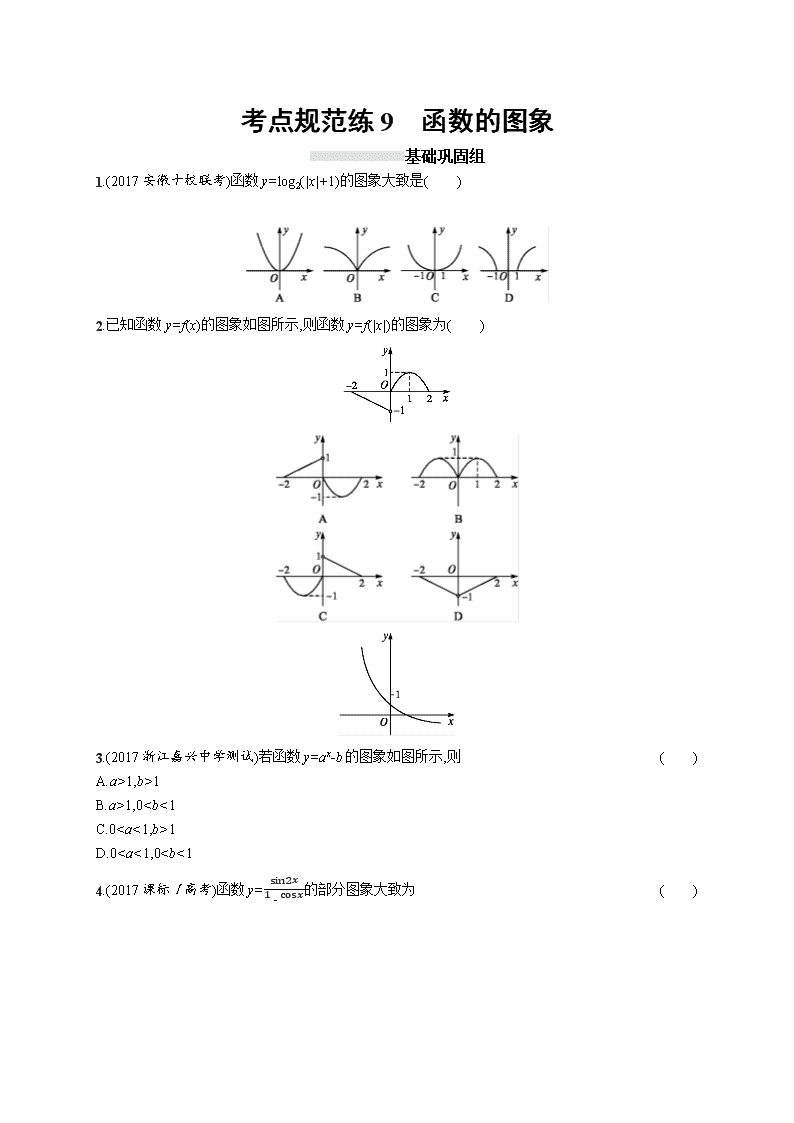
1.(2017安徽十校联考)函数y=log2(|x|+1)的图象大致是( )
2.已知函数y=f(x)的图象如图所示,则函数y=f(|x|)的图象为( )
3.(2017浙江嘉兴中学测试)若函数y=ax-b的图象如图所示,则( )
A.a>1,b>1
B.a>1,01
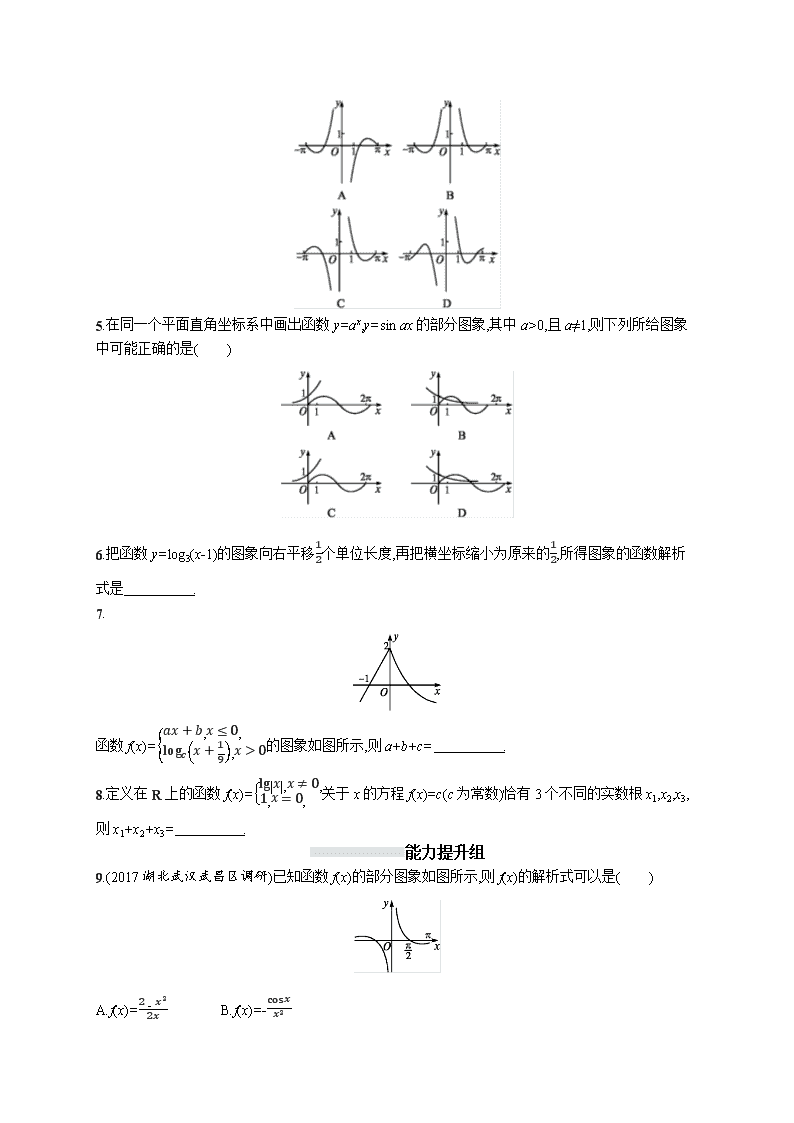
D.00,且a≠1,则下列所给图象中可能正确的是( )
6.把函数y=log3(x-1)的图象向右平移12个单位长度,再把横坐标缩小为原来的12,所得图象的函数解析式是 .
7.
函数f(x)=ax+b,x≤0,logcx+19,x>0的图象如图所示,则a+b+c= .
8.定义在R上的函数f(x)=lg|x|,x≠0,1,x=0,关于x的方程f(x)=c(c为常数)恰有3个不同的实数根x1,x2,x3,则x1+x2+x3= .
能力提升组
9.(2017湖北武汉武昌区调研)已知函数f(x)的部分图象如图所示,则f(x)的解析式可以是( )
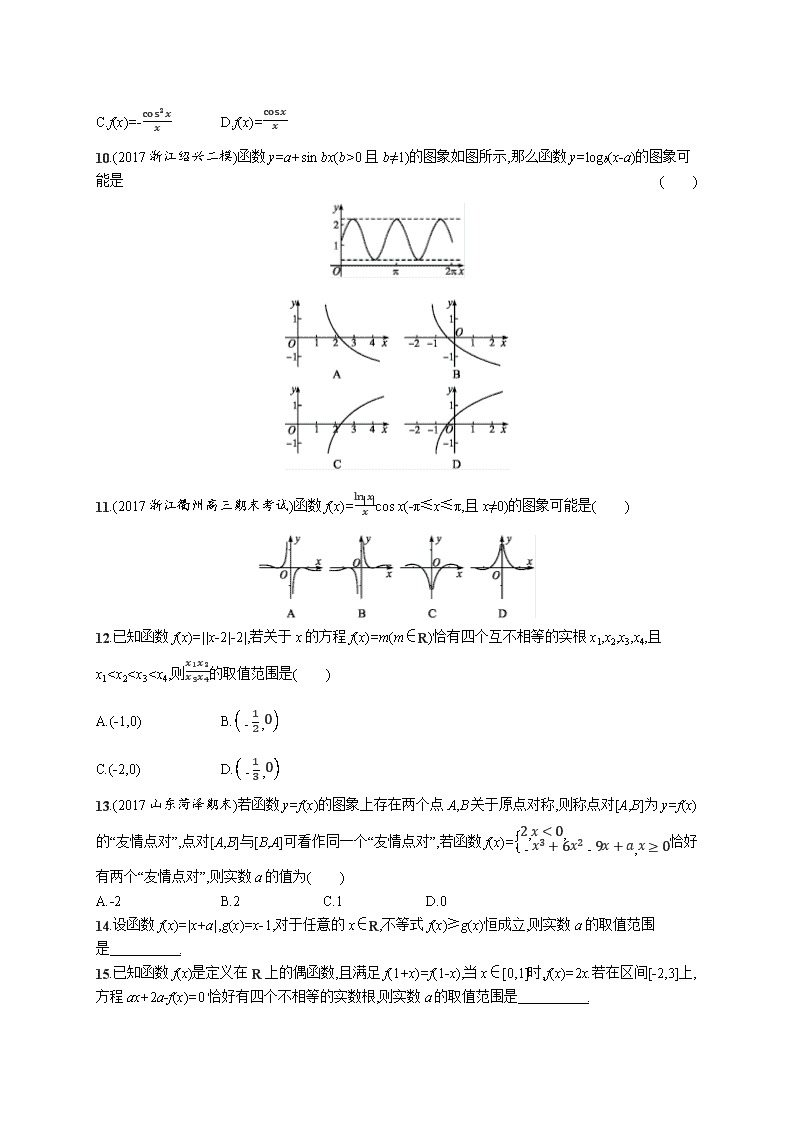
A.f(x)=2-x22x B.f(x)=-cosxx2
C.f(x)=-cos2xx D.f(x)=cosxx
10.(2017浙江绍兴二模)函数y=a+sin bx(b>0且b≠1)的图象如图所示,那么函数y=logb(x-a)的图象可能是( )
11.(2017浙江衢州高三期末考试)函数f(x)=ln|x|xcos x(-π≤x≤π,且x≠0)的图象可能是( )
12.已知函数f(x)=||x-2|-2|,若关于x的方程f(x)=m(m∈R)恰有四个互不相等的实根x1,x2,x3,x4,且x11,
(1)若对任意的x∈R,都有f(x)≤|k-1|成立,求实数k的取值范围;
(2)若存在x∈R,使|f(x)|≤k,求实数k的取值范围.
17.已知函数f(x)=x2-ax-4(a∈R)的两个零点为x1,x2,设x10时,证明:-20,而函数y=ax-b的图象是由函数y=ax的图象向下平移b个单位得到的,且函数y=ax的图象恒过点(0,b),所以由题图可知00,故排除选项A;故选C.
5.D 当a>1时,y=sin ax的周期小于2π,排除A,C.当01,且最小正周期T=2πb<π,所以b>2,则y=logb(x-a)是增函数,排除A和B;当x=2时,y=logb(2-a)<0,排除D,故选C.
11.A ∵f(-x)=ln|-x|-xcos(-x)=-ln|x|xcos x=-f(x),
∴函数f(x)为奇函数,则图象关于原点对称,故排除C,D,
当x→0时,f(x)→-∞,或者当x=π3时,fπ3=lnπ3π3×12<0故选A.
12.D 作出函数f(x)=||x-2|-2|的图象,可知图象关于直线x=2对称,则当00),则g'(x)=-3x2+12x-9=0⇒x=1或x=3,由于g(0)=g(3),所以g(1)=-a-2⇒a=2,选B.
14.
[-1,+∞) 如图作出函数f(x)=|x+a|与g(x)=x-1的图象,观察图象可知:当且仅当-a≤1,即a≥-1时,不等式f(x)≥g(x)恒成立,因此a的取值范围是[-1,+∞).
15.25,23 由f(1+x)=f(1-x)和f(x)是偶函数,得f(x+1)=f(x-1),故f(x+2)=f(x),即2为函数f(x)的一个周期.根据函数f(x)是偶函数和周期性画出函数y=f(x)在区间[-2,3]上的图象如图所示.方程ax+2a-f(x)=0恰好有四个不相等的实数根,等价于函数y=f(x)的图象与函数y=ax+2a的图象有四个不同的公共点,结合图象可得实数a满足2-02-(-3)1的图象可知,当x=12时,函数f(x)max=14,
所以|k-1|≥14,解得k≤34或k≥54.
(2)|f(x)|的图象如图所示且|f(x)|∈[0,+∞),
∵存在x∈R,使|f(x)|≤k,故k的取值范围是[0,+∞).
17.(1)证明 令f(x)=0解得x1=a-a2+162,x2=a+a2+162.
∵a2+16>a2=a,∴a-a2+162<0.
∵a>0,∴a2+16<a2+8a+16=a+4,
∴a-a2+162>a-(a+4)2=-2.
∴-20,即2x>|2x-a|(x>2).当a=0时,显然不成立,
若a>0,作出y=2x和y=|2x-a|的函数图象如图:
∴00不成立,不符合题意.
综上,a的取值范围是(0,8].