- 2.44 MB
- 2021-04-20 发布
第十九单元 算法初步、复数、推理与证明
教材复习课“算法初步、复数、推理与证明”相关基础知识一课过
算法的三种结构
[过双基]
三种基本逻辑结构
名称
内容
顺序结构
条件结构
循环结构
定 义
由若干个依次执行的步骤组成,这是任何一个算法都离不开的基本结构
算法的流程根据条件是否成立有不同的流向,条件结构就是处理这种过程的结构
从某处开始,按照一定的条件反复执行某些步骤的情况,反复执行的步骤称为循环体
程 序 框 图
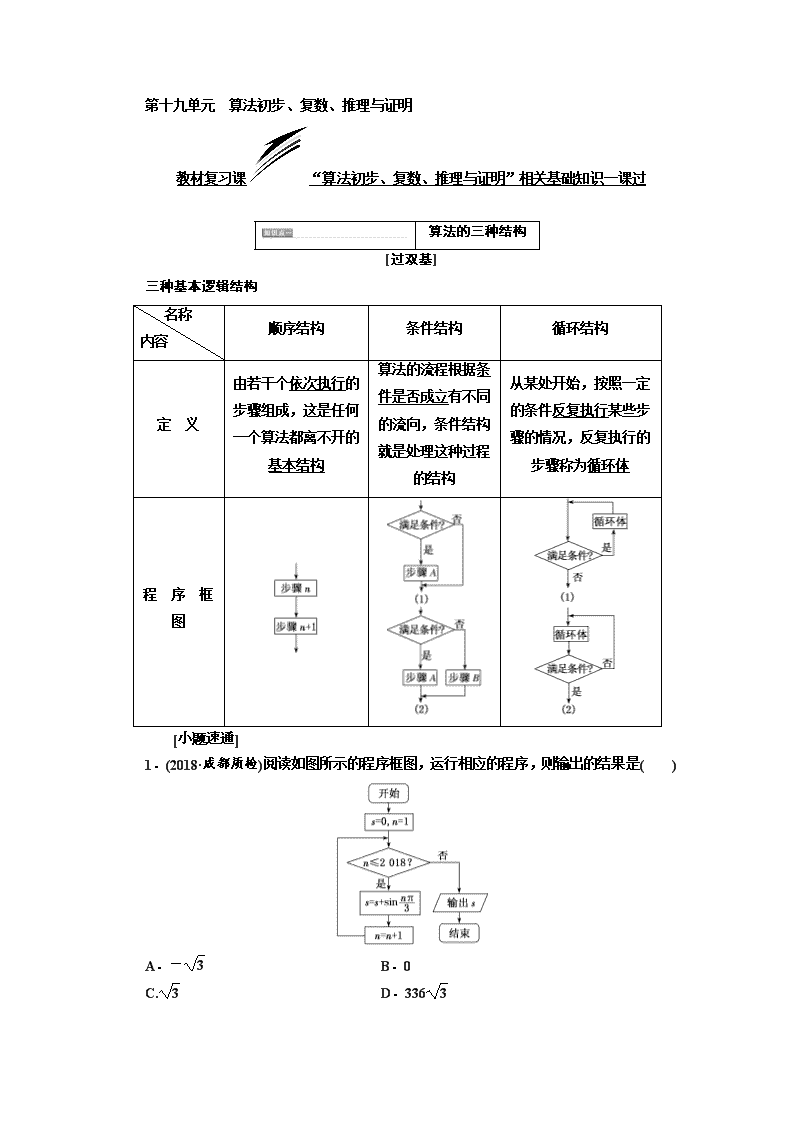
1.(2018·成都质检)阅读如图所示的程序框图,运行相应的程序,则输出的结果是( )
A.- B.0
C. D.336
解析:选C 由框图知输出的结果
s=sin+sin+…+sin,
因为函数y=sinx的周期是6,
所以s=336+sin+sin=336×0++=.
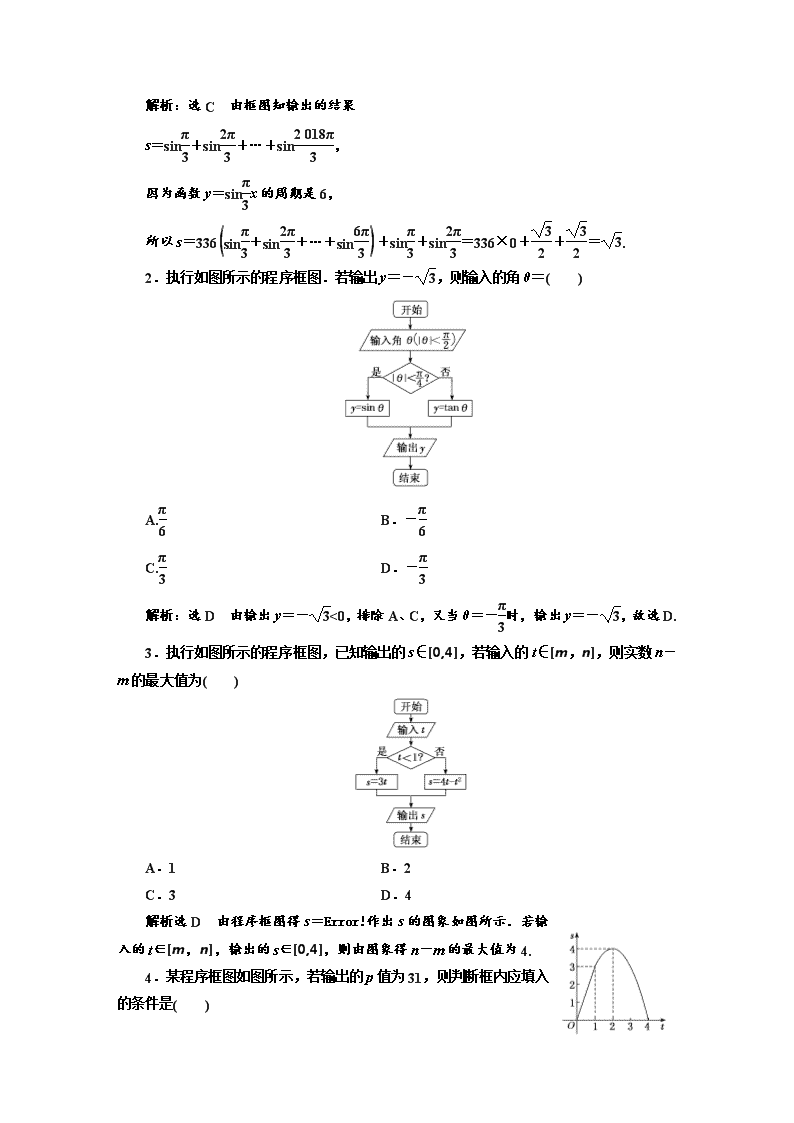
2.执行如图所示的程序框图.若输出y=-,则输入的角θ=( )
A. B.-
C. D.-
解析:选D 由输出y=-<0,排除A、C,又当θ=-时,输出y=-,故选D.
3.执行如图所示的程序框图,已知输出的s∈[0,4],若输入的t∈[m,n],则实数n-m的最大值为( )
A.1 B.2
C.3 D.4
解析:选D 由程序框图得s=作出s的图象如图所示.若输入的t∈[m,n],输出的s∈[0,4],则由图象得n-m的最大值为4.
4.某程序框图如图所示,若输出的p值为31,则判断框内应填入的条件是( )
A.n>2? B.n>3?
C.n>4? D.n>5?
解析:选B 运行程序:p=1,n=0;n=1,p=2;n=2,p=6;n=3,p=15;n=4,p=31,根据题意,此时满足条件,输出p=31,即n=3时不满足条件,n=4时满足条件,故选B.
[清易错]
1.易混淆处理框与输入框,处理框主要是赋值、计算,而输入框只是表示一个算法输入的信息.
2.易忽视循环结构中必有选择结构,其作用是控制循环进程,避免进入“死循环”,是循环结构必不可少的一部分.
某程序框图如图所示,若该程序运行后输出的值是,则a=________.
解析:由已知可得该程序的功能是计算并输出S=1+++…+
=1+1-+-+…+-
=2-.
若该程序运行后输出的值是,
则2-=, 解得a=3.
答案:3
复数的基本运算
[过双基]
1.复数的有关概念
名称
内容
备注
复数的概念
形如a+bi(a∈R,b∈R)的数叫复数,其中实部为,虚部为
若b=0,则a+bi为实数;若a=0且b≠0,则a+bi为纯虚数
复数相等
a+bi=c+di⇔a=c且b=d(a,b,c,d∈R)
共轭复数
a+bi与c+di共轭⇔a=c且b=-d(a,b,c,d∈R)
复平面
建立平面直角坐标系来表示复数的平面叫做复平面,x轴叫实轴,y轴叫虚轴
实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数,各象限内的点都表示虚数
复数的模
设对应的复数为 =a+bi,则向量的长度叫做复数 =a+bi的模
| |=|a+bi|=
2.复数的几何意义
复数集C和复平面内所有的点组成的集合是一一对应的,复数集C与复平面内所有以原点O为起点的向量组成的集合也是一一对应的,即
(1)复数 =a+bi复平面内的点 (a,b)(a,b∈R).
(2)复数 =a+bi(a,b∈R)平面向量.
3.复数的运算
设 1=a+bi, 2=c+di(a,b,c,d∈R),则
①加法: 1+ 2=(a+bi)+(c+di)=(a+c)+(b+d)i;
②减法: 1- 2=(a+bi)-(c+di)=(a-c)+(b-d)i;
③乘法: 1· 2=(a+bi)·(c+di)=(ac-bd)+(ad+bc)i;
④除法:===
(c+di≠0).
1.(2016·全国卷Ⅲ)若 =4+3i,则=( )
A.1 B.-1
C.+i D.-i
解析:选D ∵ =4+3i,∴=4-3i,| |==5,
∴==-i.
2.若复数 满足(1+i) =|+i|,则在复平面内,对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:选A 由题意,得 ===1-i,所以=1+i,其在复平面内对应的点为(1,1),位于第一象限.
3.复数(i为虚数单位)实部与虚部的和为( )
A.2 B.1
C.0 D.-2
解析:选A 因为==1+i,所以复数(i为虚数单位)实部与虚部的和为2.
4.已知(1+2i)=4+3i,则 =________.
解析:∵====2-i,
∴ =2+i.
答案:2+i
[清易错]
1.利用复数相等a+bi=c+di列方程时,注意a,b,c,d∈R的前提条件.
2.注意不能把实数集中的所有运算法则和运算性质照搬到复数集中来.例如,若 1, 2∈C, + =0,就不能推出 1= 2=0; 2<0在复数范围内有可能成立.
1.已知∈R,且m∈R,则|m+6i|=( )
A.6 B.8
C.8 D.10
解析:选D ==,
因为复数∈R,故m=8,
所以|m+6i|=|8+6i|=10.
2.已知=a+bi(a,b∈R,i为虚数单位),则a+b=______.
解析:==-1+2i,
由=a+bi,得-1+2i=a+bi,∴a=-1,b=2,
∴a+b=1.
答案:1
合情推理与演绎推理
[过双基]
1.合情推理
类型
定义
特点
归纳
推理
由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理
由部分到整体、由个别到一般
类比
推理
由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理
由特殊到特殊
2.演绎推理
(1)定义:从一般性的原理出发,推出某个特殊情况下的结论,我们把这种推理称为演绎推理.简言之,演绎推理是由一般到特殊的推理.
(2)“三段论”是演绎推理的一般模式,包括:
①大前提——已知的一般原理;
②小前提——所研究的特殊情况;
③结论——根据一般原理,对特殊情况作出的判断.
1.已知和都是无理数,试证:+也是无理数,某同学运用演绎推理证明如下:依题设和都是无理数,而无理数与无理数之和是无理数,所以+必是无理数.这个同学证明是错误的,错误原因是( )
A.大前提错误 B.小前提错误
C.推理形式错误 D.以上都可能
解析:选A 大前提:无理数与无理数之和是无理数,错误;
小前提:和都是无理数,正确;
结论:+也是无理数,正确,
故只有大前提错误.
2.我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线-=1(a>0,b>0)与x轴,直线y=h(h>0)及渐近线y=x所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积为________.
解析:由题意可知,该几何体的横截面是一个圆环,设圆环的外半径与内半径分别为R,r,
其面积S=π(R2-r2).
∵-=1⇒R2=a2+y2,
同理:r2=y2,
∴R2-r2=a2,由祖暅原理知,此旋转体的体积等价于一个半径为a,高为h的柱体的体积,为πa2h.
答案:πa2h
3.有如下等式:
以此类推,则2 018出现在第________个等式中.
解析:①2+4=6;
②8+10+12=14+16;
③18+20+22+24=26+28+30,
……
其规律为:各等式首项分别为2×1,2×(1+3),2×(1+3+5),…,
所以第n个等式的首项为2[1+3+…+(2n-1)]=2×=2n2,
当n=31时,等式的首项为2×312=1 922,
当n=32时,等式的首项为2×322=2 048,
所以2 018在第31个等式中.
答案:31
证明方法
[过双基]
1.直接证明
内容
综合法
分析法
定义
利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立
从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止
实质
由因导果
执果索因
框图表示
→→…→
→→…→
文字语言
因为……,所以……
或由……,得……
要证……,只需证……,即证……
2.间接证明
间接证明是不同于直接证明的又一类证明方法,反证法是一种常用的间接证明方法.
(1)反证法的定义:假设原命题不成立(即在原命题的条件下,结论不成立),经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立的证明方法.
(2)用反证法证明的一般步骤:
①反设——假设命题的结论不成立;
②归谬——根据假设进行推理,直到推出矛盾为止;
③结论——断言假设不成立,从而肯定原命题的结论成立.
3.数学归纳法
证明一个与正整数n有关的命题,可按下列步骤进行:
(1)(归纳奠基)证明当n取第一个值n0(n0∈N*)时命题成立;
(2)(归纳递推)假设n= ( ≥n0, ∈N*)时命题成立,证明当n= +1时命题也成立.
只要完成这两个步骤,就可以断定命题对从n0开始的所有正整数n都成立.
1.(2018·成都一模)要证a2+b2-1-a2b2≤0,只需证明( )
A.2ab-1-a2b2≤0
B.a2+b2-1-≤0
C.-1-a2b2≤0
D.(a2-1)(b2-1)≥0
解析:选D a2+b2-1-a2b2≤0⇔(a2-1)(b2-1)≥0.
2.如果命题p(n)对n= ( ∈N*)成立,则它对n= +2也成立.若p(n)对n=2也成立,则下列结论正确的是( )
A.p(n)对所有正整数n都成立
B.p(n)对所有正偶数n都成立
C.p(n)对所有正奇数n都成立
D.p(n)对所有自然数n都成立
解析:选B 由题意n= 成立,则n= +2也成立,又n=2时成立,则p(n)对所有正偶数都成立.
3.下列命题适合用反证法证明的是________.(填序号)
①已知函数f(x)=ax+(a>1),证明:方程f(x)=0没有负实数根;
②若x,y∈R,x>0,y>0,且x+y>2,
求证:和中至少有一个小于2;
③关于x的方程ax=b(a≠0)的解是唯一的;
④同一平面内,分别与两条相交直线垂直的两条直线必相交.
解析:①是“否定”型命题,②是“至少”型命题,③是“唯一”型命题,且命题中条件较少,④中条件较少,不足以直接证明,因此四个命题都适合用反证法证明.
答案:①②③④
一、选择题
1.若 =i(3-2i)(其中i为复数单位),则=( )
A.3-2i B.3+2i
C.2+3i D.2-3i
解析:选D 由 =i(3-2i)=2+3i,得=2-3i.
2.已知i为虚数单位,a为实数,复数 =在复平面上对应的点在y轴上,则a为( )
A.-3 B.-
C. D.3
解析:选A ∵ ===,
又复数 =在复平面上对应的点在y轴上,
∴解得a=-3.
3.分析法又称执果索因法,若用分析法证明“设a>b>c,且a+b+c=0,求证:0 B.a-c>0
C.(a-b)(a-c)>0 D.(a-b)(a-c)<0
解析:选C 0⇔(a-c)(2a+c)>0
⇔(a-c)(a-b)>0.
4.利用数学归纳法证明“(n+1)(n+2)·…·(n+n)=2n×1×3×…×(2n-1),n∈N*”时,从“n= ”变到“n= +1”时,左边应增乘的因式是( )
A.2 +1 B.2(2 +1)
C. D.
解析:选B 当n= ( ∈N*)时,
左式为( +1)( +2) ·…·( + );
当n= +1时,左式为( +1+1)( +1+2)·…·( +1+ -1)( +1+ )( +1+ +1),
则左边应增乘的式子是=2(2 +1).
5.(2017·北京高考)执行如图所示的程序框图,输出的s值为( )
A.2 B.
C. D.
解析:选C 运行该程序, =0,s=1, <3;
=0+1=1,s==2, <3;
=1+1=2,s==, <3;
=1+2=3,s==,此时不满足循环条件,输出s,故输出的s值为.
6.若数列{an}是等差数列,bn=,则数列{bn}也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )
A.dn=
B.dn=
C.dn=
D.dn=
解析:选D 因为数列{an}是等差数列,所以bn==a1+(n-1)·(d为等差数列{an}的公差),{bn}也为等差数列,因为正项数列{cn}是等比数列,设公比为q,则dn===c1q,所以{dn}也是等比数列.
7.执行如图所示的程序框图,若输出的结果是,则判断框内应填的内容是( )
A.n<98? B.n<99?
C.n<100? D.n<101?
解析:选B 由==-,
可知程序框图的功能是计算并输出S=++…+==的值.
由题意令=,解得n=99,
即当n<99时,执行循环体,若不满足此条件,则退出循环,输出S的值.
8.已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个“整数对”是( )
A.(7,5) B.(5,7)
C.(2,10) D.(10,1)
解:选B 依题意,把“整数对”的和相同的分为一组,不难得知第n组中每个“整数对”的和均为n+1,且第n组共有n个“整数对”,这样的前n组一共有个“整数对”,注意到<60<,因此第60个“整数对”处于第11组(每个“整数对”的和为12的组)的第5个位置,结合题意可知每个“整数对”的和为12的组中的各对数依次为:(1,11),(2,10),(3,9),(4,8),(5,7),…,因此第60个“整数对”是(5,7).
二、填空题
9.M=+++…+与1的大小关系为__________.
解析:因为M=+++…+
=+++…+
<+++…+=1,
所以M<1.
答案:M<1
10.若复数 =(其中i为虚数单位)的实部与虚部相等,则实数a=________.
解析:因为复数 ===1-ai,
所以-a=1,即a=-1.
答案:-1
11.下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=________.
解析:a=14,b=18.
第一次循环:14≠18且14<18,b=18-14=4;
第二次循环:14≠4且14>4,a=14-4=10;
第三次循环:10≠4且10>4,a=10-4=6;
第四次循环:6≠4且6>4,a=6-4=2;
第五次循环:2≠4且2<4,b=4-2=2;
第六次循环:a=b=2,跳出循环,输出a=2.
答案:2
12.设n为正整数,f(n)=1+++…+,计算得f(2)=,f(4)>2,f(8)>,f(16)>3,观察上述结果,可推测一般的结论为________.
解析:∵f(21)=,f(22)>2=,
f(23)>,f(24)>,
∴归纳得f(2n)≥(n∈N*).
答案:f(2n)≥(n∈N*)
三、解答题
13.若a>b>c>d>0且a+d=b+c,
求证:+<+.
证明:要证+<+,
只需证(+)2<(+)2,
即证a+d+2<b+c+2,
因为a+d=b+c,所以只需证<,即证ad<bc,
设a+d=b+c=t,
则ad-bc=(t-d)d-(t-c)c=(c-d)(c+d-t)<0,
故ad<bc成立,从而+<+成立.
14.等差数列{an}的前n项和为Sn,a1=1+,S3=9+3.
(1)求数列{an}的通项an与前n项和Sn;
(2)设bn=(n∈N*),求证:数列{bn}中任意不同的三项都不可能成为等比数列.
解:(1)由已知得
所以d=2,故an=2n-1+,Sn=n(n+).
(2)证明:由(1),得bn==n+.假设数列{bn}中存在三项bp,bq,br(p,q,r互不相等)成等比数列,
则b=bpbr,即(q+)2=(p+)(r+),
所以(q2-pr)+(2q-p-r)=0.
因为p,q,r∈N*,所以
所以2=pr,(p-r)2=0.
所以p=r,这与p≠r矛盾,所以数列{bn}中任意不同的三项都不可能成为等比数列.
高考研究课(一)
算法与程序框图考查2类型——推结果、填条件
[全国卷5年命题分析]
考点
考查频度
考查角度
循环结构
5年10考
循环结构程序框图的输出功能及应用
程序框图补条件
5年1考
补全满足框图的条件
程序框图的推结果问题
[典例] (1)(2017·全国卷Ⅱ)执行如图所示的程序框图,如果输入的a=-1,则输出的S=( )
A.2 B.3
C.4 D.5
(2)(2017·山东高考)执行两次如图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为( )
A.0,0 B.1,1
C.0,1 D.1,0
[解析] (1)运行程序框图,
a=-1,S=0, =1, ≤6成立;
S=0+(-1)×1=-1,a=1, =2, ≤6成立;
S=-1+1×2=1,a=-1, =3, ≤6成立;
S=1+(-1)×3=-2,a=1, =4, ≤6成立;
S=-2+1×4=2,a=-1, =5, ≤6成立;
S=2+(-1)×5=-3,a=1, =6, ≤6成立;
S=-3+1×6=3,a=-1, =7, ≤6不成立,输出S=3.
(2)当输入x=7时,b=2,因为b2>x不成立且x不能被b整除,故b=3,这时b2>x成立,故a=1,输出a的值为1.
当输入x=9时,b=2,因为b2>x不成立且x不能被b整除,故b=3,这时b2>x不成立且x能被b整除,故a=0,输出a的值为0.
[答案] (1)B (2)D
[方法技巧]
解决程序框图推结果问题要注意几个常用变量
(1)计数变量:用来记录某个事件发生的次数,如i=i+1.
(2)累加变量:用来计算数据之和,如S=S+i.
(3)累乘变量:用来计算数据之积,如p=p×i.
[即时演练]
1.(2016·全国卷Ⅰ)执行如图所示的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足( )
A.y=2x B.y=3x
C.y=4x D.y=5x
解析:选C 输入x=0,y=1,n=1,
运行第一次,x=0,y=1,不满足x2+y2≥36;
运行第二次,x=,y=2,不满足x2+y2≥36;
运行第三次,x=,y=6,满足x2+y2≥36,
输出x=,y=6.由于点在直线y=4x上,故选C.
2.执行如图所示的程序框图,输出的s是________.
解析:第一次循环:i=1,s=1;第二次循环:i=2,s=-1;第三次循环:i=3,s=2;第四次循环:i=4,s=-2,此时i=5,执行s=3×(-2)=-6,故输出s=-6.
答案:-6
程序框图的补全及逆向求解问题
[典例] (1)《九章算术》是中国古代数学名著,体现了古代劳动人民数学的智慧,其中第六章“均输”中,有一竹节容量问题,某教师根据这一问题的思想设计了如图所示的程序框图,若输出的m的值为35,则输入的a的值为( )
A.4 B.5
C.7 D.11
(2)一个算法的程序框图如图所示,该程序输出的结果为,则空白处应填入的条件为( )
A.i≤9? B.i≤6?
C.i≥9? D.i≤8?
[解析] (1)起始阶段有m=2a-3,i=1,
第一次循环:m=2×(2a-3)-3=4a-9,i=2,
第二次循环:m=2×(4a-9)-3=8a-21,i=3,
第三次循环:m=2×(8a-21)-3=16a-45,i=4,
第四次循环:m=2×(16a-45)-3=32a-93,
跳出循环,输出m=32a-93=35,解得a=4.
(2)由=及题意知,该程序框图的功能是计算S=1-+-+…+-+-=-+的值,由S=,得i=9.
故空白处应填入的条件为:i≤9.
[答案] (1)A (2)A
[方法技巧]
程序框图的补全及逆向求解问题
(1)先假设参数的判断条件满足或不满足;
(2)运行循环结构,一直到运行结果与题目要求的输出结果相同为止;
(3)根据此时各个变量的值,补全程序框图.
[即时演练]
1.执行如图所示的程序框图,若输出 的值为16,则判断框内可填入的条件是( )
A.S<? B.S>?
C.S>? D.S<?
解析:选D 运行程序: =10,S=1;S=, =11;S=, =12;S=, =13;S=, =14;S=, =15;S==, =16,此时不满足条件,循环结束,输出 =16,所以判断框内可填入条件是S<?.
2.运行如图所示的程序框图,若输出的y值的范围是[0,10],则输入的x值的范围是________.
解析:该程序的功能是计算分段函数的值,
y=
当x<-1时,由0≤3-x≤10,可得-7≤x<-1;
当-1≤x≤1时,0≤x2≤10成立;
当x>1时,由0≤x+1≤10,可得1<x≤9,
综上,输入的x值的范围是[-7,9].
答案:[-7,9]
1.(2017·全国卷Ⅰ)如图所示的程序框图是为了求出满足3n-2n>1 000的最小偶数n,那么在◇和▭两个空白框中,可以分别填入( )
A.A>1 000和n=n+1
B.A>1 000和n=n+2
C.A≤1 000和n=n+1
D.A≤1 000和n=n+2
解析:选D 程序框图中A=3n-2n,且判断框内的条件不满足时输出n,所以判断框中应填入A≤1 000,由于初始值n=0,要求满足A=3n-2n>1 000的最小偶数,故执行框中应填入n=n+2.
2.(2017·全国卷Ⅲ)执行如图所示的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )
A.5 B.4
C.3 D.2
解析:选D 执行程序框图,S=0+100=100,M=-10,t=2;S=100-10=90,M=1,t=3,S<91,输出S,此时,t=3不满足t≤N,所以输入的正整数N的最小值为2.
3.(2016·全国卷Ⅱ)中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )
A.7 B.12
C.17 D.34
解析:选C 第一次运算:s=0×2+2=2, =1;
第二次运算:s=2×2+2=6, =2;
第三次运算:s=6×2+5=17, =3>2,
结束循环,s=17.
4.(2016·全国卷Ⅲ)执行如图所示的程序框图,如果输入的a=4,b=6,那么输出的n=( )
A.3 B.4
C.5 D.6
解析:选B 程序运行如下:
开始a=4,b=6,n=0,s=0.
第1次循环:a=2,b=4,a=6,s=6,
n=1;
第2次循环:a=-2,b=6,a=4,
s=10,n=2;
第3次循环:a=2,b=4,a=6,s=16,
n=3;
第4次循环:a=-2,b=6,a=4,
s=20,n=4.
此时,满足条件s>16,
退出循环,输出n=4.故选B.
5.(2015·全国卷Ⅰ)执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )
A.5 B.6
C.7 D.8
解析:选C 运行第一次:S=1-==0.5,m=0.25,n=1,S>0.01;
运行第二次:S=0.5-0.25=0.25,m=0.125,n=2,S>0.01;
运行第三次:S=0.25-0.125=0.125,m=0.062 5,n=3,S>0.01;
运行第四次:S=0.125-0.062 5=0.062 5,m=0.031 25,n=4,S>0.01;
运行第五次:S=0.031 25,m=0.015 625,n=5,S>0.01;
运行第六次:S=0.015 625,m=0.007 812 5,n=6,S>0.01;
运行第七次:S=0.007 812 5,m=0.003 906 25,n=7,S<0.01.
输出n=7.故选C.
6.(2014·全国卷Ⅰ)执行如图所示程序框图,若输入的a,b, 分别为1,2,3,则输出的M=( )
A. B.
C. D.
解析:选D 第一次循环:M=,a=2,b=,n=2;
第二次循环:M=,a=,b=,n=3;
第三次循环:M=,a=,b=,n=4.
则输出M=.
7.(2014·全国卷Ⅱ)执行如图的程序框图,如果输入的x,t均为2,则输出的S=( )
A.4 B.5
C.6 D.7
解析:选D 执行循环体,
第一次循环,M=2,S=5, =2;
第二次循环,M=2,S=7, =3.
故输出的S=7.
一、选择题
1.(2017·山东高考)执行如图所示的程序框图,当输入的x的值为4时,输出的y的值为2,则空白判断框中的条件可能为( )
A.x>3 B.x>4
C.x≤4 D.x≤5
解析:选B 当x=4时,若执行“是”,则y=4+2=6,与题意矛盾;若执行“否”,则y=log24=2,满足题意,故应执行“否”.故判断框中的条件可能为x>4.
2.执行如图所示的程序框图,若输入的a的值为2,则输出的b的值为( )
A.-2 B.1 C.2 D.4
解析:选A 第一次循环,a=,b=1,i=2;第二次循环,a=-1,b=-2,i=3;第三次循环,a=2,b=4,i=4;第四次循环,a=,b=1,i=5;……;由此可知b的值以3为周期出现,且当i=2 019时退出循环,此时共循环2 018次,又2 018=3×672+2,所以输出的b的值为-2.
3.某班有50名学生,在一次数学考试中,an表示学号为n
的学生的成绩,则执行如图所示的程序框图,下列结论正确的是( )
A.P表示成绩不高于60分的人数
B.Q表示成绩低于80分的人数
C.R表示成绩高于80分的人数
D.Q表示成绩不低于60分,且低于80分的人数
解析:选D P表示成绩低于60分的人数,Q表示成绩低于80分且不低于60分的人数,R表示成绩不低于80分的人数.
4.(2017·天津高考)阅读如图所示的程序框图,运行相应的程序,若输入N的值为24,则输出N的值为( )
A.0 B.1
C.2 D.3
解析:选C 第一次循环,24能被3整除,N==8>3;
第二次循环,8不能被3整除,N=8-1=7>3;
第三次循环,7不能被3整除,N=7-1=6>3;
第四次循环,6能被3整除,N==2<3,结束循环,
故输出N的值为2.
5.执行如图所示的程序框图,则输出S的值为( )
A.3 B.-6
C.10 D.-15
解析:选D 第一次执行程序,得到S=0-12=-1,i=2;
第二次执行程序,得到S=-1+22=3,i=3;
第三次执行程序,得到S=3-32=-6,i=4;
第四次执行程序,得到S=-6+42=10,i=5;
第五次执行程序,得到S=10-52=-15,i=6,
结束循环,输出的S=-15.
6.某校为了了解高三学生日平均睡眠时间(单位:h),随机选择了50位学生进行调查.下表是这50位同学睡眠时间的频率分布表:
组别(i)
睡眠时间
组中值( i)
频数
频率(Pi)
1
[4.5,5.5)
5
2
0.04
2
[5.5,6.5)
6
6
0.12
3
[6.5,7.5)
7
20
0.40
4
[7.5,8.5)
8
18
0.36
5
[8.5,9.5)
9
3
0.06
6
[9.5,10.5)
10
1
0.02
现根据如下程序框图用计算机统计平均睡眠时间,则判断框①中应填入的条件是( )
A.i>4? B.i>5?
C.i>6? D.i>7?
解析:选B 根据题目中程序框图,用计算机统计平均睡眠时间,总共执行6次循环,则判断框①中应填入的条件是i>5(或i≥6?).
7.下图为某一函数的求值程序框图,根据框图,如果输出y的值为3,那么应输入x=( )
A.1 B.2
C.3 D.6
解析:选B 该程序的作用是计算分段函数y=的函数值,
由题意,若x>6,则当y=3时,x-3=3,解得x=6,舍去;
若x≤2,则当y=3时,5-x=3,解得x=2,
故输入的x值为2.
8.给出30个数:1,2,4,7,…,其规律是:第1个数是1;第2个数比第1个数大1;第3个数比第2个数大2;第4个数比第3个数大3,…,以此类推,要计算这30个数的和,现已给出了该问题的程序框图如图所示,那么框图中判断框①处和执行框②处应分别填入( )
A.i≤30?;p=p+i-1
B.i≤29?;p=p+i+1
C.i≤31?;p=p+i
D.i≤30?;p=p+i
解析:选D 由于要计算30个数的和,故循环要执行30次,由于循环变量的初值为1,步长为1,故①中应填写“i≤30?”.又由第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,故②中应填p=p+i.
二、填空题
9.(2017·江苏高考)如图是一个算法流程图.若输入x的值为,则输出y的值是________.
解析:由流程图可知其功能是运算分段函数y=所以当输入的x的值为时,y=2+log2=2-4=-2.
答案:-2
10.按下列程序框图来计算:
如果输入的x=5,则应该运算________次才停止.
解析:由题意,该程序按如下步骤运行:
经过第一次循环得到x=3×5-2=13,不满足x>200,进入下一步循环;
经过第二次循环得到x=3×13-2=37,不满足x>200,进入下一步循环;
经过第三次循环得到x=3×37-2=109,不满足x>200,进入下一步循环;
经过第四次循环得到x=3×109-2=325,因为325>200,结束循环并输出x的值
因此,运算进行了4次后,输出x值而程序停止.故答案为4.
答案:4
11.中国古代有计算多项式值的秦九韶算法,该算法的程序框图如图所示. 执行该程序框图,若输入的x=3,n=3,输入的a依次为由小到大顺序排列的质数(从最小质数开始),直到结束为止,则输出的s=________.
解析:运行程序:
x=3,n=3, =0,s=0;a=2,s=2, =1;a=3,s=9, =2;a=5,s=32, =3;a=7,s=103, =4,此时满足条件,循环结束,输出s=103.
答案:103
12.阅读如图所示的程序框图,运行相应的程序,输出的结果是a=________.
解析:运行程序,可得a=10,i=1,不满足i≥5,不满足a是奇数,a=5,i=2,不满足i≥5,满足a是奇数,a=16,i=3,不满足i≥5,不满足a是奇数,a=8,i=4,不满足i≥5,不满足a是奇数,a=4,i=5,满足i≥5,退出循环,输出a的值为4.
答案:4
13.已知某程序框图如图所示,则程序运行结束时输出的结果为________.
解析:第一次循环结束时,n=2,x=3,y=1;
第二次循环结束时,n=4,x=9,y=3;
第三次循环结束时,n=6,x=27,y=3.
此时满足n>4,
结束循环,输出logyx=log327=3.
答案:3
14.(2018·黄山调研)我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=________.
解析:第一次循环,得S=2;第二次循环,得n=2,a=,A=2,S=;第三次循环,得n=3,a=,A=4,S=;第四次循环,得n=4,a=,A=8,S=>10,结束循环,输出的n=4.
答案:4
1.图1是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次是A1,A2,…,A16
,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )
图1
图2
A.6 B.7 C.10 D.16
解析:选C 由程序框图可知,其统计的是数学成绩大于等于90的人数,
所以由茎叶图知,数学成绩大于等于90的人数为10,
因此输出结果为10.
2.如果执行程序框图,如果输出的S=2 550,则判断框内应填入的条件是( )
A. ≤50? B. ≥51?
C. <50? D. >51?
解析:选A 根据题中的程序框图,可得
该程序经过第一次循环得到S=2, =2;
经过第二次循环得到S=2+4, =3;
经过第三次循环得到S=2+4+6, =4;
……
设经过第n次循环得到2+4+6+…+2n=n2+n=2 550,
解得n=50,
由此说明,当n>50时不满足判断框中的条件,则正好输出S=2 550,
∴判断框应填入的条件是 ≤50?.
高考研究课(二)
数系的扩充与复数的引入的命题3角度——概念、运算、意义
[全国卷5年命题分析]
考点
考查频度
考查角度
复数的有关概念
5年4考
虚部、模等有关概念与运算结合考查
复数的几何意义
5年2考
与运算结合考查几何意义
复数的运算
5年6考
考查乘法、除法、幂的运算
复数的有关概念
[典例] (1)设i是虚数单位.若复数a-(a∈R)是纯虚数,则a的值为( )
A.-3 B.-1
C.1 D.3
(2)已知复数 满足=|2-i|,则 的共轭复数对应的点位于复平面内的( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
(3)若复数 满足 (1+i)=2i(i为虚数单位),则| |=( )
A.1 B.2
C. D.
[解析] (1)∵复数a-=a-=(a-3)-i为纯虚数,∴a-3=0,∴a=3.
(2)∵=|2-i|=,∴ =+i,
则 的共轭复数-i对应的点(,-)位于复平面内的第四象限.
(3)法一:设 =a+bi(a,b∈R),则由 (1+i)=2i,得(a+bi)·(1+i)=2i,所以(a-b)+(a+b)i=2i,由复数相等的条件得解得a=b=1,所以 =1+i,故| |==.
法二:由 (1+i)=2i,得 ===i-i2=1+i,所以| |==.
[答案] (1)D (2)D (3)C
[方法技巧]
求解与复数概念相关问题的技巧
复数的分类、复数的相等、复数的模,共轭复数的概念都与复数的实部与虚部有关,所以解答与复数相关概念有关的问题时,需把所给复数化为代数形式,即a+bi(a,b∈R)的形式,再根据题意求解.
[即时演练]
1.(2017·山东高考)已知a∈R,i是虚数单位.若 =a+ i, ·=4,则a=( )
A.1或-1 B.或-
C.- D.
解析:选A 法一:由题意可知=a-i,
∴ ·=(a+i)(a-i)=a2+3=4,故a=1或-1.
法二: ·=| |2=a2+3=4,故a=1或-1.
2.若复数(a∈R)是纯虚数(i是虚数单位),则复数 =a+(a-3)i在复平面内对应的点位于第________象限.
解析:∵===+i是纯虚数,
∴解得a=2.
∴ =2-i,在复平面内对应的点(2,-1)位于第四象限.
答案:四
3.(2017·浙江高考)已知a,b∈R,(a+bi)2=3+4i(i是虚数单位),则a2+b2=________,ab=________.
解析:∵(a+bi)2=a2-b2+2abi=3+4i,
∴∴或
∴a2+b2=5,ab=2.
答案:5 2
复数的代数运算
[典例] (1)i为虚数单位,则2 018=( )
A.-i B.-1
C.i D.1
(2)(2017·全国卷Ⅱ)=( )
A.1+2i B.1-2i
C.2+i D.2-i
(3)(2017·全国卷Ⅱ)(1+i)(2+i)=( )
A.1-i B.1+3i
C.3+i D.3+3i
[解析] (1)∵===-i,
∴2 018=(-i)2 018
=(-i)2 016·(-i)2=-1.
(2)===2-i.
(3)(1+i)(2+i)=2+i2+3i=1+3i.
[答案] (1)B (2)D (3)B
[方法技巧]
复数代数形式运算问题的解题策略
(1)复数的乘法
复数的乘法类似于多项式的四则运算,可将含有虚数单位i的看作一类同类项,不含i的看作另一类同类项,分别合并即可.
(2)复数的除法
除法的关键是分子分母同乘以分母的共轭复数,解题中要注意把i的幂写成最简形式.
[提醒] 在进行复数的代数运算时,记住以下结论,可提高计算速度.
(1)(1±i)2=±2i;=i;=-i;
(2)-b+ai=i(a+bi);
(3)i4n=1,i4n+1=i,i4n+2=-1,i4n+3=-i,
i4n+i4n+1+i4n+2+i4n+3=0,n∈N*.
[即时演练]
1.设复数 =1+i(i是虚数单位),则+ 2=( )
A.1+i B.1-i
C.-1-i D.-1+i
解析:选A + 2=+(1+i)2=1-i+2i=1+i.
2.已知复数 =,是 的共轭复数,则 ·=________.
解析:∵ ==
=
=
==-+i,
故=--i,
∴ ·==+=.
答案:
3.已知i是虚数单位,2 018+6=________.
解析:原式=1 009+6=1 009+i6=i1 009+i6=i4×252+1+i4+2=i+i2=-1+i.
答案:-1+i
复数的几何意义
[典例] (1)已知复数 =a+i(a∈R).若| |<,则 +i2在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
(2)(2017·北京高考)若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是( )
A.(-∞,1) B.(-∞,-1)
C.(1,+∞) D.(-1,+∞)
[解析] (1)因为复数 =a+i(a∈R).若| |<,则<,解得-1<a<1,所以 +i2=a-1+i在复平面内对应的点(a-1,1)位于第二象限.
(2)复数(1-i)(a+i)=a+1+(1-a)i,
其在复平面内对应的点(a+1,1-a)在第二象限,
故解得a<-1.
[答案] (1)B (2)B
[方法技巧]
(1)复数 、复平面上的点 及向量相互联系,即 =a+bi(a,b∈R)⇔ (a,b)⇔.
(2)由于复数、点、向量之间建立了一一对应的关系,因此可把复数、向量与解析几何联系在一起,解题时可运用数形结合的方法,使问题的解决更加直观.
[即时演练]
1.如图,若向量对应的复数为 ,则 +表示的复数为( )
A.1+3i
B.-3-i
C.3-i
D.3+i
解析:选D 由图可得 (1,-1),即 =1-i,所以 +=1-i+=1-i+=1-i+=1-i+2+2i=3+i.
2.若 =(a-2)+(a+1)i在复平面内对应的点在第二象限,则实数a的取值范围是________.
解析:∵ =(a-2)+(a+1)i在复平面内对应的点在第二象限,
∴解得-1<a<2.
即实数a的取值范围是(-1,2).
答案:(-1,2)
1.(2017·全国卷Ⅰ)设有下面四个命题:
p1:若复数 满足∈R,则 ∈R;
p2:若复数 满足 2∈R,则 ∈R;
p3:若复数 1, 2满足 1 2∈R,则 1=2;
p4:若复数 ∈R,则∈R.
其中的真命题为( )
A.p1,p3 B.p1,p4
C.p2,p3 D.p2,p4
解析:选B 设复数 =a+bi(a,b∈R),对于p1,∵==∈R,∴b=0,∴ ∈R,∴p1是真命题;
对于p2,∵ 2=(a+bi)2=a2-b2+2abi∈R,∴ab=0,∴a=0或b=0,∴p2不是真命题;
对于p3,设 1=x+yi(x,y∈R), 2=c+di(c,d∈R),则 1 2=(x+yi)(c+di)=cx-dy+(dx
+cy)i∈R,
∴dx+cy=0,取 1=1+2i, 2=-1+2i, 1≠2,
∴p3不是真命题;
对于p4,∵ =a+bi∈R,∴b=0,∴=a-bi=a∈R,
∴p4是真命题.
2.(2017·全国卷Ⅲ)复平面内表示复数 =i(-2+i)的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:选C =i(-2+i)=-2i+i2=-1-2i,故复平面内表示复数 =i(-2+i)的点位于第三象限.
3.(2016·全国卷Ⅰ)设(1+i)x=1+yi,其中x,y是实数,则|x+yi|=( )
A.1 B.
C. D.2
解析:选B ∵(1+i)x=1+yi,∴x+xi=1+yi.
又∵x,y∈R,∴x=1,y=1.
∴|x+yi|=|1+i|=.
4.(2016·全国卷Ⅱ)已知 =(m+3)+(m-1)i在复平面内对应的点在第四象限,则实数m的取值范围是( )
A.(-3,1) B.(-1,3)
C.(1,+∞) D.(-∞,-3)
解析:选A 由题意知即-30),
则两边平方得,则3+2=m2,
即3+2m=m2,解得m=3或m=-1(舍去).
2.在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外接圆面积为S2,则=,推广到空间可以得到类似结论:已知正四面体PABC的内切球体积为V1,外接球体积为V2,则=( )
A. B.
C. D.
解析:选D 正四面体的内切球与外接球的半径之比为1∶3,故=.
归纳推理
[典例] (1)在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2,3,4,…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=________;f(n)=________(答案用n表示).
(2)(2016·山东高考)观察下列等式:
-2+-2=×1×2;
-2+-2+-2+-2=×2×3;
-2+-2+-2+…+-2=×3×4;
-2+-2+-2+…+-2=×4×5;
……
照此规律,
-2+-2+-2+…+-2=________.
[解析] (1)由题意知,f(1)=1,f(2)=1+1+2,f(3)=1+1+2+1+2+3,…,
f(n)=1+1+2+1+2+3+…+1+2+3+…+n,
分析可得:f(n)-f(n-1)=1+2+3+…+n==+;
f(n)=[f(n)-f(n-1)]+[f(n-1)-f(n-2)]+[f(n-2)-f(n-3)]+…+f(2)-f(1)+f(1)
=(12+22+32+…+n2)+(1+2+3…+n)=n(n+1)(2n+1)+n(n+1)=n(n+1)(n+2).
(2)通过观察已给出等式的特点,可知等式右边的是个固定数,后面第一个数是等式左边最后一个数括号内角度值分子中π的系数的一半,后面第二个数是第一个数的下一个自然数,所以,所求结果为×n×(n+1),即n(n+1).
[答案] (1)10 n(n+1)(n+2) (2)n(n+1)
[方法技巧]
归纳推理问题的常见类型及解题策略
常见类型
解题策略
与数字有关的等式的推理
观察数字特点,找出等式左右两侧的规律及符号可解
与式子有关的推理
观察每个式子的特点,找到规律后可解
与图形变化有关的推理
合理利用特殊图形归纳推理得出结论,并用赋值检验法验证其真伪性
[即时演练]
1.观察下列等式:
12=1;
12-22=-3;
12-22+32=6;
12-22+32-42=-10;
……
照此规律,第n个等式为________________.
解析:观察规律可知,第n个式子为12-22+32-42+…+(-1)n+1n2=(-1)n+1.
答案:12-22+32-42+…+(-1)n+1n2=(-1)n+1
2.已知结论“a1,a2∈R+,且a1+a2=1,则+≥4;若a1,a2,a3∈R+,且a1+a2+a3=1,则++≥9”,请猜想若a1,a2,…,an∈R+,且a1+a2+…+an=1,则++…+≥________.
解析:由题意知,结论左端各项分别是和为1的各数ai的倒数(i=1,2,…,n),
右端n=2时为4=22,n=3时为9=32,
故ai∈R+,a1+a2+…+an=1时,结论为++…+≥n2(n≥2).
答案:n2
演绎推理
[典例] 数列{an}的前n项和记为Sn,已知a1=1,an+1=Sn(n∈N*).证明:
(1)数列是等比数列;
(2)Sn+1=4an.
[证明] (1)∵an+1=Sn+1-Sn,an+1=Sn,
∴(n+2)Sn=n(Sn+1-Sn),
即nSn+1=2(n+1)Sn.
故=2·,(小前提)
故是以1为首项,2为公比的等比数列.(结论)
(大前提是等比数列的定义)
(2)由(1)可知=4·(n≥2),
∴Sn+1=4(n+1)·=4··Sn-1
=4an(n≥2).(小前提)
又∵a2=3S1=3,S2=a1+a2=1+3=4=4a1,(小前提)
∴对于任意正整数n,都有Sn+1=4an.(结论)
[方法技巧]
演绎推理的推理过程中的2个注意点
(1)演绎推理是从一般到特殊的推理,其一般形式是三段论,应用三段论解决问题时,应当首先明确什么是大前提和小前提,如果前提是显然的,则可以省略,本题中,等比数列的定义在解题中是大前提,由于它是显然的,因此省略不写.
(2)在推理论证过程中,一些稍复杂一点的证明题常常要由几个三段论才能完成.
[即时演练]
已知函数y=f(x)满足:对任意a,b∈R,a≠b,都有af(a)+bf(b)>af(b)+bf(a),试证明:f(x)为R上的单调增函数.
证明:设x1,x2∈R,取x1x1f(x2)+x2f(x1),
∴x1[f(x1)-f(x2)]+x2[f(x2)-f(x1)]>0,
[f(x2)-f(x1)](x2-x1)>0,
∵x10,f(x2)>f(x1).
∴y=f(x)为R上的单调增函数.
1.(2017·全国卷Ⅱ)甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( )
A.乙可以知道四人的成绩
B.丁可以知道四人的成绩
C.乙、丁可以知道对方的成绩
D.乙、丁可以知道自己的成绩
解析:
选D 依题意,四人中有2位优秀,2位良好,由于甲知道乙、丙的成绩,但还是不知道自己的成绩,则乙、丙必有1位优秀,1位良好,甲、丁必有1位优秀,1位良好,因此,乙知道丙的成绩后,必然知道自己的成绩;丁知道甲的成绩后,必然知道自己的成绩,因此选D.
2.(2016·北京高考)袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则( )
A.乙盒中黑球不多于丙盒中黑球
B.乙盒中红球与丙盒中黑球一样多
C.乙盒中红球不多于丙盒中红球
D.乙盒中黑球与丙盒中红球一样多
解析:选B 法一:取两个球往盒子中放有4种情况:
①红+红,则乙盒中红球数加1;
②黑+黑,则丙盒中黑球数加1;
③红+黑(红球放入甲盒中),则乙盒中黑球数加1;
④黑+红(黑球放入甲盒中),则丙盒中红球数加1.
因为红球和黑球个数一样多,所以①和②的情况一样多,
③和④的情况完全随机.
③和④对B选项中的乙盒中的红球数与丙盒中的黑球数没有任何影响.
①和②出现的次数是一样的,所以对B选项中的乙盒中的红球数与丙盒中的黑球数的影响次数一样.
综上,选B.
法二:若袋中有两个球,则红球、黑球各一个,若红球放在甲盒,则黑球放在乙盒,丙盒中没有球,此时乙盒中黑球多于丙盒中黑球,乙盒中黑球比丙盒中红球多,故可排除A、D;若袋中有四个球,则红球、黑球各两个,若取出两个红球,则红球一个放在甲盒,余下一个放在乙盒,再取出余下的两个黑球,一个放在甲盒,则余下一个放在丙盒,所以甲盒中一红一黑,乙盒中一个红球,丙盒中一个黑球,此时乙盒中红球比丙盒中红球多,排除C,故选B.
3.(2016·全国卷Ⅱ)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
解析:法一:由题意得丙的卡片上的数字不是2和3.
若丙的卡片上的数字是1和2,则由乙的说法知乙的卡片上的数字是2和3,则甲的卡片上的数字是1和3,满足题意;
若丙的卡片上的数字是1和3,则由乙的说法知乙的卡片上的数字是2和3,则甲的卡片上的数字是1和2,不满足甲的说法.
故甲的卡片上的数字是1和3.
法二:因为甲与乙的卡片上相同的数字不是2,所以丙的卡片上必有数字2.又丙的卡片上的数字之和不是5,所以丙的卡片上的数字是1和2.因为乙与丙的卡片上相同的数字不是1,所以乙的卡片上的数字是2和3,所以甲的卡片上的数字是1和3.
答案:1和3
4.(2014·全国卷Ⅰ)甲、乙、丙三位同学被问到是否去过A,B,C三个城市时,
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市;
丙说:我们三人去过同一个城市.
由此可判断乙去过的城市为________.
解析:由甲、丙的回答易知甲去过A城市和C城市,乙去过A城市或C城市,结合乙的回答可得乙去过A城市.
答案:A
一、选择题
1.下面几种推理是合情推理的是( )
①由圆的性质类比出球的有关性质;
②由直角三角形、等腰三角形、等边三角形的内角和是180°,归纳出所有三角形的内角和都是180°;
③教室内有一把椅子坏了,则该教室内的所有椅子都坏了;
④三角形内角和是180°,四边形内角和是360°,五边形内角和是540°,由此得出凸多边形的内角和是(n-2)·180°.
A.①②④ B.①③④
C.②③④ D.①②③④
解析:选A 根据题意,依次分析4个推理:
对于①,在推理过程中由圆的性质类比出球的有关性质,是类比推理;
对于②,符合归纳推理的定义,即是由特殊到一般的推理过程,是归纳推理;
对于③,不是合情推理,
对于④,符合归纳推理的定义,即是由特殊到一般的推理过程,是归纳推理,所以是合情推理的是①②④.
2.已知①正方形的对角线相等;②平行四边形的对角线相等;③正方形是平行四边形.由①②③组合成“三段论”,根据“三段论”推理出一个结论,则这个结论是( )
A.正方形是平行四边形 B.平行四边形的对角线相等
C.正方形的对角线相等 D.以上均不正确
解析:选C 由演绎推理三段论可得,
“平行四边形的对角线相等”为大前提,
“正方形是平行四边形”为小前提,
则结论为“正方形的对角线相等”.
3.将正奇数按如图所示的规律排列,则第21行从左向右的第5个数为( )
A.731 B.809
C.852 D.891
解析:选B 由题意知,前20行共有正奇数1+3+5+…+39=202=400个,
则第21行从左向右的第5个数是第405个正奇数,
所以这个数是2×405-1=809.
4.某校高二(1)班每周都会选出两位“迟到之星”,在“迟到之星”人选揭晓之前,小马说:“两个人选应该在小赵、小宋和小谭三人之中产生”,小赵说:“一定没有我,肯定有小宋”,小宋说:“小马、小谭二人中有且仅有一人是迟到之星”,小谭说:“小赵说的对”.已知这四人中有且只有两人的说法是正确的,则“迟到之星”是( )
A.小赵、小谭 B.小马、小宋
C.小马、小谭 D.小赵、小宋
解析:选A 小马说:“两个人选应该是在小赵、小宋和小谭三人之中产生”,
如果小马说假话,则小赵、小宋、小谭说的都是假话,不合题意,所以小马说的是真话;
小赵说:“一定没有我,肯定有小宋”是假话,
否则,小谭说的是真话,这样有三人说真话,不合题意;
小宋说:“小马、小谭二人中有且仅有一人是迟到之星”,是真话;
小谭说:“小赵说的对”,是假话;
这样,四人中有且只有小马和小宋的说法是正确的,
且“迟到之星”是小赵和小谭.
5.将正整数排列如下:
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
…
则图中数2 018出现在( )
A.第44行第83列 B.第45行第83列
C.第44行第82列 D.第45行第82列
解析:选D 由题意可知第n行有2n-1个数,则前n行的数的个数为1+3+5+…+(2n-1)=n2,因为442=1 936,452=2 025,且1 936<2 018<2 025,所以2 018在第45行,又第45行有2×45-1=89个数,2 018-1 936=82,故2 018在第45行第82列,选D.
6.单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数,则f(n)=( )
A.3n2-3n+1 B.3n2-3n+2
C.3n2-3n D.3n2-3n-1
解析:选A 由于f(2)-f(1)=7-1=6,
f(3)-f(2)=19-7=2×6,
f(4)-f(3)=37-19=3×6,
f(5)-f(4)=61-37=4×6,…
因此,当n≥2时,有f(n)-f(n-1)=6(n-1),
所以f(n)=[f(n)-f(n-1)]+[f(n-1)-f(n-2)]+…+[f(2)-f(1)]+f(1)=6[(n-1)+(n-2)+…+2+1]+1=3n2-3n+1.
又f(1)=3×12-3×1+1=1,所以f(n)=3n2-3n+1.
7.以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算法》一书中的“杨辉三角形”.
1 2 3 4 5 … 2 015 2 016 2 017 2 018
3 5 7 9 ………… 4 031 4 033 4 035
8 12 16 ……………… 8 064 8 068
20 28 …………………… 16 132
………………………………
该表由若干行数字组成,从第二行起,第一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )
A.2 019×22 015 B.2 019×22 016
C.2 018×22 017 D.2 018×22 016
解析:选B 当第一行为2个数时,最后一行仅一个数,为3=3×1=3×20;
当第一行为3个数时,最后一行仅一个数,为8=4×2=4×21;
当第一行为4个数时,最后一行仅一个数,为20=5×4=5×22;
当第一行为5个数时,最后一行仅一个数,为48=6×8=6×23;
归纳推理得,当第一行为2 018个数时,最后一行仅一个数,为2 019×22 016.
8.我国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一直角边为股,斜边为弦.若a,b,c为直角三角形的三边,其中c为斜边,则a2+b2=c2,称这个定理为勾股定理.现将这一定理推广到立体几何中:在四面体O ABC中,∠AOB=∠BOC=∠COA=90°,S为顶点O所对面的面积,S1,S2,S3分别为侧面△OAB,△OAC,△OBC的面积,则下列选项中对于S,S1,S2,S3满足的关系描述正确的为( )
A.S2=S+S+S
B.S2=++
C.S=S1+S2+S3
D.S=++
解析:选A 如图,作OD⊥ BC于点D,连接AD,由立体几何知识知,AD⊥BC,从而S2=2=BC2·AD2=BC2·(OA2+OD2)=(OB2+OC2)·OA2+BC2·OD2=2+2+2
=S+S+S.
二、填空题
9.如果函数f(x)在区间D上是凸函数,那么对于区间D内的任意x1,x2,…,xn,都有≤f.若y=sin x在区间(0,π)上是凸函数,那么在△ABC中,sin A+sin B+sin C的最大值是________.
解析:由题意知,凸函数满足
≤f,
又y=sin x在区间(0,π)上是凸函数,则sin A+sin B+sin C≤3sin=3sin=.
答案:
10.(2018·湛江一模)如图,已知点O是△ABC内任意一点,连接AO,BO,CO
,并延长交对边于A1,B1,C1则++=1,类比猜想:点O是空间四面体ABCD内任意一点,连接AO,BO,CO,DO,并延长分别交平面BCD,ACD,ABD,ABC于点A1,B1,C1,D1,则有____________.
解析:猜想:若O为四面体ABCD内任意一点,连接AO,BO,CO,DO,并延长分别交平面BCD,ACD,ABD,ABC于点A1,B1,C1,D1,则+++=1.用等体积法证明如下:+++=+++=1.
答案:+++=1
11.(2017·北京高考)某学习小组由学生和教师组成,人员构成同时满足以下三个条件:
(ⅰ)男学生人数多于女学生人数;
(ⅱ)女学生人数多于教师人数;
(ⅲ)教师人数的两倍多于男学生人数.
①若教师人数为4,则女学生人数的最大值为________.
②该小组人数的最小值为________.
解析:令男学生、女学生、教师人数分别为x,y, ,
则 <y<x<2 .
①若教师人数为4,则4<y<x<8,
当x=7时,y取得最大值6.
②当 =1时,1= <y<x<2,不满足条件;
当 =2时,2= <y<x<4,不满足条件;
当 =3时,3= <y<x<6,y=4,x=5,满足条件.
所以该小组人数的最小值为3+4+5=12.
答案:6 12
12.已知cos=,
coscos=,
coscoscos=,
……
(1)根据以上等式,可猜想出的一般结论是________;
(2)若数列{an}中,a1=cos,a2=coscos,
a3=coscoscos,…,
前n项和Sn=,则n=________.
解析:(1)从题中所给的几个等式可知,第n个等式的左边应有n个余弦相乘,且分母均为2n+1,分子分别为π,2π,…,nπ,右边应为,故可以猜想出结论为
coscos·…·cos=(n∈N*).
(2)由(1)可知an=,故Sn==1-
==,解得n=10.
答案:(1)coscos·…·cos=(n∈N*)
(2)10
三、解答题
13.在锐角三角形ABC中,求证:sin A+sin B+sin C>cos A+cos B+cos C.
证明:∵△ABC为锐角三角形,
∴A+B>,∴A>-B,
∵y=sin x在上是增函数,
∴sin A>sin=cos B,
同理可得sin B>cos C,sin C>cos A,
∴sin A+sin B+sin C>cos A+cos B+cos C.
14.某少数民族的刺绣有着悠久的历史,图中(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮,向按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求f(6)的值;
(2)求f(n)的表达式;
(3)求证:当n≥2时,+++…+<.
解:(1)f(1)=1,
f(2)=1+4=5,
f(3)=1+4+8=13,
f(4)=1+4+8+12=25,
f(5)=1+4+8+12+16=41,
f(6)=1+4+8+12+16+20=61.
(2)∵f(2)-f(1)=4=4×1,
f(3)-f(2)=8=4×2,
f(4)-f(3)=12=4×3,
f(5)-f(4)=16=4×4,
由上式规律得出f(n+1)-f(n)=4n.
∴f(n)-f(n-1)=4×(n-1),
f(n-1)-f(n-2)=4×(n-2),
f(n-2)-f(n-3)=4×(n-3),
……
f(2)-f(1)=4×1,
∴f(n)-f(1)=4[(n-1)+(n-2)+…+2+1]
=2(n-1)·n,
∴f(n)=2n2-2n+1.
(3)证明:当n≥2时,==,
∴+++…+
=1+
=1+=-.
由于g(n)=-为递增数列,
即有g(n)≥g(1)=1,且g(n)<,
故+++…+<.
1.为弘扬中国传统文化,某校在高中三个年级中抽取甲、乙、丙三名同学进行问卷调查.调查结果显示这三名同学来自不同的年级,加入了不同的三个社团:“楹联社”“书法社”“汉服社”,还满足如下条件:
(1)甲同学没有加入“楹联社”;
(2)乙同学没有加入“汉服社”;
(3)加入“楹联社”的那名同学不在高二年级;
(4)加入“汉服社”的那名同学在高一年级;
(5)乙同学不在高三年级.
则甲同学所在的社团是( )
A.楹联社 B.书法社
C.汉服社 D.条件不足无法判断
解析:选C 假设乙在高一,则由(4)知乙加入“汉服社”,与(2)矛盾,
结合(5)知,乙在高二年级.根据(3),可得乙加入“书法社”.
根据(1)可知甲同学没有加入“楹联社”,
可得甲同学所在的社团是汉服社.
2.已知13+23=32,13+23+33=62,13+23+33+43=102,…,若13+23+33+43+…+n3=3 025,则n=( )
A.8 B.9
C.10 D.11
解析:选C ∵13+23=32=(1+2)2,
13+23+33=62=(1+2+3)2,
13+23+33+43=102=(1+2+3+4)2,
……
∴13+23+33+…+n3=(1+2+3+…+n)2=.
∵13+23+33+43+…+n3=3 025,
∴=3 025,∴n2(n+1)2=(2×55)2,
∴n(n+1)=110,解得n=10.
高考研究课(四)
证明4方法 ——综合法、分析法、反证法、数学归纳法
[全国卷5年命题分析]
考点
考查频度
考查角度
直接证明与间接证明
5年6考
综合法、分析法、反证法证明问题
数学归纳法
未考查
分析法
[典例] 已知非零向量a,b,且a⊥b,求证:≤.
[证明] a⊥b⇔a·b=0,要证≤.
只需证|a|+|b|≤ |a+b|,
只需证|a|2+2|a||b|+|b|2≤2(a2+2a·b+b2),
只需证|a|2+2|a||b|+|b|2≤2a2+2b2,
只需证|a|2+|b|2-2|a||b|≥0,即(|a|-|b|)2≥0,
上式显然成立,故原不等式得证.
[方法技巧]
分析法证明问题的思路与适用范围
(1)分析法的思路:
“执果索因”,逐步寻找结论成立的充分条件,即从“未知”看“需知”,逐步靠拢“已知”或本身已经成立的定理、性质或已经证明成立的结论等,通常采用“要证—只需证—已知”的格式,在表达中要注意叙述形式的规范性.
(2)分析法证明问题的适用范围:
当已知条件与结论之间的联系不够明显、直接,或证明过程中所需用的知识不太明确、具体时,往往采用分析法,特别是含有根号、绝对值的等式或不等式,常考虑用分析法.
[即时演练]
已知△ABC的三个内角A,B,C成等差数列,A,B,C的对边分别为a,b,c.
求证:+=.
证明:要证+=,
即证+=3也就是+=1,
只需证c(b+c)+a(a+b)=(a+b)(b+c),
需证c2+a2=ac+b2,
又△ABC的三内角A,B,C成等差数列,故B=60°,
由余弦定理,得b2=c2+a2-2accos 60°,
即b2=c2+a2-ac,故c2+a2=ac+b2成立.
于是原等式成立.
综合法
综合法证明问题是历年高考的热点问题,也是必考问题之一.通常在解答题中出现.
常见的命题角度有:
(1)立体几何证明题;
(2)数列证明题;
(3)与函数、方程、不等式结合的证明题.
角度一:立体几何证明题
1.如图,在三棱锥P ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.
求证:(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
证明:(1)因为D,E分别为棱PC,AC的中点,所以DE∥PA.
又因为PA⊄平面DEF,DE⊂平面DEF,
所以直线PA∥平面DEF.
(2)因为D,E,F分别为棱PC,AC,AB的中点,PA=6,BC=8,
所以DE∥PA,EF∥BC,DE=PA=3,EF=BC=4.
又因为DF=5,故DF2=DE2+EF2,
所以∠DEF=90°,即DE⊥EF.
又PA⊥AC,DE∥PA,所以DE⊥AC.
因为AC∩EF=E,AC⊂平面ABC,EF⊂平面ABC,
所以DE⊥平面ABC.
又DE⊂平面BDE,所以平面BDE⊥平面ABC.
角度二:数列证明题
2.已知函数f(x)满足f(x+y)=f(x)·f(y)且f(1)=.
(1)当n∈N*时,求f(n)的表达式;
(2)设an=n·f(n),n∈N*,求证:a1+a2+a3+…+an<2.解:(1)因为函数f(x)满足f(x+y)=f(x)·f(y),
所以令y=1,得f(x+1)=f(x)·f(1),
所以f(n+1)=f(n)·f(1).
又因为f(1)=,所以=,
所以f(n)=n(n∈N*).
(2)证明:由(1)得an=n·n,
设Tn=a1+a2+a3+…+an-1+an,则
Tn=1×+2×2+3×3+…+(n-1)×n-1+n×n,①
所以Tn=1×2+2×3+…+(n-2)n-1+(n-1)×n+n×n+1,②
所以由①-②得
Tn=+2+3+…+n-1+n-n·n+1=-n·n+1=1-n-n·n+1=1-,
所以Tn=2-<2,
即a1+a2+a3+…+an-1+an<2.
角度三:与函数、方程、不等式结合的证明题
3.已知定义在R上的函数f(x)=ax3+bx2+cx(a0.
∵f(x)的图象上有一点处的切线的斜率为-a,
∴方程ax2+bx+c+a=0有实数根,
∴Δ=b2-4a(a+c)≥0,即b2-4a(-b)≥0,
整理得2+4·≥0,解得≥0或≤-4.
由a+b+c=0,b-.
由a0,∴b2-4ac>0,
故方程f′(x)=0必有两个不相等的实数根,
设为x1,x2,且x1-2.
若f′(x)在区间(s,t)上恒非负,则有x1≤s0),数列{an}满足a1=(a>0),an+1=f(an)(n∈N*)
(1)求a2,a3,a4,并猜想数列{an}的通项公式;
(2)用数学归纳法证明(1)中的猜想.
解:(1)∵f(x)=(x>0),数列{an}满足a1=(a>0),an+1=f(an)(n∈N*),
∴an+1=,∴a2=,a3=,a4=.
猜想an=.
(2)利用数学归纳法证明:an=.
①当n=1时,由(1)可知成立.
②假设n= ( ≥1, ∈N*)时成立,即a =.
则n= +1时,
a +1==,
因此n= +1时也成立,
综上可得,an=对于n∈N*都成立.
[方法技巧]
(1)利用数学归纳法可以探索与正整数n有关的未知问题、存在性问题,其基本模式是“归纳—猜想—证明”,即先由合情推理发现结论,然后经逻辑推理即演绎推理论证结论的正确性.
(2)“归纳—猜想—证明”的基本步骤是“试验—归纳—猜想—证明”.高中阶段该部分与数列结合的问题是最常见的问题.
1.(2014·山东高考)用反证法证明命题“设a,b为实数,则方程x3+ax+b=0至少有一个实根”时,要做的假设是( )
A.方程x3+ax+b=0没有实根
B.方程x3+ax+b=0至多有一个实根
C.方程x3+ax+b=0至多有两个实根
D.方程x3+ax+b=0恰好有两个实根
解析:选A 至少有一个实根的否定是没有实根,故要做的假设是“方程x3+ax+b=0没有实根”.
2.(2017·全国卷Ⅱ)已知函数f(x)=ax2-ax-xln x,且f(x)≥0.
(1)求a;
(2)证明:f(x)存在唯一的极大值点x0,且e-21时,g′(x)>0,g(x)单调递增.
所以x=1是g(x)的极小值点,故g(x)≥g(1)=0.
综上,a=1.
(2)证明:由(1)知f(x)=x2-x-xln x(x>0),
f′(x)=2x-2-ln x.
设h(x)=2x-2-ln x,则h′(x)=2-.
当x∈时,h′(x)<0;
当x∈时,h′(x)>0.
所以h(x)在上单调递减,在上单调递增.
又h(e-2)>0,h<0,h(1)=0,所以h(x)在上有唯一零点x0,在上有唯一零点1,且当x∈(0,x0)时,h(x)>0;当x∈(x0,1)时,h(x)<0;
当x∈(1,+∞)时,h(x)>0.
因为f′(x)=h(x),
所以x=x0是f(x)的唯一极大值点.
由f′(x0)=0得ln x0=2(x0-1),
故f(x0)=x0(1-x0).
由x0∈,得f(x0)<.
因为x=x0是f(x)在(0,1)的最大值点,
由e-1∈(0,1),f′(e-1)≠0,得f(x0)>f(e-1)=e-2.
所以e-20,证明:d1,d2,…,dn-1是等比数列;
解:(1)d1=2,d2=3,d3=6.
(2)证明:因为a1>0,公比q>1,
所以a1,a2,…,an是递增数列.
因此,对i=1,2,…,n-1,Ai=ai,Bi=ai+1.
于是对i=1,2,…,n-1,
di=Ai-Bi=ai-ai+1=a1(1-q)qi-1.
因此di≠0且=q(i=1,2,…,n-2),
即d1,d2,…,dn-1是等比数列.
4.(2014·安徽高考)设实数c>0,整数p>1,n∈N*.
(1)证明:当x>-1且x≠0时,(1+x)p>1+px;
(2)数列{an}满足a1>c,an+1=an+a.
证明:an>an+1>c.
证明:(1)用数学归纳法证明:
①当p=2时,(1+x)2=1+2x+x2>1+2x,原不等式成立.
②假设p= ( ≥2, ∈N*)时,不等式(1+x) >1+ x成立.
当p= +1时,(1+x) +1=(1+x)(1+x) >(1+x)·(1+ x)=1+( +1)x+ x2>1+( +1)x.
所以p= +1时,原不等式也成立.
综合①②可得,当x>-1,x≠0时,对一切整数p>1,不等式(1+x)p>1+px均成立.
(2)先用数学归纳法证明an>c.
①当n=1时,由题设知a1>c成立.
②假设n= ( ≥1, ∈N*)时,不等式a >c成立.
由an+1=an+a易知an>0,n∈N*.
当n= +1时,=+a=1+.
由a >c>0得-1<-<<0.
由(1)中的结论得p=p>1+p·=.
因此a>c,即a +1>c.
所以n= +1时,不等式an>c也成立.
综合①②可得,对一切正整数n,不等式an>c均成立.
再由=1+可得<1,即an+1an+1>c,n∈N*.
一、选择题
1.设x=,y=-, =-,则x,y, 的大小关系是( )
A.x>y> B. >x>y
C.y> >x D.x> >y
解析:选D 由题意知x,y, 都是正数,又x2- 2=2-(8-4)=4-6=->0,∴x> .
∵==>1,∴ >y,∴x> >y.
2.对于定义域为D的函数y=f(x)和常数c,若对任意正实数ξ,∃x0∈D,使得0<|f(x0)-c|<ξ恒成立,则称函数y=f(x)为“敛c函数”.现给出如下函数:
①f(x)=x(x∈ );②f(x)=x+1(x∈ );
③f(x)=log2x;④f(x)=.
其中为“敛1函数”的有( )
A.①② B.③④
C.②③④ D.①②③
解析:选C 由题意知,函数f(x)为“敛1函数”等价于存在x0属于f(x)的定义域,使得f(x0)无限接近于1.对于①,f(x)=x(x∈ ),当x=1时,f(x)=1,当x≠1时,|f(x)-1|≥1,故①中函数不是“敛1函数”;对于②③④中函数,作出函数图象,结合“敛1函数”的定义易知它们都是“敛1函数”.故选C.
3.(2018·大连一模)设f(x)是定义在R上的奇函数,且当x≥0时,f(x)单调递减,若x1+x2>0,则f(x1)+f(x2)的值( )
A.恒为负值 B.恒等于零
C.恒为正值 D.无法确定正负
解析:选A 由f(x)是定义在R上的奇函数,且当x≥0时,f(x)单调递减,可知f(x)是R上的单调递减函数,
由x1+x2>0,可知x1>-x2,f(x1)-
B.-<-
C.-=-
D.不能确定
解析:选B 由题意知,(-)-(-)=(+)- (+),
因为(+)2-(+)2
=2[-]
=2(-)<0,
所以-<-.
6.已知a,b,c∈(0,+∞),则a+,b+,c+三个数( )
A.都大于6 B.至少有一个不大于6
C.都小于6 D.至少有一个不小于6
解析:选D 设a+,b+,c+都小于6,
则a++b++c+<18,
利用基本不等式,可得a++b++c+≥2 +2 +2 =8+4+6=18,
这与假设所得结论矛盾,故假设不成立,
所以a+,b+,c+三个数至少有一个不小于6.
二、填空题
7.(2018·太原模拟)用反证法证明“若x2-1=0,则x=-1或x=1”时,应假设____________________.
解析:“x=-1或x=1”的否定是“x≠-1且x≠1”.
答案:x≠-1且x≠1
8.若二次函数f(x)=4x2-2(p-2)x-2p2-p+1,在区间[-1,1]内至少存在一点c,使f(c)>0,则实数p的取值范围是________.
解析:法一:(补集法)
令解得p≤-3或p≥,
故满足条件的p的范围为.
法二:(直接法)
依题意有f(-1)>0或f(1)>0,
即2p2-p-1<0或2p2+3p-9<0,
得-0,即x1y1+x1y2+x1y3+x1y4+ x2y1+x2y2+x2y3+x2y4+x3y1+x3y2+x3y3+x3y4+x4y1+x4y2+x4y3+x4y4>0,即T1+T2+T3+T4>0,即T1,T2,T3,T4中至少有一个为正数.选A.
2.设fn(x)是等比数列1,x,x2,…,xn的各项和,其中x>0,n∈N,n≥2.
(1)证明:函数Fn(x)=fn(x)-2在内有且仅有一个零点(记为xn),且xn=+x;
(2)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为gn(x),比较fn(x)和 gn(x)的大小,并加以证明.
解:(1)证明:Fn(x)=fn(x)-2=1+x+x2+…+xn-2,
则Fn(1)=n-1>0,
Fn=1++2+…+n-2
=-2=-<0,
所以Fn(x)在内至少存在一个零点.
又F′n(x)=1+2x+…+nxn-1>0,
故Fn(x)在内单调递增,所以Fn(x)在内有且仅有一个零点xn.
因为xn是Fn(x)的零点,所以Fn(xn)=0,
即-2=0,故xn=+x.
(2)由题设,fn(x)=1+x+x2+…+xn,
gn(x)=,x>0.
当x=1时,fn(x)=gn(x).
当x≠1时,用数学归纳法可以证明fn(x)<gn(x).
①当n=2时,f2(x)-g2(x)=-(1-x)2<0,
所以f2(x)<g2(x)成立.
②假设n= ( ≥2, ∈N*)时,不等式成立,
即f (x)<g (x).
那么,当n= +1时,
f +1(x)=f (x)+x +1<g (x)+x +1=+x +1=.
又g +1(x)-
=,
令h (x)= x +1-( +1)x +1(x>0),
则h′ (x)= ( +1)x - ( +1)x -1
= ( +1)x -1·(x-1).
所以当0<x<1时,h′ (x)<0,h (x)在(0,1)上递减;
当x>1时,h′ (x)>0,h (x)在(1,+∞)上递增.
所以h (x)>h (1)=0,
从而g +1(x)>.
故f +1(x)<g +1(x),即n= +1时不等式也成立.
由①和②知,对一切n≥2的整数,都有fn(x)<gn(x).
阶段滚动检测(五)检测范围:第一单元至第十九单元(对应配套卷P357)
(时间120分钟 满分150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在复平面内,设 =a+2i(i是虚数单位),若复数 2对应的点位于虚轴的正半轴上,则实数a的值为( )
A.0 B.2
C.-2 D.2或-2
解析:选B 因为 =a+2i,
所以 2=a2-4+4ai.
因为复数 2对应的点位于虚轴的正半轴上,
所以所以a=2.
2.设U=R,集合M={x|x2+x-2>0},N=x2x-1≤,则(∁UM)∩N=( )
A.[-2,0] B.[-2,1]
C.[0,1] D.[0,2]
解析:选A 由题意可得∁UM=[-2,1],N=(-∞,0],故(∁UM)∩N=[-2,0].
3.已知函数f(x)=-x2+2,g(x)=log2|x|,则函数F(x)=f(x)·g(x)的图象大致为( )
解析:选B f(x),g(x)均为偶函数,则F(x)也为偶函数,由此排除A,D.当x>2时,-x2+2<0,log2|x|>0,所以F(x)<0,排除C,故选B.
4.某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(百分制)如下表所示:
序号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
数学
95
75
80
94
92
65
67
84
98
71
67
93
64
78
77
90
57
83
72
83
成绩
物理
成绩
90
63
72
87
91
71
58
82
93
81
77
82
48
85
69
91
61
84
78
86
若数学成绩90分(含90分)以上为优秀,物理成绩85(含85分)以上为优秀.参照公式,得到的正确结论是( )
附: 2=,
其中n=a+b+c+d.
P( 2≥ 0)
0.10
0.05
0.025
0.010
0.005
0.001
0
2.706
3.841
5.024
6.635
7.879
10.828
A.有99.5 以上的把握认为“学生的数学成绩与物理成绩有关”
B.没有99.5 以上的把握认为“学生的数学成绩与物理成绩有关”
C.在犯错误的概率不超过0.1 的前提下,认为“学生的数学成绩与物理成绩无关”
D.在犯错误的概率不超过0.1 的前提下,认为“学生的数学成绩与物理成绩有关”
解析:选A 根据题意可得2×2列联表:
物理优秀
物理不优秀
总计
数学优秀
5
1
6
数学不优秀
2
12
14
总计
7
13
20
则 2=≈8.802>7.879,因此有99.5 把握认为学生的数学成绩与物理成绩之间有关系.
5.已知数列{an}的首项为1,前n项和为Sn,若数列{an}与{Sn+2}都是公比为q的等比数列,则q的值为( )
A. B.1
C. D.2
解析:选C 根据题意可得:=q,即=q,解得q=.
6.某校组织由5名学生参加的演讲比赛,采用抽签法决定演讲顺序,在“学生A和B都不是第一个出场,B不是最后一个出场”的前提下,学生C第一个出场的概率为( )
A. B.
C. D.
解析:选A 法一:当学生A最后一个出场时,有AA=18种不同的安排方法;当学生A不是最后一个出场时,有AA=36种不同的安排方法,所以满足“A和B都不是第一个出场,B不是最后一个出场”的所有不同安排方法有18+36=54种.其中“C第一个出场”的结果有AA=18种,则所求概率为=.
法二:“A和B都不是第一个出场,B不是最后一个出场”的安排方法中,另外3人中任何一个人第一个出场的概率都相等,故“C第一个出场”的概率是.
7.执行如图所示的程序框图,若输出s的值为10,则判断框中填入的条件可以是( )
A.i<10? B.i≤10?
C.i≤11? D.i≤12?
解析:选C 由程序框图知,其运行的功能是循环计算并输出s的值,由于s=0+dx+dx+…+dx=ln xe3e2+ln xe4e3+…+ln xei+1ei=i-1=10,解得i=11,所以当i>11时,不满足判断框内的条件,退出循环,故判断框内应填i≤11?.
8.观察下列各式:55=3 125,56=15 625,57=78 125,58=390 625,59=1 953 125,…,则52 018的末四位数字为( )
A.3 125 B.5 625
C.0 625 D.8 125
解析:选B 由题意可知,n>4时,5n的末四位数字以T=4为周期,又因为2 018=4×503+6,所以52 018的末四位数字与56的末四位数字相同,即为5 625.
9.(x+2y)7展开式中系数最大的项为( )
A.68y7 B.112x3y4
C.672x2y5 D.1 344x2y5
解析:选C (x+2y)7展开式的通项为Tr+1=2rCx7-ryr,
设第r+1项系数最大,
则解得r=5,所以(x+2y)7展开式中系数最大的项为T6=25Cx2y5=672x2y5.
10.如图, 格纸上的小正方形的边长为1, 粗实线画出的是某几何体的三视图, 则该几何体的体积为( )
A.4+6π B.8+6π
C.4+12π D.8+12π
解析:选B 由三视图可知,该几何体是组合体,下面是一个底面半径为2,高为3的圆柱的一半,上面是一个高为2,底面是一个边长为3,4的矩形的四棱锥,所以该几何体的体积V=×π×22×3+×4×3×2=8+6π.
11.已知双曲线-=1(a>0,b>0)的左、右两个焦点分别为F1,F2,以线段F1F2为直径的圆与双曲线的渐近线在第一象限的交点为M,若|MF1|-|MF2|=2b,该双曲线的离心率为e,则e2=( )
A.2 B.
C. D.
解析:选D 由题意,圆的方程为x2+y2=c2,联立得即点M(a,b),
则|MF1|-|MF2|=-=2b,
即-=2,
-=2,
化简得,e4-e2-1=0,解得e2=.
12.已知函数f(x)=(e为自然对数的底数),函数g(x)满足g′(x)=f′(x)+2f(x),其中f′(x),g′(x)分别为函数f(x)和g(x)的导函数,若函数g(x)在[-1,1]上是单调函数,则实数a的取值范围为( )
A.(-∞,1] B.
C.(1,+∞) D.
解析:选B 因为f′(x)=,
所以g′(x)=f′(x)+2f(x)=.
因为函数g(x)在[-1,1]上是单调函数,
所以g′(x)≥0或g′(x)≤0.
当a=0时,g′(x)>0,满足题意;
因为ex>0,所以当a<0时, 只需ax2+2ax+1≥0在[-1,1]上成立即可,所以a+2a+1≥0,则-≤a<0;
当a>0时,只需ax2+2ax+1≥0在[-1,1]上成立,所以a-2a+1≥0,则0320)=0.5-P(300-20<ξ<300+20)=2.275 ,则用电量在320度以上的户数约为1 000P(ξ>320)≈23.
答案:23
14.已知几何体O ABCD的底面ABCD是边长为的正方形,且该几何体体积的最大值为,则该几何体外接球的表面积为________.
解析:因为该几何体体积的最大值为,所以点O到平面ABCD的距离h=,根据球的性质可得R2=2+2,所以R=,因此该几何体外接球的表面积S=4πR2=8π.
答案:8π
15.在2018年1月15日那天,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x元和销售量y件之间的一组数据如下表所示:
价格x
9
9.5
m
10.5
11
销售量y
11
n
8
6
5
由散点图可知,销售量y与价格x之间有较强的线性相关关系,其线性回归方程是
=-3.2x+40,且m+n=20,则其中的n=________.
解析:==8+,==6+,回归直线一定经过样本点中心(,),即6+=-3.2+40,即3.2m+n=42.
又因为m+n=20,即解得故n=10.
答案:10
16.设x,y满足约束条件若目标函数 =2x-y+2a+b(a>0,b>0)的最大值为3,则+的最小值为________.
解析:
作出不等式组所表示的平面区域如图中阴影部分所示,根据目标函数 与直线在y轴上的截距的关系可知,当目标函数 =2x-y+2a+b(a>0,b>0)过点A(1,0)时取得最大值3,即2a+b=1,则+=(2a+b)=3++≥3+2 =3+2,当且仅当=,即b=2a=2-时,+取得最小值3+2.
答案:3+2
三、解答题(本大题共6小题,共70分,解答时写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)在△ABC中,a,b,c分别为内角A,B,C的对边,2bsin B=(2a+c)sin A+(2c+a)sin C.
(1)求B的大小;
(2)若b=,A=,求△ABC的面积.
解:(1)∵2bsin B=(2a+c)sin A+(2c+a)sin C,
由正弦定理得,2b2=(2a+c)a+(2c+a)c,
化简得,a2+c2-b2+ac=0.
∴cos B===-.
∵00时,由f′(x)>0,得xln a,
∴f(x)的单调递增区间为(-∞,ln a),单调递减区间为(ln a,+∞).
(2)由(1)知,当a≤0时,f(x)在(-∞,+∞)上单调递减,而f(0)=0,
∴f(x)≤0在R上不可能恒成立;
当a>0时,f(x)在(-∞,ln a)上单调递增,在(ln a,+∞)上单调递减,
f(x)max=f(ln a)=aln a-a+1.
令g(a)=aln a-a+1,
依题意有g(a)≤0,而g′(a)=ln a,且a>0,
∴g(a)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴g(a)min=g(1)=0,故a=1.
(3)证明:由(2)知:a=1时,f(ln x)=ln x-x+1≤0恒成立,所以有ln x≤x-1(x>0).
则==-1<-1=-1,
又由ln x≤x-1知-ln x≥1-x在(0,+∞)上恒成立,
∴=-1=-1>-1=-1.
综上所述:对任意的0