- 822.50 KB
- 2021-04-20 发布
2016~2017学年度高三年级第一学期期末联考
数学试题(文科)
考试时间:120分钟 满分:150分
第Ⅰ卷
一、选择题:本题共12小题,每小题5分, 在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则集合中元素的个数为( )
A.5
B.4
C.3
D.2
2. 设复数满足,则的共轭复数为( )
A.
B.
C.
D.
3. 设,记,则的大小关系为
A.
C.
B.
D.
4. 执行如图所示的程序框图,若输入的、分别
为、,则输出的( )
A. B.
C. D.
5.《九章算术》是我国古代的数学名著,书中有如下问题:“今有
五人分五钱,令上二人所得与下三人等。问各得几何.”其意思
为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、
丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.
问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为( )
A. 钱
B. 钱
C. 钱
D. 钱
6. 已知的图象与的图象的相邻两交点间的距离为π,要得到的图象,只需把的图象( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
7. 某一简单几何体的三视图如图,则该几何体的表面积为
( )
A.
B.
C.
D.
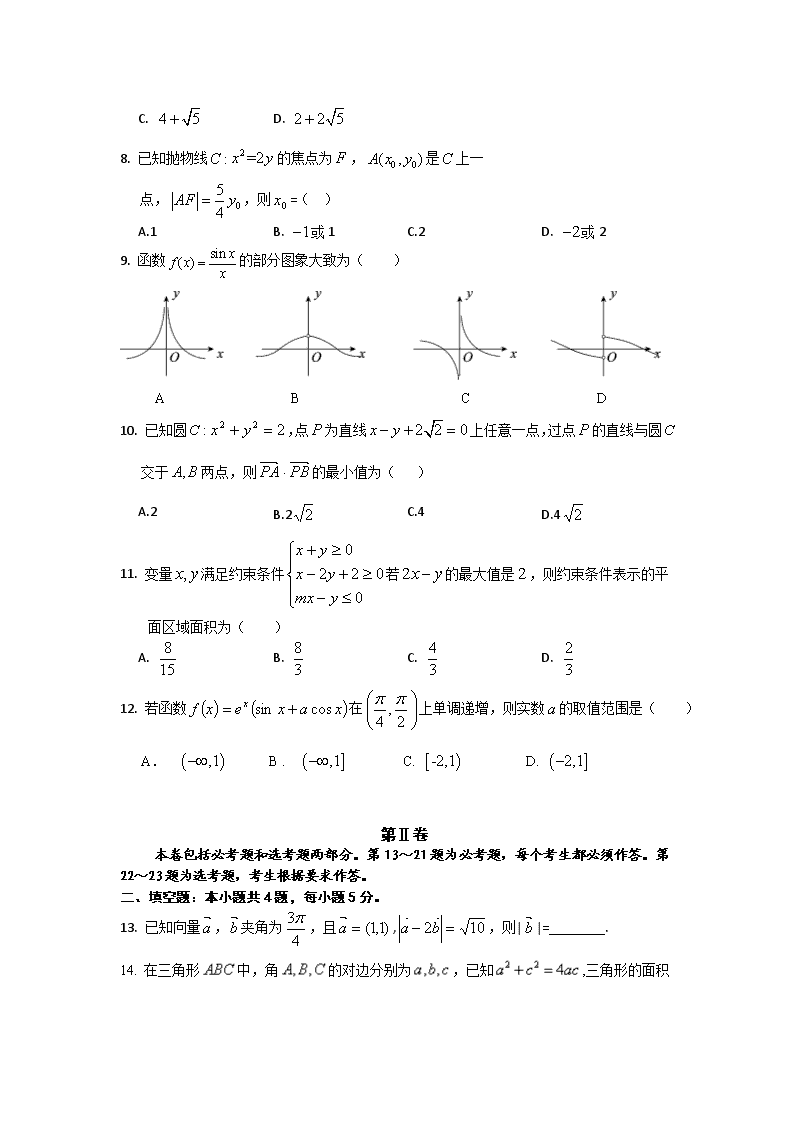
8. 已知抛物线的焦点为,是上一
点,,则=( )
A.1
B. 或1
C.2
D. 或2
9. 函数的部分图象大致为( )
A B C D
10. 已知圆,点为直线上任意一点,过点的直线与圆交于两点,则·的最小值为( )
A.2
B.2
C.4
D.4
11. 变量满足约束条件若的最大值是,则约束条件表示的平面区域面积为( )
A.
B.
C.
D.
12. 若函数在上单调递增,则实数的取值范围是( )
A. B . C. D.
第Ⅱ卷
本卷包括必考题和选考题两部分。第13~21题为必考题,每个考生都必须作答。第22~23题为选考题,考生根据要求作答。
二、填空题:本小题共4题,每小题5分。
13. 已知向量,夹角为,且,,则||=________.
14. 在三角形中,角的对边分别为,已知
,三角形的面积为,则的值为______.
15. 已知函数,则使得成立的的取值范围是______.
16. 已知四棱锥中,平面平面,其中四边形为正方形,为等边三角形,,则四棱锥外接球的体积为______.
三、解答题:解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分12分)
已知数列满足: 且,.
(1)求数列{}的通项公式;
(2)若,求数列{}的前n项和.
18. (本小题满分12分)
设函数
(1)求函数的最小正周期和单调递增区间;
(2)若且,求.
19. (本小题满分12分)
如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C 为菱形,B1C与BC1交于点O,AO⊥平面BB1C1C
(1)求证:平面ABC1⊥平面A1B1C;
(2)若AC⊥AB1,∠BCC1=120°,BC=1,
求点B1到平面ABC的距离.
20. (本小题满分12分)
已知椭圆E:的右焦点,长轴的左、右端点分别为;且.
(1)求椭圆的方程;
(2)已知点,经过点且斜率为的直线与椭圆交于不同的两点(均异于点),证明:直线与的斜率之和为定值.
21. (本小题满分12分)
已知函数,其中为常数
(1)当时,若在区间上的最大值为,求的值;
(2)当时,若存在零点,求实数的取值范围.
请考生在第22~23题中任选一题作答,如果多做,则按所做的第一题计分。
22.(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线的极坐标方程是,以极点为原点,极轴为轴的正半轴,建立平面直角坐标系,直线过点,倾斜角为.
(1)求曲线的直角坐标方程与直线的参数方程;
(2)设直线与曲线交于两点,求的值.
23.(本小题满分10分)选修4-5:
不等式选讲已知函数
(1)当时,求不等式的解集;
(2)设函数,当时,求的取值范围.
2016~2017学年度高三年级第一学期期末联考
数学试题(文科)参考答案及评分标准
一、选择题(每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
D
A
B
B
D
D
B
A
C
B
二、填空题(每小题4分,共20分)
13. 1 14. 15. 16.
三、解答题(共70分)
17. (本题满分12分)
(1)数列满足: 故数列为等比数列
设,可化为,得,,,所以…………(4分)
(2)
①
② …………(6分)
由①-②得
即
故…………(12分)
18.(本题满分12分)解:
(1)……………(3分)
的最小正周期为 ……………(4分)
由
得
的单调递增区间为 ……………(6分)
(2)
……………(8分)
由知
……………(10分)
……………(12分)
19.(本题满分12分)
(1)证明:因为为交的交点,又因为侧面为菱形,所以
……………(2分)
又平面,所以
即,故平面且
由于平面,故平面平面 ……………(5分)
(2)作,垂足为,连接
作,垂足为,由于,
故平面,所以 ……………(7分)
又,所以平面
因为,所以为等边三角形
又,可得
由于且
又为的中点,所以点到平面的距离为 ……………(12分)
20.(本题满分12分)
(1)设,则,
由,得,所以
所以椭圆E的方程为
(2)证明:由题设知,直线的方程为
代入得
由已知 设,,
则,
从而点线BP,BQ的斜率之和 ……………(6分)
故直线与的斜率之和为定值 ……………(12分)
21.(本题满分12分)
-3,
a=-e ………5分
………12分
………8分
22.(本题满分10分)解:
(1)曲线C的直角坐标方程为 ……………(2分)
直线的参数方程为(t为参数)
即(t为参数) ……………(5分)
(2)设A、B对应的参数分别为t1,t2
把直线的参数方程代入曲线方程得
整理得
……………(10分)
23.(本题满分10分)解:
(1)当时,
解不等式得
因此不等式的解集为 ……………(5分)
(2)当时,
当时等号成立,所以当时
等价于
当时,
当时,无解,所以 ……………(10分)