- 713.50 KB
- 2021-04-20 发布
临川实验学校2017—2018学年度上学期
高二年级第一次考试数学试卷
分值:150分 考试时间:120分钟
说明:1.该卷由卷Ⅰ、Ⅱ两部分组成;
2.答案填在试卷答题卡内方有效。
卷Ⅰ
一、单项选择题(本大题共12小题,每题5分,共60分)
1.已知集合,,则( )
A. B. C. D.
2.已知变量与正相关,且由观测数据算得样本平均数,,则由该观测的数据算得的线性回归方程可能是( )
A. B. C. D.
3.已知m,n表示两条不同的直线,表示平面。下列说法正确的是( )
A.若m∥,n∥,则m∥n B.若m⊥,n,则m⊥n
C.若m⊥,n⊥m,则∥n D.若m∥,n⊥m,则n⊥
4. 若,则的取值范围是
A.0,2] B.-2,0] C.-2,] D.(,-2]
5.点()在直线上,则直线的倾斜角为( )
A. 30° B. 45° C. 60° D. 120°
6.从编号为0,1,2,…,79的80件产品中,采用系统抽样的方法抽取容量为5的一个样本,若编号为42的产品在样本中,则该样本中产品的最小编号为( )
A. 2 B. 10 C.12 D.22
7.设,,,则( )
A. B. C. D.
8.设函数,则不等式的解集是( )
开始
?
是
输入p
结束
输出
否
A. B.
C. D.
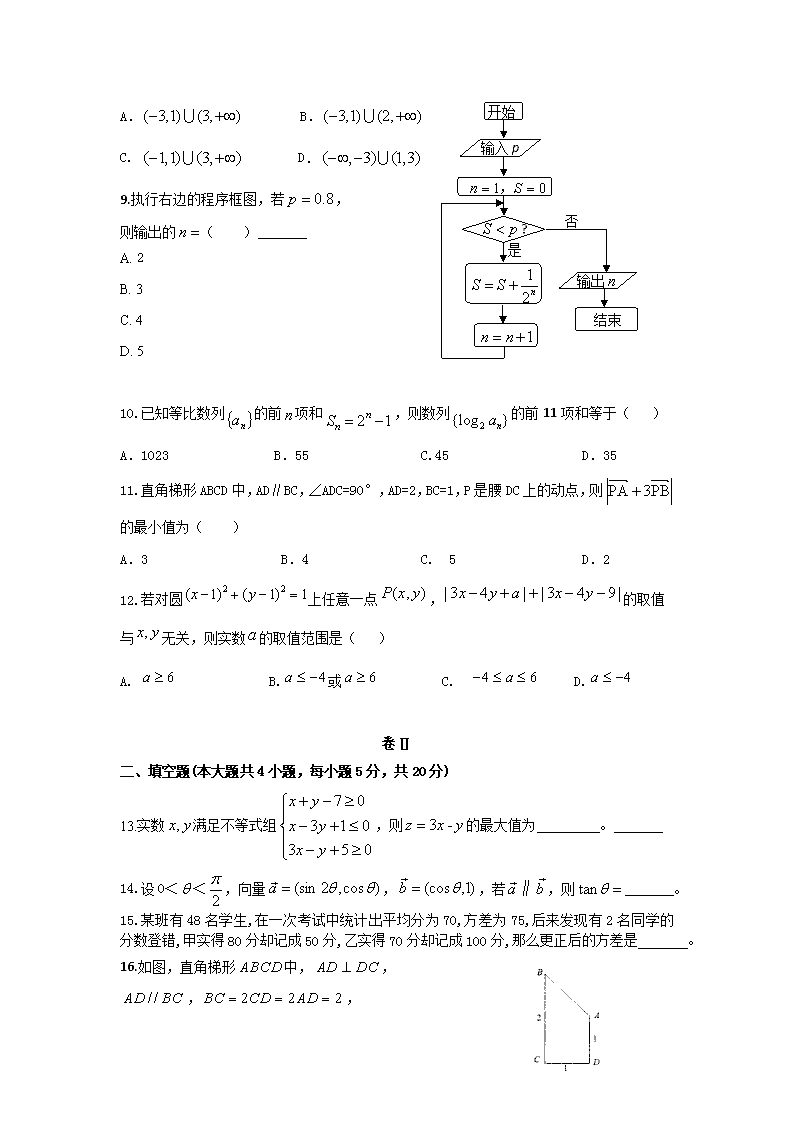
9. 执行右边的程序框图,若,
则输出的( )
A. 2
B. 3
C. 4
D. 5
10.已知等比数列的前项和,则数列的前11项和等于( )
A.1023 B.55 C.45 D.35
11. 直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=1,P是腰DC上的动点,则的最小值为( )
A.3 B.4 C. 5 D.2
12. 若对圆上任意一点,的取值与无关,则实数的取值范围是( )
A. B.或 C. D.
卷Ⅱ
二、 填空题(本大题共4小题,每小题5分,共20分)
13.实数满足不等式组,则的最大值为 。
14.设0<<,向量,,若,则 。
15.某班有48名学生,在一次考试中统计出平均分为70,方差为75,后来发现有2名同学的分数登错,甲实得80分却记成50分,乙实得70分却记成100分,那么更正后的方差是 。
16.如图,直角梯形中,,
,,
若将直角梯形绕边旋转一周,
则所得几何体的表面积为 。
三、解答题(本大题共6题,共70分,解答应写出文字说明)
17. (10分)某校从参加高三模拟考试的学生中随机抽取
60名学生,按其数学成绩(均为整数)分成六组
,,…,后得到如下部分
频率分布直方图,观察图中的信息,回答下列问题:
(1)补全频率分布直方图;
(2)估计本次考试的数学平均成绩(同一组中的数据用该组区间的中点值作代表)。
18.(12分)已知等差数列的前项和为,且,。
(1)求数列的通项公式;
(2)令,求数列的前项和。
19.(12分)已知以点为圆心的圆与直线相切,过点的动直线与圆相交于两点。
(1)求圆的方程;(2)当时,求直线的方程。
20.(12分) 如图,已知三棱锥中,为的中点,为的中点,且为正三角形.
(1)求证:平面;
(2)求证:平面平面。
21.(12分)设函数,其中,已知。
(1)求;
(2)将函数的图像上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图像向左平移个单位,得到函数的图像,求在上的最小值。
22. (12分)
已知二次函数的最小值为-1,且对任意的都有。
(1) 求函数的解析式;
(2) 设,若在-1,1]上是减函数,求实数的取值范围;
(3) 设函数,若此函数的定义域为非空数集,且不存在零点,求实数的取值范围。
高二年级第一次考试数学试卷答案
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
C
B
B
D
C
B
B
A
C
B
C
A
12、【解析】要使符合题意,则圆上所有点在直线之间,
因为圆心到直线的距离且,则所有圆心到直线的距离,且,解得。
二、填空题
13、13 14、 15、50 16、
三、解答题
17. 解:(1)分数在120,130)内的频率,
因此补充的长方形的高为0.03
(2)估计平均分为
18.(Ⅰ)设等差数列的公差为,由可得,
即,所以,解得.
.
(Ⅱ)由(Ⅰ)可得:.
.
19. 试题解析:(1)由题意知到直线的距离为圆半径
圆的方程为
(2)设线段的中点为,连结,则由垂径定理可知,且,在中由勾股定理易知
当动直线的斜率不存在时,直线的方程为时,显然满足题意;
当动直线的斜率存在时,设动直线的方程为:
由到动直线的距离为1得
或为所求方程.
20.解:
21. (Ⅰ)因为,
所以
由题设知,
所以,.
故,,又,
所以.
(2)由(1)得:
所以
因为,
所以,
当,即时,取得最小值.
22.