- 241.50 KB
- 2021-04-20 发布
淄博一中2017—2018学年度第一学期期中模块考试
高二数学理试题
命题人:闫炳杰 审核人:钱汝富
(第一卷)
一、 选择题(本大题共12小题,共60分,只有一个选项正确)
1.已知x,y∈R,且x>y>0,则( )
A. ->0
B. sinx-siny>0
C. ()x-()y<0
D. lnx+lny>0
2.若不等式x2-ax+b<0的解集为(1,2),则不等式<的解集为( )
A. (,+∞)
B. (-∞,0)∪(,+∞)
C. (,+∞)
D. (-∞,0)∪(,+∞)
3.“-3<a<1”是“存在x∈R,使得|x-a|+|x+1|<2”的( )
A. 充分非必要条件
B. 必要非充分条件
C. 充要条件
D. 既非充分又非必要条件
4.命题“∀x∈(0,1),x2-x<0”的否定是( )
A. ∃x0∉(0,1),
B. ∃x0∈(0,1),
C. ∀x0∉(0,1),
D. ∀x0∈(0,1),
5.已知x,y为正实数,则的最小值为( )
A.
B.
C.
D. 3
6.已知椭圆+=1(m>0)的焦距为8,则m的值为( )
A. 3或
B. 3
C.
D. ±3或
7.一个总体中有600个个体,随机编号为001,002,…,600,利用系统抽样方法抽取容量为24的一个样本,总体分组后在第一组随机抽得的编号为006,则在编号为051~125之间抽得的编号为( )
A. 056,080,104
B. 054,078,102
C. 054,079,104
D. 056,081,106
8.已知x,y是[0,1]上的两个随机数,则x,y满足y>2x的概率为( )
A.
B.
C.
D.
9. P是椭圆+=1上一点,F1、F2分别是椭圆的左、右焦点,若∠F1PF2=,则△F1PF2的面积为( )
A.
B.
C.
D.
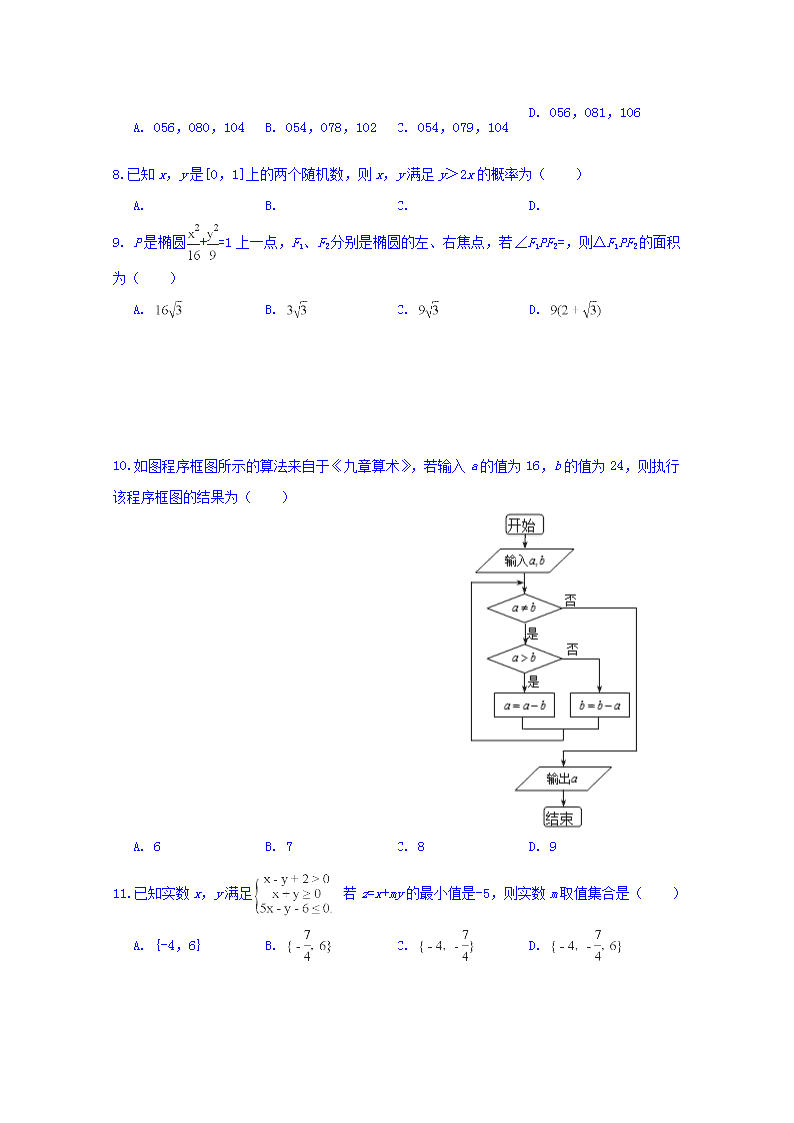
10.如图程序框图所示的算法来自于《九章算术》,若输入a的值为16,b的值为24,则执行该程序框图的结果为( )
A. 6
B. 7
C. 8
D. 9
11.已知实数x,y满足若z=x+my的最小值是-5,则实数m取值集合是( )
A. {-4,6}
B.
C.
D.
12.已知A,B是椭圆E:+=1(a>b>0)的左、右顶点,M是E上不同于A,B的任意一点,若直线AM,BM的斜率之积为-,则E的离心率为( )
A.
B.
C.
D.
(第二卷)
二、 填空题(本大题共4小题,共20分)
13. 焦点在(-2,0)和(2,0),经过点(2,3)的椭圆方程为 ______ .
14. 命题“∃t∈R,t2-2t-a<0”是假命题,则a的取值范围是_____________.
15. 关于x的不等式x2-2ax-3a2<0(a>0)的解集为(x1,x2),且|x1-x2|=8,则a= ______ .
16.某设备的使用年限x与所支出的维修费用y的统计数据如表:
使用年限x(单位:年)
2
3
4
5
6
维修费用y(单位:万元)
1.5
4.5
5.5
6.5
7.0
根据表可得回归直线方程为=1.3x+,据此模型预测,若使用年限为14年,估计维修费用约为 ______ 万元.
三、 解答题(本大题共6小题,共70分)
17.(本题10分)已知p:方程x2+mx+1=0有两个不相等的实根,q:不等式x+-2>0在x∈[2,+∞)上恒成立,若¬p为真命题,p∨q为真命题,求实数m的取值范围.
18.(本题12分)如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,求证:
(1)AE∥平面BDF;
(2)平面BDF⊥平面ACE.
19. (本题12分)已知,,且.
(Ⅰ)试将y表示为x的函数f(x),并求f(x)的单调递增区间;
(Ⅱ)已知a、b、c分别为△ABC的三个内角A、B、C对应的边长,若,且,a+b=6,求△ABC的面积.
20.(本题12分)20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,60)的学生中任选2人,求这两人的成绩都在[60,70)中的概率.
成绩(分)
50 60 70 80 90 100
7a
6a
3a
2a
O
21.(本题12分)已知数列{an}的前n项和为Sn,且Sn=2an-2(n=1,2,3…),(an≠0),数列{bn}中,b1=1,点P(bn,bn+1)在直线x-y+2=0上.
(1)求数列{an},{bn}的通项an和bn;
(2)设cn=an•bn,求数列{cn}的前n项和Tn.
22 (本题12分)已知椭圆C:+=1(a>b>0)的两个焦点分别为F1,F2,离心率为,过F1的直线l与椭圆C交于M,N两点,且△M F1F2的周长为6.
(1)求椭圆C的方程;
(2)若直线y=kx+m与椭圆C分别交于A,B两点,且OA⊥OB,试问点O到直线AB的距离是否为定值,证明你的结论.
高二期中考试理科数学试题
答案和解析
【答案】
一、选择题:1. C 2. B 3. C 4. B 5.D 6. A 7. D 8.A 9. B 10. C 11. B 12. D
二、填空题:13. 14. (-∞,-1] 15. 2 16. 18。
三、解答题:
17.已知p:方程x2+mx+1=0有两个不相等的实根,q:不等式x+-2>0在x∈[2,+∞)上恒成立,若¬p为真命题,p∨q为真命题,求实数m的取值范围.
解:p:方程x2+mx+1=0有两个不相等的实根,
则△=m2-4>0,解得m<-2或m>2;
q:不等式x+-2>0在x∈[2,+∞)上恒成立,
即m>-x2+2x在x∈[2,+∞)上恒成立,
设f(x)=-x2+2x,则f(x)=-(x-1)2+1,
当x=2时,f(x)取得最大值为f(2)=0;
所以m>0;
又¬p为真命题,则p为假命题,所以-2≤m≤2;
由p为假命题,p∨q为真命题知q为真命题,
所以m的取值范围是(0,2].
18.(本题12分)如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,求证:
(1)AE∥平面BDF;
(2)平面BDF⊥平面ACE.
证明:(1)设AC∩BD=G,连接FG,易知G是AC的中点,∵F是EC中点,由三角形中位线的性质可得 FG∥AE,
∵AE⊄平面BFD,FG⊂平面BFD,∴AE∥平面BFD.
(2)∵平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB∴BC⊥平面ABE,又∵AE⊂平面ABE,∴BC⊥AE,
又∵AE⊥BE,BC∩BE=B,∴AE⊥平面BCE,∴AE⊥BF.
在△BCE中,BE=CB,F为CE的中点,∴BF⊥CE,AE∩CE=E,∴BF⊥平面ACE,
又BF⊂平面BDF,∴平面BDF⊥平面ACE.
19.(本题12分)已知,,且.
(Ⅰ)试将y表示为x的函数f(x),并求f(x)的单调递增区间;
(Ⅱ)已知a、b、c分别为△ABC的三个内角A、B、C对应的边长,若,且,a+b=6,求△ABC的面积.
成绩(分)
50 60 70 80 90 100
7a
6a
3a
2a
O
解:(Ⅰ)向量,,
∵
∴,
∴==2sin.
,
则,
故f(x)的单调递增区间为,k∈Z.
成绩(分)
50 60 70 80 90 100
7a
6a
3a
2a
O
(Ⅱ)∵,
∴
∴
∵
由余弦定理:c2=a2+b2-2abcosC,
可得:(a+b)2-3ab=24,
∵a+b=6,
∴ab=4.
故得△ABC的面积S=.
20.(本题12分)20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,60)的学生中任选2人,求这两人的成绩都在[60,70)中的概率.
解:(1)根据直方图知组距=10,由(2a+3a+6a+7a+2a)×10=1,解得a=0.005.
(2)成绩落在[50,60)中的学生人数为2×0.005×10×20=2,
成绩落在[60,70)中的学生人数为3×0.005×10×20=3.
(3)记成绩落在[50,60)中的2人为A,B,成绩落在[60,70)中的3人为C,D,E,
则成绩在[50,70)的学生任选2人的基本事件有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个,
其中2人的成绩都在[60,70)中的基本事件有CD,CE,DE共3个,
故所求概率为P=
21.(本题12分)已知数列{an}的前n项和为Sn,且Sn=2an-2(n=1,2,3…),(an≠0),数列{bn}中,b1=1,点P(bn,bn+1)在直线x-y+2=0上.
(1)求数列{an},{bn}的通项an和bn;
(2)设cn=an•bn,求数列{cn}的前n项和Tn.
解:(1)∵Sn=2an-2,当n≥2时,Sn-1=2an-1-2,…(2分)
由an=Sn-Sn-1=2an-2an-1,
∵an≠0,则∴.…(3分)
∵a1=S1,∴a1=2a1-2,即a1=2,
∴,
∵点P(bn,bn+1)在直线x-y+2=0上,
∴bn-bn+1+2=0,
∴bn+1-bn=2,即数列{bn}是等差数列,又b1=1,
∴bn=2n-1…(6分)
(II)∵…(7分)
,
∴
因此:,…(10分)
即:∴,
∴.
22 (本题12分)已知椭圆C:+=1(a>b>0)的两个焦点分别为F1,F2,离心率为,过F1的直线l与椭圆C交于M,N两点,且△M F1F2的周长为6.
(1)求椭圆C的方程;
(2)若直线y=kx+m与椭圆C分别交于A,B两点,且OA⊥OB,试问点O到直线AB的距离是否为定值,证明你的结论.
解:(1)由题意知,2a+2c=6,
由椭圆离心率e===,则c=1,a=2,b2=3.
∴椭圆C的方程;
(2)由题意,当直线AB的斜率不存在,此时可设A(x0,x0),B(x0,-x0).又A,B两点在椭圆C上,
∴,
∴点O到直线AB的距离,
当直线AB的斜率存在时,设直线AB的方程为y=kx+m.设A(x1,y1),B(x2,y2)
联立方程,消去y得(3+4k2)x2+8kmx+4m2-12=0.
由已知△>0,x1+x2=-,x1x2=,
由OA⊥OB,则x1x2+y1y2=0,即x1x2+(kx1+m)(kx2+m)=0,
整理得:(k2+1)x1x2+km(x1+x2)+m2=0,
∴.
∴7m2=12(k2+1),满足△>0.
∴点O到直线AB的距离d===为定值.
综上可知:点O到直线AB的距离d=为定值.