- 187.00 KB
- 2021-04-20 发布
2018-2019学年黑龙江省双鸭山市第一中学高一下学期期末考试数学(文)试题
一.选择题 (每小题5分,满分60分)
1.在△ABC中,角A,B,C所对的边分别为a,b,c,若B=60°,a=1,b=2,则sin A=( )
A. B. C. D.
2.已知向量a=(1,-2),b=(2m,1),若a⊥b,则m的值为( )
A.-1 B.1 C. - D.
3.等差数列{an}中,a3=2,a5=7,则a7=( )
A.10 B.20 C.16 D.12
4.球O是棱长为2的正方体的内切球,则这个球的体积为 ( )
A. B. C. D.
5.已知a>b,则下列不等式成立的是( )
A.a2>b2 B. C. D.
6.已知m,n是两条不同直线,α,β,γ是三个不同平面,下面命题正确的是( )
A.若α⊥γ,β⊥γ,则α∥β B.若m⊥α,n⊥α,则m∥n
C.若m∥α,n∥α,则m∥n D.若m∥α,m∥β,则α∥β
7.已知a>0,b>0,a+b=1,则y=+的最小值是( )
A. B.4 C.9 D.5
8.在正方体中,若是的中点,则直线垂直于( )
A. B. C. D.
9.在△ABC中,已知sin2A+sin2B-sinAsinB=sin2C,且满足ab=4,则△ABC的面积为( )
A.1 B.2 C. D.
10.大衍数列,来源于《乾坤普》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两翼数量总和,是中国传统文化中隐藏着的世界数学史上第一道数列题.其前项依次是0,2,4, 8,12,18,24,32,40,50,……则此数列的第项为( )
A. B. C. D.
11.在正四棱柱ABCD-A′B′C′D′中,AB=1,A′A=2,则AC′与BC所成角的余弦值为( )
A. B. C. D.
12.已知,且,,这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则( )
A.7 B.6 C.5 D.9
二.填空题(每小题5分,满分20分)
13.已知向量的夹角为60°,=2,=1,则=______.
14.在上定义运算,则不等式的解集为__________.
15.现用一半径为,面积为的扇形铁皮制作一个无盖的圆锥形容器(假定衔接部分及铁皮厚度忽略不计,且无损耗),则该容器的容积为_________.
16.已知六棱锥PABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB.则下列命题中正确的有___________.(填序号)
①PA⊥AD;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④直线PD与平面ABC所成角为30°.
三.解答题 (共70分)
17.(10分)设等比数列{an}的前n项和为Sn.已知a2=6,6a1+a3=30,求an和Sn.
18.(12分)若不等式的解集是.
(1)求的值;
(2)当为何值时,的解集为R.
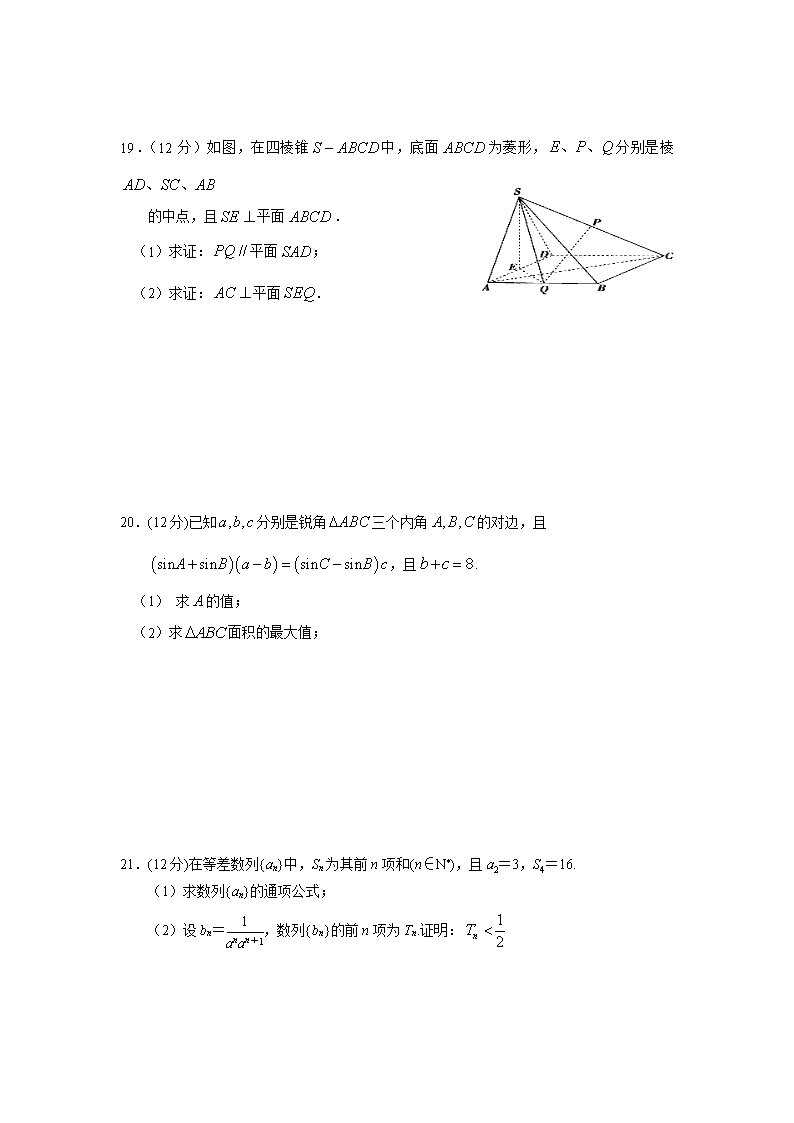
19.(12分)如图,在四棱锥中,底面为菱形,分别是棱
的中点,且平面.
(1)求证:平面;
(2)求证:平面.
20.(12分)已知分别是锐角三个内角的对边,且,且.
(1) 求的值;
(2)求面积的最大值;
21.(12分)在等差数列{an}中,Sn为其前n项和(n∈N*),且a2=3,S4=16.
(1)求数列{an}的通项公式;
(2)设bn=,数列{bn}的前n项为Tn.证明:
22. (12分)如图,在四棱锥P-ABCD中,PA底面ABCD,ADAB,AB//CD,AD=DC=AP=2,AB=1,
点E为棱PC 的中点.
(1)证明:BECD;
(2)求三棱锥P-BDE的体积.
高二期末数学(文)答案
一. 选择题
1- -6.CBDACB 7--12.CBDAAC
二. 填空题
13.1 14.(-4,1) 15. 16.
三.解答题
17.解:设{an}的公比为q,由题设得
解得或
当a1=3,q=2时,an=3×2n-1,Sn=3(2n-1);
当a1=2,q=3时,an=2×3n-1,Sn=3n-1.
18.(1) (2)
19.【解析】证明:(1)取中点,连接.∵分别是棱的中点,
∴,且.∵在菱形中,是的中点,
∴,且,∴且.∴为平行四边形,
∴.∵平面,平面,∴平面.
(2)连接,∵是菱形,∴,
∵分别是棱的中点,∴,∴,
∵平面,平面,∴,
∵,平面,∴平面
20.解: (Ⅰ)因为,由正弦定理有,既有,由余弦定理得, .
(Ⅱ),即,当且仅当时等号成立,
当时, ,
所以的最大值为.
21.解:(1)设等差数列{an}的公差是d,由已知条件得
解得a1=1,d=2,∴an=2n-1.
(2)由(1)知,an=2n-1,
∴bn===,
Tn=b1+b2+…+bn==
22.(1)由已知条件可证,得,可证;
(2)