- 993.00 KB
- 2021-04-20 发布
舒城中学2019-2020学年度第一学期期末考试
高二理数
(总分:150分 时间:120分钟)
第I卷
一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合要求的,请你将符合要求的项的序号填在括号内)
1.命题“”的否定是 ( )
A. B. C. D.
2.抛物线的焦点坐标为 ( )
A. B. C. D.
3.已知,则“且”是“”的 ( )
A.充要条件 B.必要非充分条件 C.充分非必要条件 D.既非充分也非必要条件
4.从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是 ( )
A.“至少有1个白球”和“都是红球” B.“至少有2个白球”和“至多有1个红球”
C.“恰有1个白球” 和“恰有2个白球” D.“至多有1个白球”和“都是红球”
5.掷两颗均匀的骰子,则点数之和为5的概率等于 ( )
A. B. C. D.
6.方程表示的曲线为 ( )
A.一个圆 B.半个圆 C.两个半圆 D.两个圆
7.椭圆的左右焦点分别为,点在椭圆上,若,则( )
A. B. C. D.
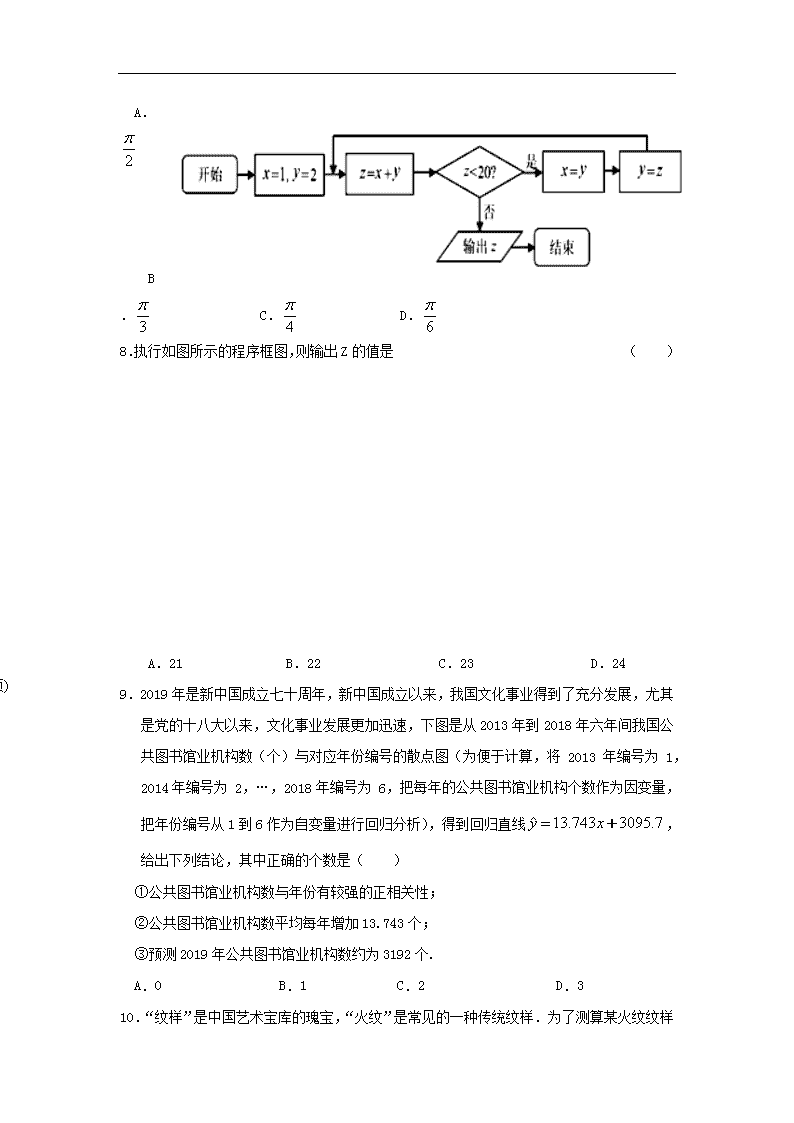
8.执行如图所示的程序框图,则输出Z的值是 ( )
舒中高二期末理数 第1页 (共4页)
A.21 B.22 C.23 D.24
9.2019年是新中国成立七十周年,新中国成立以来,我国文化事业得到了充分发展,尤其是党的十八大以来,文化事业发展更加迅速,下图是从2013 年到 2018 年六年间我国公共图书馆业机构数(个)与对应年份编号的散点图(为便于计算,将 2013 年编号为 1,2014年编号为 2,…,2018年编号为 6,把每年的公共图书馆业机构个数作为因变量,把年份编号从1到6作为自变量进行回归分析),得到回归直线,给出下列结论,其中正确的个数是( )
①公共图书馆业机构数与年份有较强的正相关性;
②公共图书馆业机构数平均每年增加13.743个;
③预测2019年公共图书馆业机构数约为3192个.
A.0 B.1 C.2 D.3
10.“纹样”是中国艺术宝库的瑰宝,“火纹”
是常见的一种传统纹样.为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为5的正方形将其包含在内,并向该正方形内随机投掷1000个点,己知恰有400个点落在阴影部分,据此可估计阴影部分的面积是( )
A.2 B.3 C.10 D.15
11.已知空间三点坐标分别为,又点在平面ABC内,则的值 ( )
A. B.1 C.10 D.11
12.已知:函数,、为其图像上任意两点,则直线的斜率的最小值为 ( )
A. B. C. D.
第Ⅱ卷
二.填空题(本大题共4小题,每小题5分,共20分,请你将正确的答案填在空格处)
13.总体由编号为01,02,03,...,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列开始由左向右读取,则选出来的第5个个体的编号为__________.
78 16 65 72 08 02 63 14 07 02 43 69 69 38 74
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01
14.在上随机地取一个数,则事件“直线与圆相交”发生的概率为_________.
15.双曲线的左、右焦点分别是,过作倾斜角为的直线交双曲线右支于点,若垂直于轴,则双曲线的离心率为 .
16.已知,若且,则
的取值范围为__________.
三.解答题(本大题共6小题,共70分.请你注意解答本题时,一定要详细地写出文字说明、证明过程及演算步骤等)
17.(本大题满分10分)已知命题甲:关于的不等式的解集为实数集,命题乙:关于的方程有两个不相等的实根.
(1)若甲、乙都是真命题,求实数的取值范围;
(2)若甲、乙中至少有一个是真命题,求实数的取值范围.
18.(本大题满分12分20090423
)已知动圆过定点,且与直线相切.
(1)求动圆圆心的轨迹的方程;
(2)设是轨迹上异于原点的两个不同点,直线和的斜率分别为,且,证明直线恒过定点,并求出该定点的坐标
19.(本大题满分12分)如图,在四棱锥中,底面是矩形,是的中点,平面,且,.
(1)求证:;
(2)求与平面所成角的正弦值;
(3)求二面角的余弦值.
舒中高二期末理数 第4页 (共4页)
20.(本大题满分12分)某城市户居民的月平均用电量(单位:度),以
,,,,,,分组的频率分布直方图如图.
(1)求直方图中的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,,,的四组用户中,用分层抽样的方法抽取户居民,则月平均用电量在的用户中应抽取多少户?
21.(本题满分12分)已知函数,.
(1)求函数图像在点处的切线方程;
(2)若不等式对于任意的均成立,求实数的取值范围.
22.(本大题满分12分)如图,椭圆的离心率为,其左焦点到点的距离为,不过原点的直线与椭圆相交于两点,且线段被直线平分.
(1)求椭圆的方程;
(2)求面积取最大值时直线的方程.
舒城中学2019~2020学年度第一学期期末
舒城中学 高 班 姓名 考号
高二数学试卷
(总分:150分 时间:120分钟)
第I卷
一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合要求的,请你将符合要求的项的序号填在括号内)
1.命题“”的否定是( C )
A. B. C. D.
2.抛物线的焦点坐标为( B )
A. B. C. D.
3.已知,则“且”是“”的( C )
A.充要条件 B.必要非充分条件 C.充分非必要条件 D.既非充分也非必要条件
4.从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是( C )
A.“至少有1个白球”和“都是红球” B.“至少有2个白球”和“至多有1个红球”
C. “恰有1个白球” 和“恰有2个白球” D.“至多有1个白球”和“都是红球”
5.掷两颗均匀的骰子,则点数之和为5的概率等于( B )
A. B. C. D.
6.方程表示的曲线为( C )
A.一个圆 B.半个圆 C.两个半圆 D.两个圆
7.椭圆的左右焦点分别为,点在椭圆上,若,则( A )
A. B. C. D.
8.执行如图所示的程序框图,则输出Z的值是( A )
A.21 B.22 C.23 D.24
9.2019年是新中国成立七十周年,新中国成立以来,我国文化事业得到了充分发展,尤其是党的十八大以来,文化事业发展更加迅速,下图是从2013 年到 2018 年六年间我国公共图书馆业机构数(个)与对应年份编号的散点图(为便于计算,将2013 年编号为 1,2014 年编号为 2,…,2018年编号为 6,把每年的公共图书馆业机构个数作为因变量,把年份编号从 1 到 6 作为自变量进行回归分析),得到回归直线,
给出下列结论,其中正确的个数是( D )
①公共图书馆业机构数与年份有较强的正相关性;
②公共图书馆业机构数平均每年增加13.743个;
③预测2019年公共图书馆业机构数约为3192个.
A.0 B.1 C.2 D.3
10.“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样.为了
测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为5的正方形将其
包含在内,并向该正方形内随机投掷1000个点,己知恰有400个点落在阴影
部分,据此可估计阴影部分的面积是( C )
A.2 B.3 C.10 D.15
11.已知空间三点坐标分别为,又点在平面ABC内,则的值 ( D )
A. B.1 C.10 D.11
12.已知:函数,、为其图像上任意两点,则直线的斜率的最小值为( B )
A. B. C. D.
第Ⅱ卷
二.填空题(本大题共4小题,每小题5分,共20分,请你将正确的答案填在空格处)
13.总体由编号为01,02,03,...,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列开始由左向右读取,则选出来的第5个个体的编号为____43______.
78 16 65 72 08 02 63 14 07 02 43 69 69 38 74
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01
14.在上随机地取一个数,则事件“直线与圆相交”发生的概率为_________.
15.双曲线的左、右焦点分别是,过作倾斜角为的直线交双曲线右支于点,若垂直于轴,则双曲线的离心率为 .
16.已知,若且,则的取值范围__.
三.解答题(本大题共6小题,共70分.请你注意解答本题时,一定要详细地写出文字说明、证明过程及演算步骤等)
17.(本大题满分10分)已知命题甲:关于的不等式的解集为实数集,命
题乙:关于的方程有两个不相等的实根.
(1)若甲、乙都是真命题,求实数的取值范围;
(2)若甲、乙中至少有一个是真命题,求实数的取值范围.
17.(1) (2)a>1或a<-4
【详解】
命题甲:由题得
命题乙:由题得或.
(1)若甲、乙都是真命题,所以;
(2)假设甲、乙两个命题都是假命题,甲是假命题,则或,乙是假命题,则,所以.
如果甲、乙中至少有一个是真命题,则a>1或a<4.
18.(本大题满分12分20090423
)已知动圆过定点,且与直线相切.
(1)求动圆圆心的轨迹的方程;
(2)设是轨迹上异于原点的两个不同点,直线和的斜率分别为,且,证明直线恒过定点,并求出该定点的坐标
【解析】(1)设为动圆圆心,为记为,过点作直线的垂线,垂足为,
由题意知:即动点到定点与定直线的距离相等,
由抛物线的定义知,点的轨迹为抛物线,其中为焦点,为准线,
所以轨迹方程为;
(2)如图,设,由题意得,
由题意知直线的斜率存在,从而设AB方程为,显然,
将与联立消去,得
由韦达定理知
由,即
将①式代入上式整理化简可得:,
所以AB方程为过定点.
19.(本大题满分12分)如图,在四棱锥中,底面是矩形,是的中点,平面,且,.
(1)求证:;
(2)求与平面所成角的正弦值;
(3)求二面角的余弦值.
(1) 略 ……………………………………………… ……4分
(2) ∵是矩形,
∴,
又∵平面,
∴,,即,,两两垂直,
∴以为原点,,,分别为轴,轴,轴建立如图空间直角坐标系,
由,,得,,,,,,
则,,,
设平面的一个法向量为,
则,即,令,得,,
∴,
∴,
故与平面所成角的正弦值为.………………………………8
()由()可得,
设平面的一个法向量为,
则,即,令,得,,
∴,
∴,
故二面角的余弦值为.……………………12分
20.(本大题满分12分)某城市户居民的月平均用电量(单位:度),以,,,,,,分组的频率分布直方图如图.
(1)求直方图中的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,,,的四组用户中,用分层
抽样的方法抽取户居民,则月平均用电量在的用户中应抽取多少户?
20.(1);(2),;(3).
【解析】
试题分析:(1)由直方图的性质可得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1,解方程可得;(2)由直方图中众数为最高矩形上端的中点可得,可得中位数在[220,240)内,设中位数为a,解方程(0.002+0.0095++0.011)×20+0.0125×(a-220)=0.5可得;(3)可得各段的用户分别为25,15,10,5,可得抽取比例,可得要抽取的户数
试题解析:(1)由直方图的性质可得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1得:
x=0.0075,所以直方图中x的值是0.0075. ------------- 3分
(2)月平均用电量的众数是=230. ------------- 5分
因为(0.002+0.0095+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240)内,
设中位数为a,
由(0.002+0.0095+0.011)×20+0.0125×(a-220)=0.5
得:a=224,所以月平均用电量的中位数是224. ------------ 8分
(3)月平均用电量为[220,240]的用户有0.0125×20×100=25户,
月平均用电量为[240,260)的用户有0. 0075×20×100=15户,
月平均用电量为[260,280)的用户有0. 005×20×100=10户,
月平均用电量为[280,300]的用户有0.0025×20×100=5户, -------------10分
抽取比例==,所以月平均用电量在[220,240)的用户中应抽取25×=5户.-- 12分
21.(本题满分12分)已知函数,.
(1)求函数图像在点处的切线方程;
(2)若不等式对于任意的均成立,求实数的取值范围.
21.(1)………………4分
(2)………………12分
22.(本大题满分12分)如图,椭圆的离心率为,其左焦点到点的距离为,不过原点的直线与椭圆相交于两点,且线段被直线平分.
(1)求椭圆的方程;
(2)求面积取最大值时直线的方程.
22. (1) …………………………4分
(2) …………………………12分