数学文卷·2019届江西省铅山一中高二上学期第二次月考（2017-12） 10页

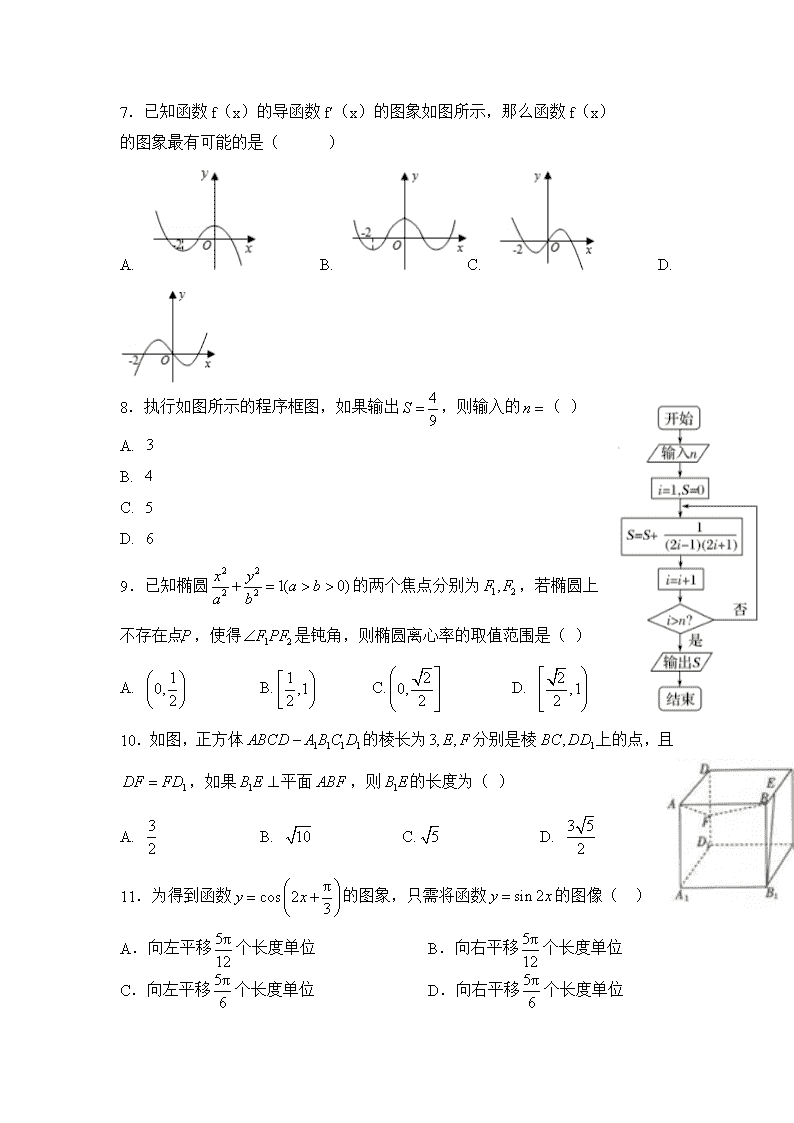
铅山一中2017—2018学年度第一学期第二次月考高二年级 文科数学试卷 分值：150分 考试时间：120分钟 命题人：徐悠林 审题人：郭干军 一、单选题（每小题5分，共12小题，60分）‎ ‎1．已知集合，集合，则（ ）‎ A. B. C. D. ‎ ‎2．设向量与垂直，则等于(　　)‎ A. B. C. 0 D. －1‎ ‎3．在等比数列中，和是方程的两个根，则（ ）‎ A. B. C. D. ‎ ‎4．设,则的概率为 A. B. C. D. ‎ ‎5．设变量满足约束条件，则的最小值为（ ）‎ A. 14 B. 10 C. 6 D. 4‎ ‎6．某几何体的三视图如图所示，则该几何体的体积为（ ）‎ A. ‎ B. ‎ C. ‎ D. ‎ ‎7．已知函数f（x）的导函数f′（x）的图象如图所示，那么函数f（x）‎ 的图象最有可能的是（ ）‎ A. B. C. D. ‎ ‎8．执行如图所示的程序框图，如果输出，则输入的（ ）‎ A. ‎ B. ‎ C. ‎ D. ‎ ‎9．已知椭圆的两个焦点分别为，若椭圆上不存在点，使得是钝角，则椭圆离心率的取值范围是（ ）‎ A. B. C. D. ‎ ‎10．如图，正方体的棱长为分别是棱上的点，且，如果平面，则的长度为（ ）‎ A. B. C. D. ‎ ‎11．为得到函数的图象，只需将函数的图像（ ）‎ A．向左平移个长度单位 B．向右平移个长度单位 C．向左平移个长度单位 D．向右平移个长度单位 ‎12．已知函数f(x)=在上是增函数，则的取值范围是（ ）‎ A. B. C. D. ‎ 二、填空题(每空5分，共20分)‎ ‎13．设向量=（4，m），=（1，-2），且，则|=__________．‎ ‎14．设函数的导数为，且，则 .‎ ‎15．曲线在点处的切线方程为__________．‎ ‎16．已知，数列满足，则__________．‎ 三.解答题 ‎17．（10分）在△ABC中，角的对边分别为，且.‎ ‎(1)求；‎ ‎(2)若，△ABC的面积为，求△ABC的周长.‎ ‎18．（12分）已知数列的前项和满足，其中 ‎（1）求数列的通项公式；‎ ‎（2）设，求数列的前项和.‎ ‎19．（12分）中国神舟十一号载人飞船在酒泉卫星发射中心成功发射，引起全国轰动．开学后，某校高二年级班主任对该班进行了一次调查，发现全班60名同学中，对此事关注的占，他们在本学期期末考试中的物理成绩（满分100‎ 分）如下面的频率分布直方图：‎ ‎（1）求“对此事关注”的同学的物理期末平均分．‎ ‎（2）若物理成绩不低于80分的为优秀，请以是否优秀为分类变量，‎ ‎①补充下面的列联表：‎ 物理成绩优秀 物理成绩不优秀 合计 对此事关注 对此事不关注 合计 ‎②是否有以上的把握认为“对此事是否关注”与物理期末成绩是否优秀有关系？‎ 参考公式：，其中.‎ 参考数据：‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎20．（12分）如图，三棱柱中，底面为正三角形，底面，且，是的中点.‎ ‎（1）求证：平面；‎ ‎（2）求证：平面平面；‎ ‎（3）在侧棱上是否存在一点，使得三棱锥的体积是？若存在，求出的长；若不存在，说明理由.‎ ‎21．（12分）已知函数 .‎ ‎（1）当时，求函数 的极小值；‎ ‎（2）若函数在上为增函数，求的取值范围.‎ ‎22．（12分）已知椭圆，其长半轴为，离心率为.‎ ‎（1）求椭圆的方程.‎ ‎（2）直线经过定点，且与椭圆交于两点，求面积的最大值.‎ 铅山一中2017—2018学年度第一学期第二次月考高二年级 文科数学试卷答案 ‎1．A 2．B 3．C 4．D 5．C 6．B 7．A 8．B 9．C 10．D 11.A 12．D 二、填空题 ‎13．2 14．6 15. 16．2018‎ 三、 解答题 ‎17．（1）；（2）‎ ‎【解析】(1)由，得.‎ 由正弦定理可得.‎ 因为，所以.因为，所以. ‎ ‎(2)因为，所以，又，所以，所以或，则的周长为. ‎ ‎18．(1)（）；(2).‎ 试题解析：（1）∵（），①‎ 当时，，∴， 当时，∵，②‎ ‎①②：，即：（） 所以是等比数列， ∴（）‎ ‎（2）， ∴‎ ‎∴ ∴‎ ‎19．（1）；（2）列联表见解析，没有.‎ 试题解析：（1）对此事关注的同学的物理期末平均分为 ‎（分）．‎ ‎（2）①补充的列联表如下：‎ 物理成绩优秀 物理成绩不优秀 合计 对此事关注 ‎8‎ ‎12‎ ‎20‎ 对此事不关注 ‎8‎ ‎32‎ ‎40‎ 合计 ‎16‎ ‎44‎ ‎60‎ ‎②由①中的列联表可得 ‎，‎ 所以没有以上的把握认为“对此事是否关注”与物理期末成绩是否优秀有关系．‎ ‎20．（1）见解析；（2）见解析；（3）‎ 试题解析：‎ ‎（1）如图,连接交于点，连。‎ 由题意知,在三棱柱中,平面, ‎ ‎∴四边形为矩形, ∴点为的中点.‎ ‎∵ 为的中点, ∴.‎ ‎∵ 平面,平面. ∴ 平面.‎ ‎（2）∵底面为正三角形,是的中点, ∴, ‎ ‎∵ 平面,平面, ∴ .‎ ‎∵ , ∴ 平面,‎ ‎∵ 平面, ∴平面平面.‎ ‎（3）假设在侧棱上存在一点,使三棱锥的体积是.‎ 设。‎ ‎∵ ,,‎ ‎∴ ,‎ 即, 解得, 即.‎ ‎∵ ,‎ ‎∴ 在侧棱上存在一点,使得三棱锥的体积是,此时.‎ ‎21．（1）（2）‎ 试题解析：‎ ‎（1）定义域为．‎ 当时，，．‎ 令，得．‎ 当时，，为减函数；‎ 当时，，为增函数．‎ 所以函数的极小值是．‎ ‎（2）由已知得．‎ 因为函数在是增函数，所以对任意恒成立，‎ 由得，即对任意的恒成立．　‎ 设，要使“对任意恒成立”，只要.‎ 因为，令，得．‎ 当时，，为减函数；‎ 当时，，为增函数．　‎ 所以的最小值是．‎ 故函数在是增函数时，实数的取值范围是．‎ ‎22．（1），；（2）1‎ 试题解析：解：（Ⅰ），，，‎ ‎∴椭圆的方程为：，‎ ‎（Ⅱ）依题意知直线的斜率存在，设直线的斜率为，则直线方程为：，‎ 由，得，‎ ‎，‎ 由得：，‎ 设，，则 ‎，，‎ ‎，‎ 又∵原点到直线的距离，‎ ‎∴‎ ‎．‎ 当且仅当，即时，等号成立，‎ 此时面积的最大值为．‎