- 511.50 KB
- 2021-04-20 发布
山东省菏泽二中2010-2011学年高一数学必修三学分认定考试试卷
一、选择题:
1.给出以下四个问题:
①输入一个数, 输出它的相反数 ②求面积为的正方形的周长
③输出三个数中的最大数 ④求函数的函数值
其中不需要用条件语句来描述其算法的有 ( )
A 个 B 个 C 个 D 个
i=6
s=0
WHILE ①
s=s+i
②
END
PRINT s
END
(第3题)
x=-1
y=20
IF x<0 THEN
x=y+3
ELSE
y=y-3
END IF
PRINT x-y ;y+x
END
(第2题)
2.图中程序运行后输出的结果为( )
(A)3 43 (B) 43 3
(C)-18 16 (D)16 -18
3.条件语句的一般形式如右所示,其中B表示的是( )
A.条件 B.条件语句
C.满足条件时执行的内容 D.不满足条件时执行的内容
4. 某校有40个班,每班50人,每班派3人参加“学代会”,在这个问题中样本容量是( )
A.40 B.50 C.120 D.150
5.在统计中,样本的标准差可以近似地反映总体的( )
A.平均状态 B.分布规律 C.波动大小 D.最大值和最小值
6.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”。根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是()
(A)甲地:总体均值为3,中位数为4
(B)乙地:总体均值为1,总体方差大于0
(C)丙地:中位数为2,众数为3
(D)丁地:总体均值为2,总体方差为3
7.用随机数表法从100名学生(男生25人)中抽选20人进行评教,某男学生被抽到的机率是( )
A. B. C. D.
8.某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为. ()k.s.5.u.c.o.m
(A)9 (B)18 (C)27 (D) 36
9.A 袋中有5个白球和3个黑球,从其中任取2个球,则取得二球颜色不相同的概率是( )
A.0.357 B.0.107 C.0.646 D.0.250
10. 某家庭电话,打进的电话响第一声时被接的概率为,响第二声时被接的概率为,响第三声时被接的概率为,响第四声时被接的概率为,则电话在响前四声内被接的概率为( )
A. B. C. D.
11. 将一颗质地均匀的骰子(它是一种各面上分别标有点数1,2,3,4,5,6的正方体玩具)先后抛掷3次,至少出现一次6点向上的概率是( )
A. B. C. D.
12. 从分别写有A、B、C、D、E的5张卡片中,任取2张,这2张上的字母恰好按字母顺序相邻的概率为( )
A. B. C. D.
二、填空题
开始
?
是
输入p
结束
输出
否
13.执行下方的程序框图,若,则输出的
(13题) (14题)
14.样本容量为200的频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在内的频数为 ,估计样本的众数为 ,中位数为 ,
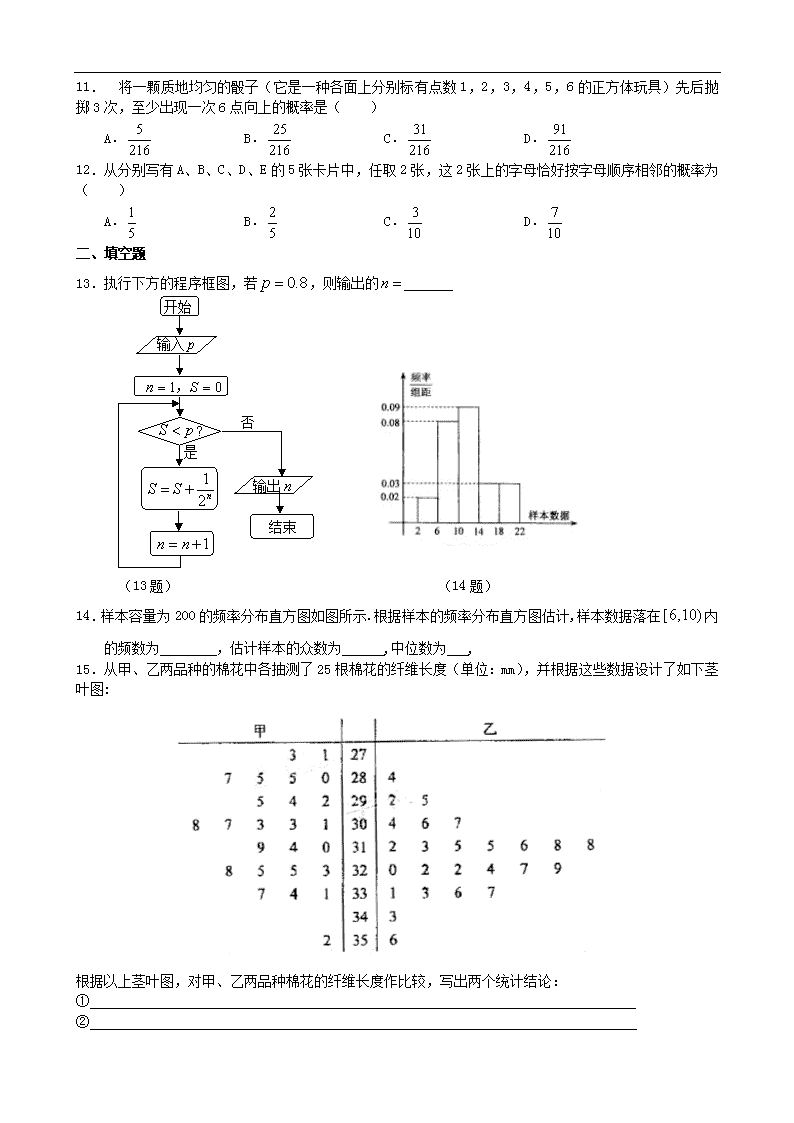
15.从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),并根据这些数据设计了如下茎叶图:
根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论:
①
②
16.A 某市电话号码为6位数,则电话号码由6个不同数字组成的概率是_________.
三、解答题
17 从甲、乙、丙、丁四个人中选两名代表,求:
(1)甲被选中的概率
(2)丁没被选中的概率
18 现有一批产品共有件,其中件为正品,件为次品:
(1)如果从中取出一件,然后放回,再取一件,求连续次取出的都是正品的概率;
(2)如果从中一次取件,求件都是正品的概率
19 某路公共汽车分钟一班准时到达某车站,求任一人在该车站等车时间
少于分钟的概率(假定车到来后每人都能上)
20. 一个路口的红绿灯,红灯的时间为秒,黄灯的时间为秒,绿灯的时间为
秒,当你到达路口时看见下列三种情况的概率各是多少?
(1) 红灯 (2) 黄灯 (3) 不是红灯
21.甲﹑乙两人玩一种游戏,每次有甲﹑乙两人各出1到5根手指,若和为偶数则甲赢,否则乙赢。
(1)若以A表示和为6的事件,求P(A)
(2)这种游戏公平吗?试说明理由。
22.一汽车厂生产A,B,C三类轿车,每类轿车有舒适型和标准型两种型号,每月的产量如下表(单位:辆):
轿车A
轿车B
轿车C
舒适型
100
150
Z
标准型
300
450
600
按类型分层抽样的方法在这个厂生产的轿车中抽取50辆,其中A类轿车10辆。
(1) 求z的值。
(2) 用分层抽样的方法在C类轿车中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率。
(3) 用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,
9.2, 9.6, 8.7,9.3, 9.0,8.2。把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率。