- 2.92 MB
- 2021-04-20 发布
山东省济南市2019-2020学年高二下学期末考试试题
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知复数,其中i为虚数单位,则z的共轭复数是
2.展开式中的常数项为
A. 120 B.70 C.20 D. 1
3.正方体中,
4.已知某种动物由出生算起活到20岁的概率为0.8,活到25岁的概率为0.4,则现为20岁的这种动物活到25岁的概率是
A. 0.6 B. 0.5 C.0.4 D. 0.32
5.曲线在点(0,f(0))处的切线方程为
A.y=2
В. y =2x
C.y=x+2
D. y =-x+2
6·若随机变量,则D(2X+1)=
7.若对任意的恒成立,则实数a的最小值是
A.2 B.3 C.4 D.5
8.《山东省高考改革试点方案》规定: 2020年高考总成绩由语文、数学、外语三门统考科目和思想政治、历史、地理、物理、化学、生物六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为A、B+,B、C+、C、D+、D、E共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%,7%,16%,24%,24%、16%.7%,3%,选考科目成绩计人考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100], [81,90],[71,80]、[61,70]、[51,60]、[41,50]、[31,40].[21,30]八个分数区间,得到考生的等级成绩,如果山东省某次高考模拟考试物理科目的原始成绩X~ N(50,256),那么D等级的原始分最高大约为
附:①若,则Y~N(0,1) ;
②当Y~N(0,1)时,.
A. 23 B. 29 C.36 D. 43
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求全部选对得5分;部分选对的得3分;有选错的得0分.
9.已知复数,其中i是虚数单位,则下列结论正确的是
A.
B.的虚部为
C.
D.在复平面内对应的点在第四象限
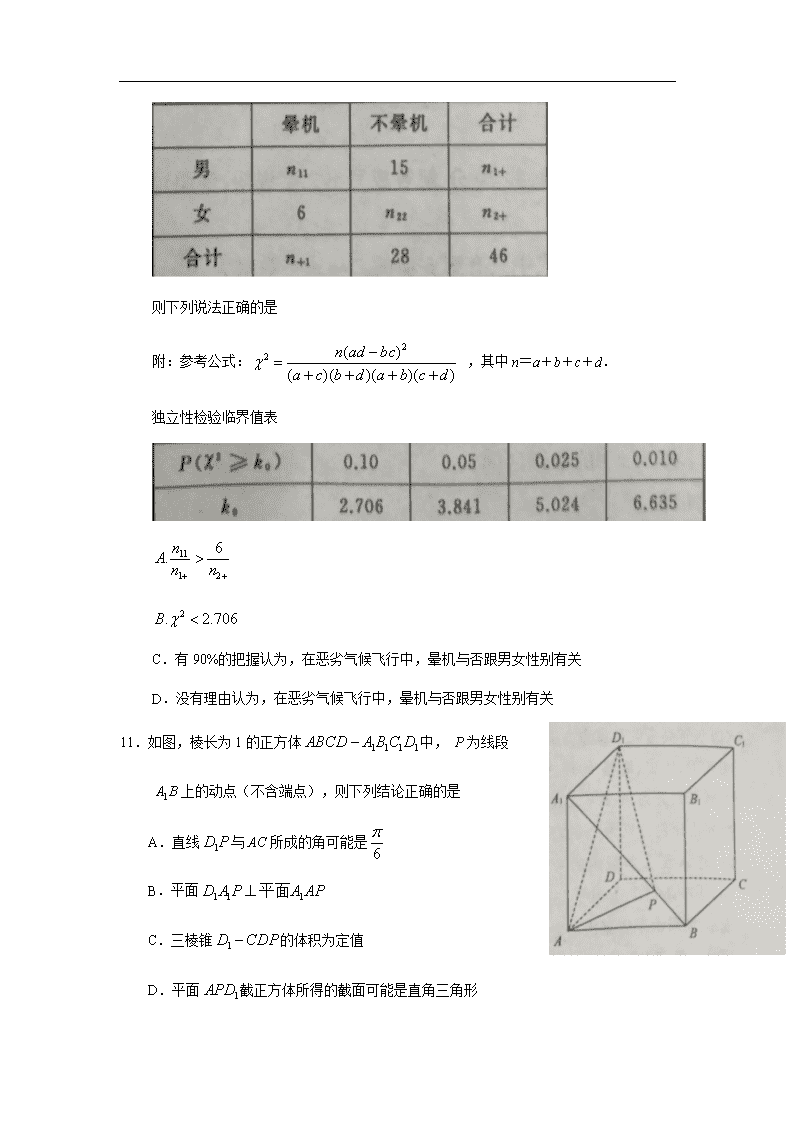
10.在一次恶劣气候的飞行航程中,调查男女乘客在机上晕机的情况,如下表所示:
则下列说法正确的是
附:参考公式: ,其中n=a+b+c+d.
独立性检验临界值表
C.有90%的把握认为,在恶劣气候飞行中,晕机与否跟男女性别有关
D.没有理由认为,在恶劣气候飞行中,晕机与否跟男女性别有关
11.如图,棱长为1的正方体中, P为线段
上的动点(不含端点),则下列结论正确的是
A.直线与AC所成的角可能是
B.平面
C.三棱锥的体积为定值
D.平面截正方体所得的截面可能是直角三角形
12.已知函数,则下列结论正确的是
A、存在,使得
B. a=1时,点(0,-1)是函数f(x)图象的对称中心
C.b<0时,f(x)在R上存在减区间
D.b<0时,若f(x)有且仅有两个零点,且,则
三、填空题:本题共4小题,每小题5分,共20分.
13.已知向量 ,且,则λ的值为________
14.某老师安排甲、乙、丙、丁4名同学从周一至周五值班,每天安排1人,每人至少1天,若甲连续两天值班,则不同的安排方法种数为________.(请用数字作答)
15.如图,正三棱柱的底面边长为2,侧棱长为2,则AC1与面ABB1A1所成的角为________.
16.甲乙两名同学进行羽毛球比赛,采用三局两胜制,甲每局获胜的概率为p,甲赢得比赛的概率为q.若q>p,则p的取值范围是________;当
q-p取得最大值时, p的值为________(本题第一空2分,第二空3分)
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)
已知展开式中只有第5项的二项式系数最大.
(1)求展开式中含的项;
(2)设,求的值
18.(12分)
已知函数.
(1)当a=2时,求f(x)的单调区间;
(2)求f(x)的极值
19.(12分)
某学校组织一次自然科学夏令营活动,有10名同学参加,其中有6名男生、4名女生,为了活动的需要,要从这10名同学中随机抽取3名同学去采集自然标本.
(1)已知10名同学中有2名共青团员,求抽取的3人中至少有1名共青团员的概率;
(2)设X表示抽取的3名同学中女生的人数,求X的分布列及数学期望.
20.(12分)
如图,三棱锥D—ABC中,AD=BD=, AB=2,,AC⊥平面ABD, AE⊥BC于点E.
(1)求证:BD ⊥平面ACD;
(2)求二面角C—AE—D的余弦值
21.(12分)
自新型冠状病毒肺炎(COVID—19)疫情爆发以来,国家采取了强有力的措施进行防控,并及时通报各项数据以便公众了解情况,做好防护.以下是济南市2020年1月24月~
31日的累计确诊人数统计表与对应的散点图.将1月24日作为第1天,连续8天的时间作为变量x,每天累计确诊人数作为变量y.
(1)由散点图知,变量y与x具有较强的线性相关关系,求y关于x的回归直线方程;
(2)经过医学研究,发现新型冠状病毒极易传染,如果每一个健康个体被感染的概率为0.3,在一次9人的家庭聚餐中,有一位感染者参加了聚餐,记其余8人中被感染的人数为X,求P(X=k)取得最大值时k的值.
参考公式及数据:
22.(12分)
已知函数.
(1)若,求f(x)的最值;
(2)若存在,使得 ,求实数m的取值范围.