- 751.00 KB
- 2021-04-20 发布
5月9日半月考文数试题
范围:选填:集合逻辑,函数基本性质 解答题:高考全部内容
一、单选题(每题5分,共60分)
1.集合, ,则( )
A. B. C. D.
2.下列命题中,真命题是( )
A., B.,
C.的充要条件是 D.,是的充分条件
3.已知命题:,;命题:,,则下列命题为真命题的是( )
A. B. C. D.
4.已知条件,条件,则是的( )
A充分不必要条件 B必要不充分条件 C充要条件 D.既不充分也不必要
5.命题“,使成立”的否定为( )
A.,使成立 B.,使成立
C.,均有成立 D.,均有成立
6.已知是定义在R上的奇函数,当时(m为常数),则的值为( ) A.4 B.6 C. D.
7.下列说法中,正确的是 ( )
A.幂函数的图象都经过点(1,1)和点(0,0)
B.当a=0时,函数y=xα的图象是一条直线
C.若幂函数y=xα的图象关于原点对称,则y=xα在定义域内y随x的增大而增大
D.幂函数y=xα,当a<0时,在第一象限内函数值随x值的增大而减小
8.函数与的图象关于直线________对称。
A. B. C. D.
9.将函数的图象向右平移一个单位长度,所得图象与曲线关于直线对称,则( )
A. B. C. D.
10.已知是定义是上的奇函数,满足,当时, ,则函数在区间上的零点个数是( )
A.3 B.5 C.7 D.9
11.函数的部分图像大致为( )
A. B.C. D.
12.已知函数,若,则( )
A. B. C. D.
二、填空题(每题5分,共20分)
13.函数的图像恒经过的定点是________.
14.已知命题“若,则”,命题的原命题,逆命题,否命题,逆否命题中真命题的个数为 .
15.已知函数是奇函数,且时,有,,则不等式的解集为____.
16.16.定义域为的奇函数,当时,,则关于的方程所有根之和为,则实数的值为________
三、解答题
17.(12分)在中,内角所对的边分别为,且.
(1)求角; (2)若,的面积为,求的值.
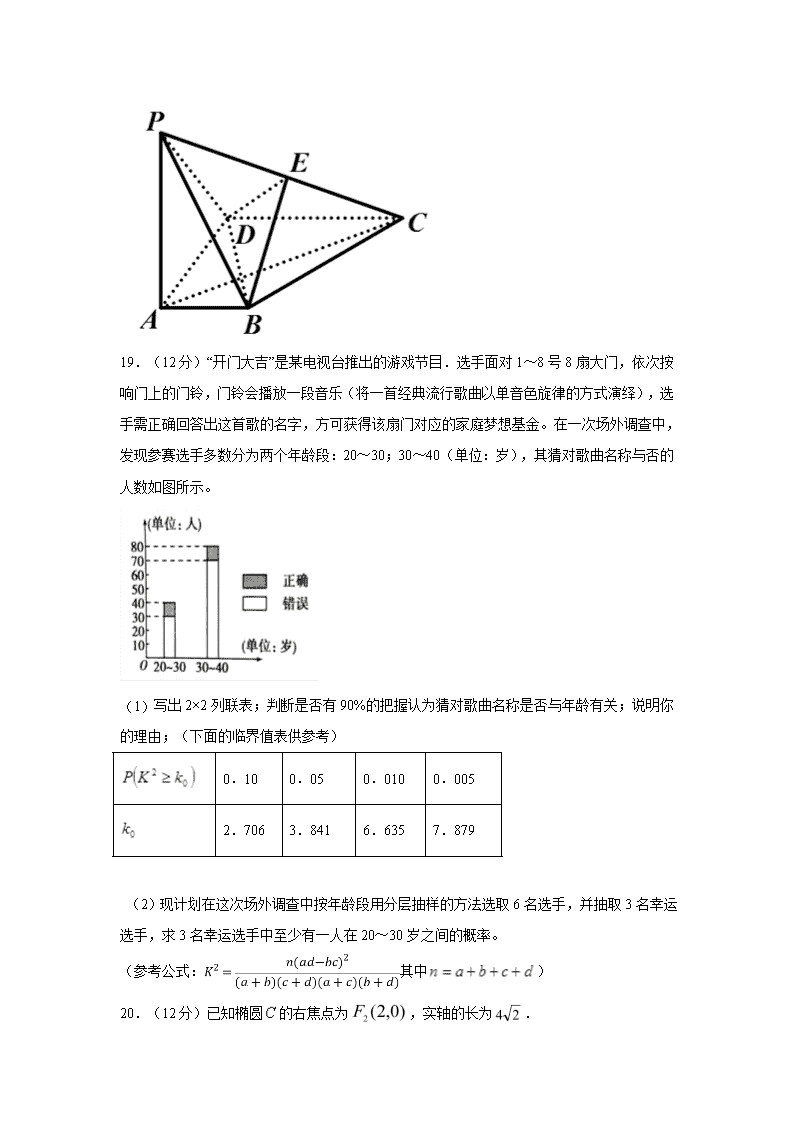
18.(12分)如图,在四棱锥中, 底面, , ,点为棱的中点.
(1)证明: 面; (2)求三棱锥的体积.
19.(12分)“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金。在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示。
(1) 写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称是否与年龄有关;说明你的理由;(下面的临界值表供参考)
0.10
0.05
0.010
0.005
2.706
3.841
6.635
7.879
(2)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,并抽取3名幸运选手,求3名幸运选手中至少有一人在20~30岁之间的概率。
(参考公式:其中)
20.(12分)已知椭圆的右焦点为,实轴的长为.
(1)求椭圆的标准方程;
(2)过点作两条互相垂直的直线分别交椭圆于点和,求的最小值.
21.(12分)已知函数.
(1)求曲线在点处的切线方程;
(2)若在区间上恒成立,求的取值范围.
22.(10分)在直角坐标系中,直线的参数方程是(为参数).以坐标原点为极点,以轴的正半轴为极轴,建立极坐标系,曲线的极坐标方程是.(1)求直线的普通方程和曲线的直角坐标方程;
(2)设点,若直线与曲线交于, 两点,且,求实数的值.
参考答案
1.D
3.D
5.D
6.C
7.D
8.A
9.C
10.D
11.D
12.C
13.
14.2
15.
16.
17.(1)可通过化简计算出的值,然后解出的值。
( 2)可通过计算和的值来计算的值。
【详解】
(1)由得,
又,所以,得,所以。
(2)由的面积为及得,即 ,
又,从而由余弦定理得,所以,
所以。
18.证明:(1)取中点,连接
分别是的中点
四边形是平行四边形
又
(2) .
19.(1)由图可知,年龄段在20~30(单位:岁),其中猜对10人,猜错30人,年龄段在30~40(单位:岁),其中猜对10人,猜错70人,故可列出2×2列联表,根据参考公式可算出,
故有的把握认为猜对歌曲名称与否和年龄有关。(2)首先确定这是个古典概型,通过列举可知从6人中取3人的结果有20种,而事件A的结果有16种,故3名幸运选手中至少有一人在20~30岁之间的概率。
试题解析:(1)
年龄/正误
正确
错误
合计
20~30
10
30
40
30~40
10
70
80
合计
20
100
120
由上表可知
有的把握认为猜对歌曲名称与否和年龄有关。
(2)设事件A为3名幸运选手中至少有一人在20~30岁之间,由已知得20~30岁之间的人数为2人,30~40岁之间的人数为4人,从6人中取3人的结果有20种,事件A的结果有16种,故3名幸运选手中至少有一人在20~30岁之间的概率
20.(1)由题可知:椭圆的焦点在轴上,其标准方程可设为:
又实轴的长为,则,;,故.
故椭圆的标准方程为: 4分
(2)由题可知:
1°当或所在的直线斜率为零时,另一条直线的斜率不存在,
此时= 6分
2°当与所在的直线斜率都存在,而且不为零时,设所在直线的斜率为,则所在的直线斜率为.
则所在直线方程为:.
联立得:,即.
设两点的横坐标分别为则由韦达定理可得:
8分
则=
=
=
以代换上式中的可得:
10分
则+
令,则.此时
.由二次函数的性质可得:.故.
此时,即.
综上可知:当时取得最小值,最小值为. 13分
21.(1)因为f(x)=exsinx-ax2,
所以f¢(x)=ex(cosx+sinx)-2ax,
故f¢(0)=1.
又f(0)=0,
故所求切线方程为y= x.
(2)①当x=0时,f(0)=0在区间上恒成立.
②当0<x≤时,由得在上恒成立.
令g(x)=,x∈(0, ],
则g¢(x)=.
令G(x)=x(sinx+cosx)-2sinx,x∈(0, ],
则G¢(x)=(cosx-sinx)(x-1),
故当0<x<时,G¢(x)<0,G(x)单调递减;
当<x<1时,G¢(x)>0,G(x)单调递增;
当1<x≤时,G¢(x)<0,G(x)单调递减,
又G(0)=0,G(1)=cos1-sin1<0,
所以G(x)<0,
所以g¢(x)<0,
所以g(x)在(0, ]上单调递减,
所以g(x)≥g()=,
故a≤.
综上实数的取值范围为.
22.(1)直线的参数方程是(为参数),
消去参数可得直线的普通方程为
曲线的极坐标方程是,化为,
所以曲线的直角坐标方程为.
(2)将(为参数)代入方程,
得.
即.由,解得,所以
∵,∴,解得或或1,
都满足,所以或或.