- 1.69 MB
- 2021-04-20 发布
定州市2018—2019学年度第一学期期中考试
高二数学(理科)试题
命题人:常少朋
说明:本试卷分为第Ⅰ卷和第Ⅱ卷两部分,共三个大题,22个小题。满分150分,时间120分钟。Ⅰ卷答案涂在答题卡上或答在第Ⅱ卷前相应的表格中。交卷时只收第Ⅱ卷。
第Ⅰ卷(客观题 共60分)
一.选择题:本大题共12小题,每小题5分,共60分。在下列各题的四个选项中,只有一个选项是符合要求的。
1.若命题“p或q”为真,“非p”为真,则( )
A.p真q真 B.p假q假 C.p假q真 D.p真q假
2.抛物线的焦点坐标是( )
A. B. C. D.
3.下列命题正确的是( )
A. 命题p:对任意的x∈R,x2+x+1>0,则Øp:对任意的x∈R,x2+x+1≤0
B. 在△ABC中,角A,B,C的对边分别是a,b,c,则a>b是cos A<cos B的充要条件
C. 已知p:>0,则Øp:≤0
D. 存在实数x∈R,使sin x+cos x=成立
4.《朗读者》以精美的文字,最平实的情感读出文字背后的价值,感染了众多听众,中央电视台在2018年推出了《朗读者第二季》,电视台节目组要从2018名观众中抽取50名幸运观众.先用简单随机抽样从2018人中剔除18人,剩下的2000人再按系统抽样方法抽取50人,则在2018人中,每个人被抽取的可能性 ( )
A. 都相等,且为 B. 都相等,且为
C. 均不相等 D. 不全相等
5.从装有个红球和个黑球的口袋内任取个球,那么互斥而不对立的两个事件是( )
A.至少有一个黑球与都是红球 B.恰有一个黑球与恰有两个黑球
C.至少有一个黑球与至少有一个红球 D.至少有一个黑球与都是红球
6.已知左、右焦点分别为,的双曲线上一点P,满足|PF1|=17,则( )
A.1或33 B.1 C.33 D.1或11
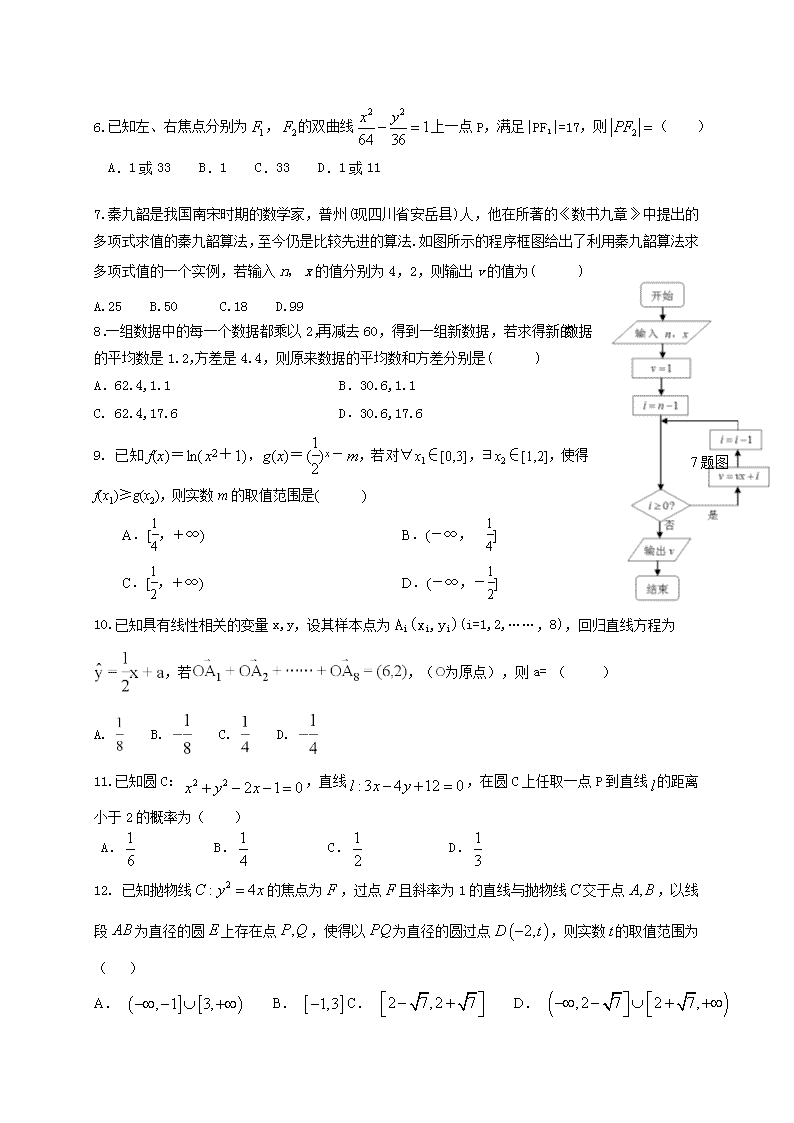
7.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )
A.25 B.50 C.18 D.99
8.一组数据中的每一个数据都乘以2,再减去60,得到一组新数据,若求得新的数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是( )
A.62.4,1.1 B.30.6,1.1
C. 62.4,17.6 D.30.6,17.6
7题图
9. 已知f(x)=ln(x2+1),g(x)=()x-m,若对∀x1∈[0,3],∃x2∈[1,2],使得f(x1)≥g(x2),则实数m的取值范围是( )
A.[,+∞) B.(-∞, ]
C.[,+∞) D.(-∞,-]
10.已知具有线性相关的变量x,y,设其样本点为Ai(xi,yi)(i=1,2,……,8),回归直线方程为,若,(为原点),则a= ( )
A. B. C. D.
11.已知圆C:,直线,在圆C上任取一点P到直线的距离小于2的概率为( )
A. B. C. D.
12. 已知抛物线的焦点为,过点且斜率为1的直线与抛物线交于点,以线段为直径的圆上存在点,使得以为直径的圆过点,则实数的取值范围为( )
A. B. C. D.
第Ⅱ卷(主观题 共90分)
二. 填空题(每小题5分,共20分)
13.若k进制数132(k)与二进制数11110(2)相等.则k= .
14.已知两定点,,若直线上存在点,使得,则实数的取值范围是 .
15.已知M是椭圆上任意一点,F为其左焦点,点A为圆C:(x+1)2+(y−10)2=1上任意一点,则|MA|-|MF|的最小值是
16.抛物线的焦点为,点在抛物线上,且,弦的中点在准线上的射影为,则的最大值为
三.解答题(6小题,共60分)
17.(本小题满分10分)
已知设成立; 指数函数为增函数,如果“”为真,“”为假,求实数的取值范围.
18.(本小题满分12分)
在同一平面内,动点M与两定点A1(-a,0)、A2(a,0)(a>0)连线的斜率之积等于非零常数m,加上A1、A2两点所成的曲线C,求曲线C的方程,并讨论C的形状与m值的关系;
19(本小题满分12分)
2018年10月23日,习近平宣布大桥正式开通;大桥于10月24日上午9时正式通车;这座被誉为“新世界七大奇迹”的大桥,问鼎多项“世界之最”:世界上总体跨度最长、钢结构桥体最长、海底沉管隧道最长的跨海大桥;是公路建设史上技术最复杂、施工难度最高、工程规模最庞大的桥梁,世界最大尺寸高阻尼橡胶隔震支座、世界最大难度深水无人对接的沉管隧道等等…,现在在定州市中学生中,对这座世纪大桥的了解程度进行调查,随机选取了100人进行问卷调查,并将问卷中的这100人根据其了解度评分值百分制按照[50,60),[60,70),……,[90,100)分成5组,制成如图所示频率分直方图.
(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知了解度评分值在[50,60)内的男生数与女生数的比为3:2,若在了解度评分值为[50,60)的人中随机抽取2人进行问答,求恰有1名女生的概率.
20.(本小题满分12分)
是否存在同时满足下列两条件的直线:
(1)与抛物线有两个不同的交点A和B;(2)线段AB被直线:垂直平分.
若存在,求出直线的方程,若不存在,说明理由。
21.(本小题满分12分)
某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前五年平均每台设备每年的维护费用大致如下表:
年份t(年)
1
2
3
4
5
维护费y(万元)
1.1
1.5
1.8
2.2
2.4
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)若该设备的价格是每台5万元,甲认为应该使用满五年换一次设备,而乙则认为应该使用满十年换一次设备,你认为甲和乙谁更有道理?并说明理由.
(参考公式:,)
22. (本小题满分12分)
已知椭圆的左、右焦点分别为,离心率为,双曲线方程为,直线与双曲线的交点为且.
(Ⅰ)求椭圆与双曲线的方程;
(Ⅱ)过点的直线与椭圆交于两点,交双曲线于两点,当的内切圆的面积取最大值时,求的面积.
定州市2018—2019学年度第一学期期中考试
理科试题答案
一.选择题
1 .C 2.B 3.B 4.A 5.B 6.C 7.B 8.B 9.A 10.B 11.B 12.C
二 .填空题
13. 4 14. 15. 16.
三.解答题
17.解:若为真:对, 恒成立,
设,配方得,
所以在上的最小值为,
所以,解得,所以为真时: ; ┉┉┉┉┉┉┉2分
若为真: , ┉┉┉┉┉┉┉4分
因为”为真,“”为假,所以与一真一假, ┉┉┉┉┉┉┉5分
当真假时,所以, ┉┉┉┉┉┉┉7分
当假真时,所以, ┉┉┉┉┉┉┉9分
综上所述,实数的取值范围是或. ┉┉┉┉┉┉┉10分
18.设动点为M,其坐标为(x,y),
当x≠±a时,由条件可得
,
即mx2-y2=ma2(x≠±a), ┉┉┉┉┉┉┉3分
又A1(-a,0)、A2(a,0)的坐标满足mx2-y2=ma2, ┉┉┉┉┉┉┉4分
故依题意,曲线C的方程为mx2-y2=ma2,
当m<-1时,曲线C的方程为,C是焦点在y轴上的椭圆;┉┉┉┉┉6分
当m=-1时,曲线C的方程为x2+y2=a2,C是圆心在原点的圆; ┉┉┉┉┉8分
当-1<m<0时,曲线C的方程为,C是焦点在x轴上的椭圆;┉┉┉┉10分
当m>0时,曲线C的方程为,C是焦点在x轴上的双曲线.┉┉┉┉┉12分
19. 解(1)由(0.005+0.02+0.035+0.030+x)×10=1,解得x =0.01 ┉┉┉┉┉3分
(2)这组数据的平均数为55×0.05+65×0.2+75×0.35+85×0.3+95×0.1=77
中位数设为m,则0.05+0.2+(m-70)×0.035=0.5,解得m= ┉┉┉┉┉7分
(3) 满意度评分值在[50,60)内有100×0.005×10=5人, ┉┉┉┉┉8分
其中男生 3人,女生2人.记为A1,A2,A3,B1,B2,
记“了解度评分值为[50,60)的人中随机抽取2人进行问答,恰有1名女生”为事件A。
通过列举知总基本事件个数为10个,A包含的基本事件个数为6个,┉┉┉┉┉11分
利用古典概型概率公式可知, ┉┉┉┉┉12分
20.假定在抛物线上存在这样的两点
┉┉┉┉3分
∵线段AB被直线:x+5y-5=0垂直平分,
且. ┉┉┉┉┉6分
设线段AB的中点为.代入x+5y-5=0得x=1.
于是:AB中点为. ┉┉┉┉┉9分
故存在符合题设条件的直线,其方程为:
. ┉┉┉┉┉12分
(另法:设直线方程为y=5x+b,与抛物线联立后利用韦达定理,亦可)
21.解: ┉┉┉┉┉┉┉2分
┉┉┉┉┉┉┉5分
┉┉┉┉┉┉┉6分
所以回归方程为 .┉┉┉┉┉┉┉7分
(Ⅱ)若满五年换一次设备,则由(Ⅰ)知每年每台设备的平均费用为:
(万元), ┉┉┉┉┉┉┉9分
若满十年换一次设备,则由(Ⅰ)知每年每台设备的平均费用大概为:
(万元),┉┉┉┉┉┉┉11分
因为,所以甲更有道理. ┉┉┉┉┉┉┉12分
22. 解:(Ⅰ)椭圆:的离心率为,则,┉┉┉┉┉1分
不妨设,由得,,
把代入双曲线方程得,解得, ┉┉┉┉┉3分
所以椭圆方程为.所以双曲线的方程为. ┉┉┉┉┉5分
(Ⅱ)设, 点的坐标分别为,不妨设,内切圆半径.
所以的周长是,
所以, ┉┉┉┉┉6分
所以当圆的半径最大时,面积最大,即, ┉┉┉┉┉7分
设直线的方程为,
,消去得, ┉┉┉┉┉8分
解得,,
所以, ┉┉┉┉┉9分
不妨设,于是,
因为在上单调递增,
所以,
当且仅当时取到.
故直线与椭圆交于两点使得的内切圆的面积最大. ┉┉┉┉┉11分
所以,所以,即,
故的面积为. ┉┉┉┉┉12分