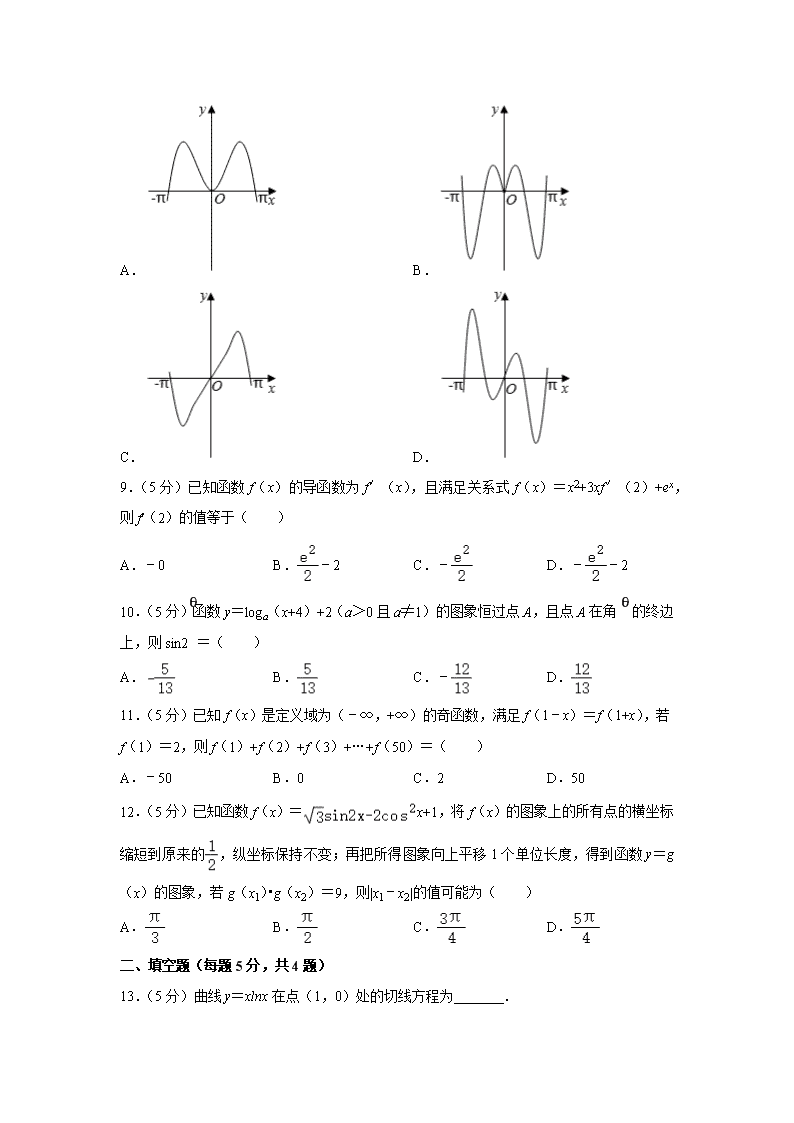- 137.42 KB
- 2021-04-20 发布
2020-2021学年黑龙江省牡丹江一中高三(上)开学
数学试卷(文科)
一、选择题(每题5分,共12题)
1.(5分)设集合A={x|2x>1},B={x||x|≤1},则A∩B=( )
A.(﹣1,1) B.(0,1] C.[﹣1,1] D.[0,1]
2.(5分)设i为虚数单位,复数z满足z(1﹣i)=2i,则|z|=( )
A.1 B. C.2 D.2
3.(5分)命题“∀x∈R,x2﹣x+1>0”的否定是( )
A.∃x∈R,x2﹣x+1≤0 B.∃x∈R,x2﹣x+1<0
C.∀x∈R,x2﹣x+1≤0 D.∀x∈R,x2﹣x+1<0
4.(5分)若sin()=﹣,α为第二象限角,则tanα=( )
A. B. C. D.
5.(5分)已知命题p:“∀x∈[1,e],a>lnx”,命题q:“∃x∈R,x2﹣4x+a=0””若“p∧q”是真命题,则实数a的取值范围是( )
A.(1,4] B.(0,1] C.[﹣1,1] D.(4,+∞)
6.(5分)甲,乙,丙,丁四名学生,仅有一人阅读了语文老师推荐的一篇文章.当它们被问到谁阅读了该篇文章时,甲说:“丙或丁阅读了”;乙说:“丙阅读了”;丙说:“甲和丁都没有阅读”;丁说:“乙阅读了”.假设这四名学生中只有两人说的是对的,那么读了该篇文章的学生是( )
A.甲 B.乙 C.丙 D.丁
7.(5分)设锐角△ABC的三内角A,B,C所对边的边长分别为a,b,c,且b=2,A=2B,则a的取值范围为( )
A. B. C. D.(0,4)
8.(5分)函数y=2|x|sin2x的图象可能是( )
A. B.
C. D.
9.(5分)已知函数f(x)的导函数为f′(x),且满足关系式f(x)=x2+3xf′(2)+ex,则f'(2)的值等于( )
A.﹣0 B.﹣2 C.﹣ D.﹣﹣2
10.(5分)函数y=loga(x+4)+2(a>0且a≠1)的图象恒过点A,且点A在角θ的终边上,则sin2θ=( )
A. B. C.﹣ D.
11.(5分)已知f(x)是定义域为(﹣∞,+∞)的奇函数,满足f(1﹣x)=f(1+x),若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=( )
A.﹣50 B.0 C.2 D.50
12.(5分)已知函数f(x)=x+1,将f(x)的图象上的所有点的横坐标缩短到原来的,纵坐标保持不变;再把所得图象向上平移1个单位长度,得到函数y=g(x)的图象,若g(x1)•g(x2)=9,则|x1﹣x2|的值可能为( )
A. B. C. D.
二、填空题(每题5分,共4题)
13.(5分)曲线y=xlnx在点(1,0)处的切线方程为 .
14.(5分)设函数f(x)=,则f(x)≤3成立的x的取值范围 .
15.(5分)已知,则cos(α﹣β)= .
16.(5分)设函数,若互不相等的实数a,b,c满足f(a)=f(b)=f(c),则2a+2b+2c的取值范围是 .
三、解答题(17题10分,18-22题,每题12分)
17.(10分)已知p:|2x﹣5|≤3,q:x2﹣(a+2)x+2a≤0.
(1)若p是真命题,求对应x的取值范围;
(2)若p是q的必要不充分条件,求a的取值范围.
18.(12分)(文)已知函数f(x)=(sinωx+cosωx)cosωx﹣(ω>0)的最小正周期为4π.
(1)求ω的值;
(2)求f(x)的单调递增区间.
19.(12分)在△ABC中,a,b,c,分别为角A,B,C的对边,且sinB﹣sinC=sin(A﹣C).
(Ⅰ)求角A;
(Ⅱ)若a=3,求b+2c的最大值.
20.(12分)如图,D是直角△ABC斜边BC上一点,AC=DC.
(Ⅰ)若∠BAD=60°,求∠ADC的大小;
(Ⅱ)若BD=2DC,且AB=,求AD的长.
21.(12分)设函数f(x)=x2+1﹣lnx.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求函数g(x)=f(x)﹣x在区间上的最小值.
22.(12分)已知函数f(x)=ax2+(a﹣2)x﹣lnx.
(Ⅰ)若函数f(x)在x=1时取得极值,求实数a的值;
(Ⅱ)当0<a<1时,求f(x)零点的个数.
2020-2021学年黑龙江省牡丹江一中高三(上)开学数学试卷(文科)
参考答案与试题解析
一、选择题(每题5分,共12题)
1.【分析】求出集合A,B,由此能求出A∩B.
【解答】解:∵集合A={x|2x>1}={x|x>0},
B={x||x|≤1}={x|﹣1≤x≤1},
∴A∩B={x|0<x≤1}=(0,1].
故选:B.
2.【分析】把已知等式变形,利用复数代数形式的乘除运算,再由复数模的计算公式求解.
【解答】解:由z(1﹣i)=2i,得z=,
∴|z|=.
故选:B.
3.【分析】命题“∀x∈R,x2﹣x+1>0”是全称命题,其否定应为特称命题,注意量词和不等号的变化.
【解答】解:命题“∀x∈R,x2﹣x+1>0”是全称命题,否定时将量词对任意的x∈R变为∃x∈R,再将不等号>变为≤即可.
故选:A.
4.【分析】由已知求得cosα,进一步得到sinα,再由商的关系求得tanα.
【解答】解:由sin()=﹣,得cos,
∵α为第二象限角,∴sin.
则tanα=.
故选:A.
5.【分析】先求出命题p,q成立的等价条件,利用命题“p∧q”为真命题,确定实数a的取值范围
【解答】解:若命题p:“∀x∈[1,e],a>lnx,为真命题,
则a>lne=1,
若命题q:“∃x∈R,x2﹣4x+a=0”为真命题,
则△=16﹣4a≥0,解得a≤4,
若命题“p∧q”为真命题,
则p,q都是真命题,
则,
解得:1<a≤4.
故实数a的取值范围为(1,4].
故选:A.
6.【分析】先阅读题意,再结合简单的合情推理逐一检验即可得解.
【解答】解:①当读了该篇文章的学生是甲,则四位同学都错了,与题设矛盾,故读了该篇文章的学生不是甲,
②当读了该篇文章的学生是乙,则丙,丁说的是对的,与题设相符,故读了该篇文章的学生是乙,
③当读了该篇文章的学生是丙,则甲,乙,丙说的是对的,与题设矛盾,故读了该篇文章的学生不是丙,
④当读了该篇文章的学生是丁,则甲说的是对的,与题设矛盾,故读了该篇文章的学生不是丁,
综合①②③④得:
读了该篇文章的学生是乙,
故选:B.
7.【分析】由题意可得0<2B<,且<3B<π,解得B的范围,可得cosB的范围,由正弦定理求得a=4cosB,根据cosB的范围确定出a范围即可.
【解答】解:锐角△ABC中,角A、B、C所对的边分别为a、b、c,A=2B,
∴0<2B<,且B+A=3B,
∴<3B<π.
∴<B<,
∴<cosB<,
∵b=2,A=2B,
∴由正弦定理可得:a===4cosB,
∴可得:2<4cosB<2,
则a的取值范围为(2,2).
故选:A.
8.【分析】直接利用函数的图象和性质求出结果.
【解答】解:根据函数的解析式y=2|x|sin2x,得到:函数的图象为奇函数,
故排除A和B.
当x=时,函数的值也为0,
故排除C.
故选:D.
9.【分析】根据导数公式先求出f'(x),然后令x=2即可得到f'(2)的值.
【解答】解:∵f(x)=x2+3xf′(2)+ex,
∴f'(x)=2x+3f'(2)+ex,
令x=2,
则f'(2)=4+3f'(2)+e2,
即﹣2f'(2)=4+e2,
∴f'(2)=﹣﹣2.
故选:D.
10.【分析】令对数的真数等于零,求得x、y的值,可得定点A的坐标,再利用任意角的三角函数的定义求得tanθ,再利用同角三角函数的基本关系、二倍角的正弦公式,求得sin2θ的值.
【解答】解:对于函数y=loga(x+4)+2(a>0且a≠1),令x+4=1,求得x=﹣3,y=2,
可得函数的图象恒过点A(﹣3,2),
且点A在角θ的终边上,∴tanθ==﹣,则sin2θ===﹣,
故选:C.
11.【分析】根据函数奇偶性和对称性的关系求出函数的周期是4,结合函数的周期性和奇偶性进行转化求解即可.
【解答】解:∵f(x)是奇函数,且f(1﹣x)=f(1+x),
∴f(1﹣x)=f(1+x)=﹣f(x﹣1),f(0)=0,
则f(x+2)=﹣f(x),则f(x+4)=﹣f(x+2)=f(x),
即函数f(x)是周期为4的周期函数,
∵f(1)=2,
∴f(2)=f(0)=0,f(3)=f(1﹣2)=f(﹣1)=﹣f(1)=﹣2,
f(4)=f(0)=0,
则f(1)+f(2)+f(3)+f(4)=2+0﹣2+0=0,
则f(1)+f(2)+f(3)+…+f(50)=12[f(1)+f(2)+f(3)+f(4)]+f(49)+f(50)
=f(1)+f(2)=2+0=2,
故选:C.
12.【分析】化函数f(x)为正弦型函数,根据三角函数图象变换写出函数y=g(x)的解析式,利用g(x1)•g(x2)=9求得x1、x2满足的条件,再求|x1﹣x2|的可能取值.
【解答】解:函数f(x)=x+1=sin2x﹣cos2x=2sin(2x﹣),
将f(x)的图象上的所有点的横坐标缩短到原来的倍,得y=2sin(4x﹣)的图象;
再把所得图象向上平移1个单位,得函数y=g(x)=2sin(4x﹣)+1的图象,
若g(x1)•g(x2)=9,则4x﹣=+2kπ,k∈Z;
解得x=+,k∈Z;
其中x1、x2是三角函数g(x)最高点的横坐标,
∴|x1﹣x2|的值为T的整数倍,且T==.
故选:B.
二、填空题(每题5分,共4题)
13.【分析】求出原函数的导函数,得到函数在x=1时的导数值,即切线的斜率,然后由直线方程的点斜式得答案.
【解答】解:由f(x)=xlnx,得
,
∴f′(1)=ln1+1=1,
即曲线f(x)=xlnx在点(1,0)处的切线的斜率为1,
则曲线f(x)=xlnx在点(1,0)处的切线方程为y﹣0=1×(x﹣1),
整理得:x﹣y﹣1=0.
故答案为:x﹣y﹣1=0.
14.【分析】根据f(x)的解析式可看出,x<1时,满足f(x)≤3;x≥1时,由f(x)≤3可得,,从而得出1≤x≤9,这样便可得出x的取值范围.
【解答】解:①∵x<1;
∴x﹣1<0;
∴ex﹣1<1;
∴x<1时,f(x)≤3成立;
②x≥1时,由f(x)≤3得,;
∴x≤9;
∴1≤x≤9;
∴x≤9;
∴x的取值范围为:(﹣∞,9].
故答案为:(﹣∞,9].
15.【分析】已知两等式两边分别平方,利用同角三角函数间的基本关系化简得到关系式,所求式子利用两角和与差的余弦函数公式化简后,把各自的值代入计算即可求出值.
【解答】解:已知等式平方得:(cosα+cosβ)2=cos2α+2cosαcosβ+cos2β=①,
(sinα+sinβ)2=sin2α+2sinαsinβ+sin2β=②,
①+②得:2+2(cosαcosβ+sinαsinβ)=1,
即cosαcosβ+sinαsinβ=﹣,
则cos(α﹣β)=cosαcosβ+sinαsinβ=﹣.
故答案为:﹣
16.【分析】根据题意,做出函数的草图,利用数形结合判断a、b、c
的范围与关系,然后求解2a+2b+2c的取值范围,即可得答案.
【解答】解:根据题意,函数=,其草图如图
若互不相等的实数a,b,c,满足f(a)=f(b)=f(c),
设f(a)=f(b)=f(c)=m,则函数y=f(x)的图象与直线y=m有3个不同的交点,分别为(a,m),(b,m),(c,m),
且0<m<1,
结合函数的图象:有a∈(﹣∞,0),b∈(0,1),c∈(4,5),
当m→1时,表达式2a+2b+2c的值趋向最小值:0+2+24=18,
当m→0时,表达式2a+2b+2c的值趋向最大值:1+1+25=34.
则2a+2b+2c的取值范围是(18,34).
故答案为:(16,34).
三、解答题(17题10分,18-22题,每题12分)
17.【分析】(1)由p:|2x﹣5|≤3是真命题,解含绝对值不等式的性质能求出x的取值范围.
(2)由P:1≤x≤4,q:(x﹣2)(x﹣a)≤0,p是q的必要不充分条件得到:当a≥2时,q:2≤x≤a,当a=2时,q:x=2,当a<2时,q:a≤x≤2,利用分类讨论思想能求出a的取值范围.
【解答】解:(1)∵p:|2x﹣5|≤3是真命题,
∴|2x﹣5|≤3,∴﹣3≤2x﹣5≤3,
解得1≤x≤4,
∴x的取值范围是[1,4].
(2)由(1)知:P:1≤x≤4,
q:x2﹣(a+2)x+2a=(x﹣2)(x﹣a)≤0,
p是q的必要不充分条件
当a≥2时,q:2≤x≤a,故满足a≤4,即2<a≤4,
当a=2时,q:x=2,满足条件;
当a<2时,q:a≤x≤2,故满足a≥1,即1≤a<2.
综上所述a的取值范围是[1,4].
18.【分析】(1)利用三角函数中的恒等变换应用可求得f(x)=sin(2ωx+),利用其最小正周期为4π可求得ω;
(2)由(1)知,f(x)=sin(x+),利用正弦函数的单调性即可求得f(x)的单调递增区间.
【解答】解:(1)∵f(x)=sinωxcosωx+cos2ωx﹣
=sin2ωx+cos2ωx+﹣
=sin(2ωx+),
∵T==4π,
∴ω=.
(2)∵f(x)=sin
∵﹣+2kπ≤x+≤+2kπ,k∈Z
∴﹣π+4kπ≤x≤π+4kπ,k∈Z
∴f(x)的单调递增区间为[﹣+4kπ,+4kπ](k∈Z).
19.【分析】(Ⅰ)由已知利用三角函数恒等变换的应用可求cosA=,进而可求A的值;
(Ⅱ)根据三角函数恒等变换的应用,正弦定理可求可得b+2c=2sin(B+φ),其中tanφ=,φ∈(0,),结合范围B∈(0,),利用正弦函数的性质即可求解.
【解答】解:(Ⅰ)在△ABC中,sinB﹣sinC=sin(A﹣C),
∴sin(A+C)﹣sinC=sin(A﹣C),
即sinAcosC+cosAsinC﹣sinC=sinAcosC﹣cosAsinC
∴2cosAsinC=sinC≠0,
∴cosA=,
∴A=.
(Ⅱ)∵由,
可得b+2c=2(sinB+2sinC)
=2[sinB+2sin(120°﹣B)]
=2(2sinB+cosB)
=2sin(B+φ),其中tanφ=,φ∈(0,),
由B∈(0,),存在B使得B+φ=,
∴sin(B+φ)的最大值为1,
∴b+2c的最大值为2.
20.【分析】(Ⅰ)由已知可求∠DAC=30°,在△ADC中,由正弦定理可得sin∠ADC=,即可解得∠ADC=120°.
(Ⅱ)由已知在△ABC中,由勾股定理可得DC=1,BD=2,AC=,令∠ADB=θ,由余弦定理,即可解得AD的值.
【解答】(本题满分为12分)
解:(Ⅰ)∵∠BAD=60°,∠BAC=90°,
∴∠DAC=30°,…1分
在△ADC中,由正弦定理可得:,…2分
∴sin∠ADC=sin∠DAC=,…3分
∴∠ADC=120°,或60°,…4分
又∠BAD=60°,
∴∠ADC=120°…6分
(Ⅱ)∵BD=2DC,
∴BC=3DC,
在△ABC中,由勾股定理可得:BC2=AB2+AC2,可得:9DC2=6+3DC2,
∴DC=1,BD=2,AC=,…8分
令∠ADB=θ,由余弦定理:
在△ADB中,AB2=AD2+BD2﹣2AD•BD•cosθ,…9分
在△ADC中,AC2=AD2+CD2﹣2AD•CD•cos(π﹣θ),…10分
可得:,
∴解得:AD2=2,可得:AD=…12分
21.【分析】(I)求出导函数,得出函数的单调区间;
(II)求导函数,判断函数在区间上的单调性,然后求出最小值.
【解答】解:(I)f(x)=x2+1﹣lnx∴f'(x)=2x﹣=,
∴当x在(,+∞)时,f'(x)>0,函数递增,
当x在(0,)时,f'(x)<0,函数递减,
故函数的增区间为(,+∞),减区间为(0,);
(II)由g(x)=f(x)﹣x=x2﹣x+1﹣lnx,
得g'(x)=,x∈,令g'(x)=0,则x=1,
∴g(x)在上单调递减,在(1,2]上单调递增,
∴g(x)min=g(1)=1,
∴函数的最小值为1.
22.【分析】( I)求出函数的f(x)定义域为(0,+∞),导函数.通过导函数的符号判断函数的单调性然后求解函数的极值,推出a即可.
( II )令,由0<a<1,得.求出函数的单调区间以及函数的极值,利用函数零点判断定理转化推出结果即可.
【解答】(共14分)
解:( I)f(x)定义域为(0,+∞).
.
由已知,得f'(1)=0,解得a=1.
当a=1时,.
所以f'(x)<0⇔0<x<1,f'(x)>0⇔x>1.
所以f(x)减区间为(0,1),增区间为(1,+∞).
所以函数f(x)在x=1时取得极小值,其极小值为f(1)=0,符合题意
所以a=1.……………………………………………………………………(5分)
( II )令,由0<a<1,得.
所以.
所以f(x)减区间为,增区间为.
所以函数f(x)在时取得极小值,其极小值为.
因为0<a<1,所以.
所以.所以.
因为,
又因为0<a<1,所以a﹣2+e>0.
所以.
根据零点存在定理,函数f(x)在上有且仅有一个零点.
因为x>lnx,f(x)=ax2+(a﹣2)x﹣lnx>ax2+(a﹣2)x﹣x=x(ax+a﹣3).
令ax+a﹣3>0,得.
又因为0<a<1,所以.
所以当时,f(x)>0.
根据零点存在定理,函数f(x)在上有且仅有一个零点.
所以,当0<a<1时,f(x)有两个零点.………………………………(14分)