【数学】西藏自治区林芝市第二高级中学2019-2020学年高一下学期第一学段考试试题（解析版） 8页

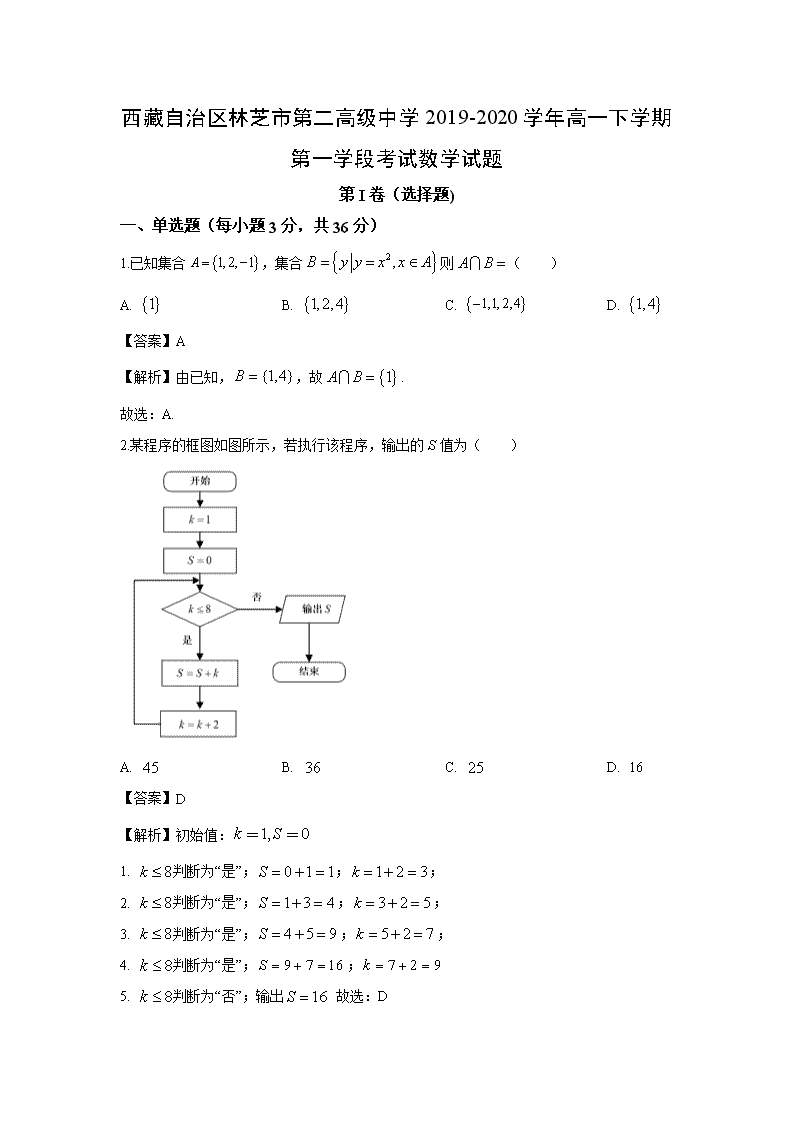
西藏自治区林芝市第二高级中学2019-2020学年高一下学期第一学段考试数学试题 第I卷（选择题)‎ 一、单选题（每小题3分，共36分）‎ ‎1.已知集合，集合则（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】由已知，，故.‎ 故选：A.‎ ‎2.某程序的框图如图所示，若执行该程序，输出的值为（ ）‎ ‎ ‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】初始值：‎ ‎1. 判断为“是”；；；‎ ‎2. 判断为“是”；；；‎ ‎3. 判断为“是”；；；‎ ‎4. 判断为“是”；；‎ ‎5. 判断为“否”；输出 故选：D ‎3.现要完成下列三项抽样调查：①从罐奶粉中抽取罐进行食品安全卫生检查；②高二年级有名学生，为调查学生的学习情况抽取一个容量为的样本；③从某社区户高收入家庭，户中等收入家庭，户低收入家庭中选出户进行消费水平调查.以下各调查方法较为合理的是（ ）‎ A. ①系统抽样，②简单随机抽样，③分层抽样 B. ①简单随机抽样，②分层抽样，③系统抽样 C. ①分层抽样，②系统抽样，③简单随机抽样 D. ①简单随机抽样，②系统抽样，③分层抽样 ‎【答案】D ‎【解析】对于① ,从罐奶粉中抽取罐进行食品安全卫生检查,由于总体数量较少,因此可用简单随机抽样的方法调查.‎ 对于② ,高二年级有名学生,为调查学生学习情况抽取一个容量为的样本.总体数量较多,且对于学生来说,有可以直接使用的学号等编码,所以选择系统抽样调查.‎ 对于③ ,从某社区户高收入家庭,户中等收入家庭,户低收入家庭中选出户进行消费水平调查.调查的各个家庭收入有差距,因而选择分层抽样调查的方法.‎ 综上可知,对三项分别使用的调查方法为: 简单随机抽样; 择系统抽样; 分层抽样.‎ 故选:D ‎4.某校高一学生进行测试，随机抽取名学生的测试成绩，绘制茎叶图如图所示，则这组数据的中位数和众数分别为（ ）‎ A. ， B. ， ‎ C. ， D. ，‎ ‎【答案】D ‎【解析】由茎叶图知：数据为、、、、、、、、、、、、、、、、、、、，‎ 因此，这组数据的众数为，中位数为.‎ 故选：D.‎ ‎5.某人连续投篮2次，事件“至少有1次投中”的对立事件是（ ）‎ A. 恰有1次投中 B. 至多有1次投中 ‎ C. 2次都投中 D. 2次都未投中 ‎【答案】D ‎【解析】某人连续投篮2次，事件“至少有1次投中”的对立事件是：2次都未投中.‎ 故选：D.‎ ‎6.若A，B为对立事件，则下列式子中成立的是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】若事件A与事件B是对立事件，则为必然事件，‎ 再由概率的加法公式得.‎ 故选：D.‎ ‎7.等于（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎8.已知角的终边经过点，则角的正弦值为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】因为角的终边经过点，则，，‎ 所以.‎ 故选：D.‎ ‎9.函数的最小正周期是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】函数的最小正周期是.‎ 故选：A.‎ ‎10.学校有3个文艺类兴趣小组，甲、乙两位同学各自参加其中一个小组，他们参加各个小组的可能性相同，则这两位同学参加同一个文艺类兴趣小组的概率为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】学校有3个文艺类兴趣小组，甲、乙两位同学各自参加其中一个小组，‎ 他们参加各个小组的可能性相同，‎ 基本事件总数n＝3×3＝9.‎ 这两位同学参加同一个文艺类兴趣小组包含的基本事件个数m＝3，‎ 则这两位同学参加同一个文艺类兴趣小组的概率p.‎ 故选：B ‎11.某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为、、、件，为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取件进行检验，则应从丁种型号的产品中抽取（ ）件.‎ A B. C. D. ‎ ‎【答案】A ‎【解析】设应从丁种型号的产品中抽取件，由分层抽样的基本性质可得，解得.‎ 故选：A.‎ ‎12.要得到函数的图象，只需要将函数的图象（ ）‎ A. 向左平移个单位 B. 向右平移个单位 C. 向左平移个单位 D. 向右平移个单位 ‎【答案】B ‎【解析】因为函数，要得到函数的图象，只需要将函数的图象向右平移个单位．‎ 本题选择B选项 第II卷（非选择题)‎ 二、填空题（每小题4分，共16分）‎ ‎13.已知，则____________________________．‎ ‎【答案】‎ ‎【解析】因为，‎ 所以,‎ 故答案为.‎ ‎14.化简：=_____‎ ‎【答案】‎ ‎【解析】‎ ‎，‎ 故答案为.‎ ‎15.已知，则的值是__________.‎ ‎【答案】‎ ‎【解析】由，平方可得.‎ 解得.故答案.‎ ‎16.若，则该函数定义域为_________‎ ‎【答案】‎ ‎【解析】因为，所以，解得，‎ 所以该函数定义域为.‎ 故答案为 三、解答题（共48分）‎ ‎17.在某中学举行的物理知识竞赛中，将三个年级参赛学生的成绩在进行整理后分成5组，绘制出如图所示的须率分布直方图，图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.‎ ‎（1）求成绩在50-70分的频率是多少 ‎（2）求这三个年级参赛学生的总人数是多少：‎ ‎（3）求成绩在80-100分的学生人数是多少 解：（1）成绩在50-70分的频率为：.‎ ‎（2）第三小组的频率为：.‎ 这三个年级参赛学生的总人数（总数=频数/频率）为：（人）‎ ‎（3）成绩在80-100分的频率为：‎ 则成绩在80-100分的人数为：（人）.‎ ‎18.已知，且是第一象限角，求，的值.‎ 解：∵，且是第一象限角 ‎∴，‎ ‎19.某车间有5名工人其中初级工2人，中级工2人，高级工1人现从这5名工人中随机抽取2名．‎ Ⅰ求被抽取的2名工人都是初级工的概率；‎ Ⅱ求被抽取的2名工人中没有中级工的概率．‎ 解：Ⅰ设初级工为，，中级工为，，高级工为c，‎ 从中随机取2人，‎ 基本事件有10个，分别为：‎ ‎，，，，，，，，，．‎ 抽到2名工人都是初级工的情况为：，共1种，‎ 被抽取的2名工人都是初级工的概率．‎ Ⅱ没有抽取中级工的情况有3种，分别为：‎ ‎，，，‎ 被抽取的2名工人中没有中级工的概率．‎ ‎20.化简：‎ ‎（1）；‎ ‎（2）.‎ 解：（1）‎ ‎（2）‎ ‎21.已知函数，求它的振幅、最小正周期、初相.‎ 解：振幅，最小正周期，初相.‎ 故答案为：振幅为2，最小正周期为，初相为.‎