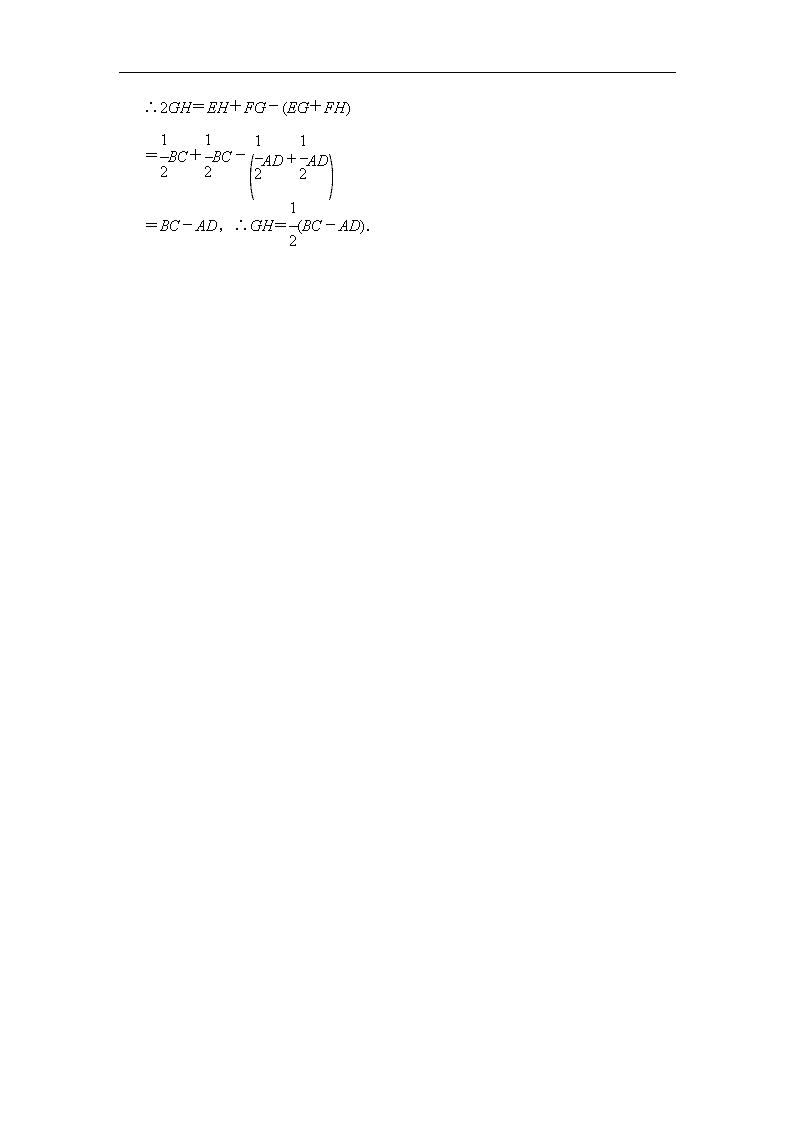高中数学人教a版选修4-1课后习题解答：1-1平行线等分线段定理 2页

第一讲 相似三角形的判定及有关性质 ‎ 第1课时　平行线等分线段定理 习题1.1　(第5页)‎ ‎1．解　如图所示，设AB为待7等分的长为6厘米的线段．‎ 作法　(1)过点A作射线AC；‎ ‎(2)在射线AC上以适当的长度顺次截取AD＝DE＝EF＝FG＝GH＝HK＝KM；‎ ‎(3)连接BM；‎ ‎(4)过D、E、F、G、H、K做BM的平行线，分别交AB于点D′、E′、F′、G′、H′、K′，则D′、E′、F′、G′、H′、K′即为线段AB的7等分点．‎ ‎2．解　猜想：BE＝EF＝FD.‎ 证明：∵M是AB的中点，N是DC的中点，四边形ABCD是平行四边形，∴AM∥CN，且AM＝CN，‎ ‎∴四边形ANCM是平行四边形．‎ ‎∴MC∥AN，∴ME平分BF，即BE＝EF，‎ 同理可证FD＝EF，∴BE＝EF＝FD.‎ ‎3．证明　∵E、F分别是梯形ABCD中AB、DC边上的中点，‎ ‎∴EF∥AD∥BC.‎ ‎∴G、H分别是梯形对角线BD、AC的中点．‎ ‎∴EG＝AD，FH＝AD，EH＝BC，FG＝BC.‎ 又∵GH＝EH－EG，GH＝FG－FH，‎ ‎∴2GH＝EH＋FG－(EG＋FH)‎ ‎＝BC＋BC－ ‎＝BC－AD，∴GH＝(BC－AD)．‎