- 224.50 KB
- 2021-04-20 发布
合肥一六八中学 2018—2019 学年第一学期期中考试
高二数学试题(凌志班)
命题人:史传奇 审题人:朱克洋
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分)
1.下面四个命题:
①分别在两个平面内的两直线是异面直线;
②若两个平面平行,则其中一个平面内的任何一条直线必平行于另一个平面;
③如果一个平面内的两条直线平行于另一个平面,则这两个平面平行;
④如果一个平面内的任何一条直线都平行于另一个平面,则这两个平面平行.
其中正确的命题是( )
A.①② B.②④ C.①③ D.②③
2.过点 且垂直于直线 的直线方程为( )
A. B.
C. D.
3.如图,矩形 O'A'B'C'是水平放置的一个平面图形的直观图,其中 O'A'=3cm,
O'C'=1cm,则原图形的面积是( )
A. B. C. D.6cm2
4.点(4,﹣2)到直线 的距离是( )
A.1 B.2 C. D.6
5.已知空间两条不同的直线 m,n 和两个不同的平面 ,则下列命题中正确的是( )
A.若 B.若
C.若 D.若
6.直线 l 过点 P(1,0),且与以 A(2,1), 为端点的线段总有公共
点,则直线 l 斜率的取值范围是( )
A. B. C. D.[1,+∞)
7.已知 ,则直线 通过( )
,α β
/ / , , / /m n m nα α⊂ 则 , ,m m n nα β α∩ = ⊥ ⊥则
/ / , / / , / /m n m nα α 则 / / , , , / /m m n m nα β α β⊂ = 则
( 1,3)P − 032 =+− yx
012 =−+ yx 052 =−+ yx
052 =−+ yx 072 =+− yx
0, 0ab bc< < ax by c+ =
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
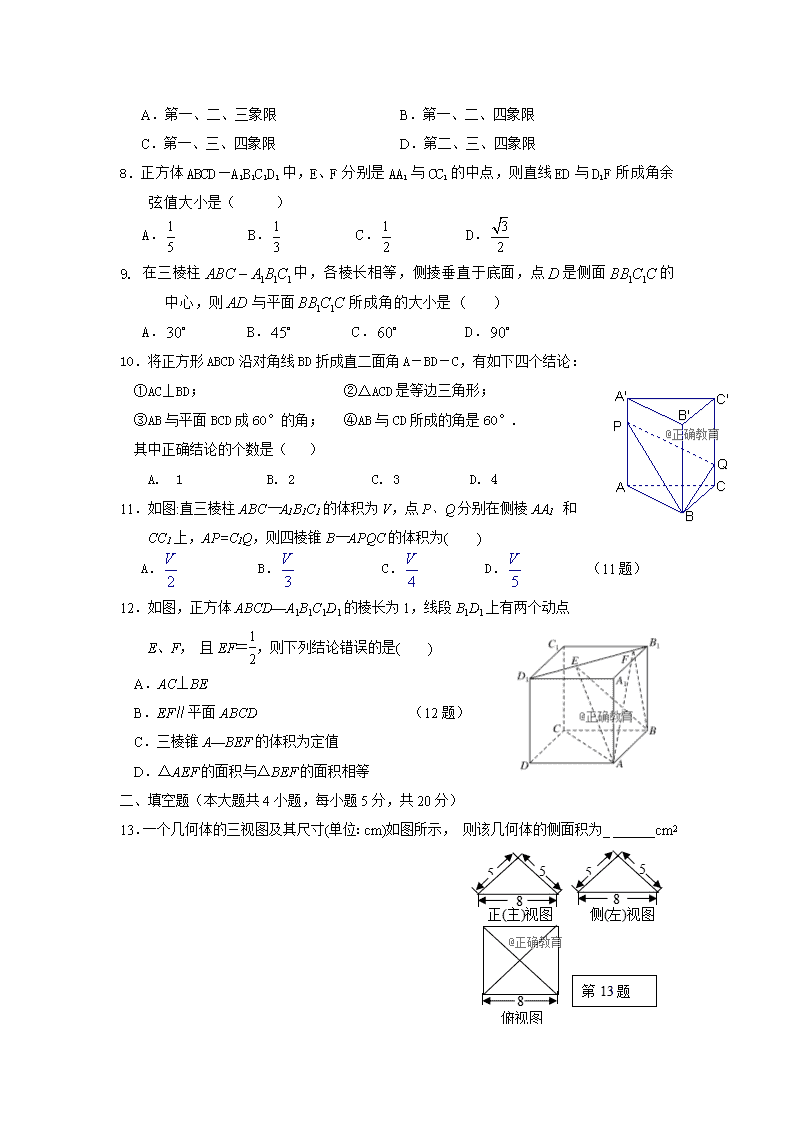
8.正方体 ABCD—A1B1C1D1 中,E、F 分别是 AA1 与 CC1 的中点,则直线 ED 与 D1F 所成角余
弦值大小是( )
A. B.
C. D.
9. 在三棱柱 中,各棱长相等,侧掕垂直于底面,点 是侧面 的
中心,则 与平面 所成角的大小是 ( )
A. B. C. D.
10.将正方形 ABCD 沿对角线 BD 折成直二面角 A-BD-C,有如下四个结论:
①AC⊥BD; ②△ACD 是等边三角形;
③AB 与平面 BCD 成 60°的角; ④AB 与 CD 所成的角是 60°.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
11.如图:直三棱柱 ABC—A1B1C1 的体积为 V,点 P、Q 分别在侧棱 AA1 和
CC1 上,AP=C1Q,则四棱锥 B—APQC 的体积为( )
A. B. C. D. (11 题)
12.如图,正方体 ABCD—A1B1C1D1 的棱长为 1,线段 B1D1 上有两个动点
E、F, 且 EF=1
2,则下列结论错误的是( )
A.AC⊥BE
B.EF∥平面 ABCD (12 题)
C.三棱锥 A—BEF 的体积为定值
D.△AEF 的面积与△BEF 的面积相等
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分)
13.一个几何体的三视图及其尺寸(单位:cm)如图所示, 则该几何体的侧面积为_ ______cm2
1
5
1
3
1
2
3
2
1 1 1ABC A B C− D 1 1BB C C
AD 1 1BB C C
30 45 60 90
2
V
3
V
4
V
5
V
14. 已知直线 与 平行,则实数 的取值
是 .
15.若直线 l 为:3y= x+6,则直线 l 的倾斜角为 .
16.球的半径为 5cm,被两个相互平行的平面所截得圆的直径分别为 6cm 和 8cm,
则这两个平面之间的距离是 cm.
三、解答题
17.(本小题 10 分)如图,在三棱柱 ABC-A1B1C1 中,△ABC 与△A1B1C1 都为正三角形且 AA1⊥
面 ABC,F、F1 分别是 AC,A1C1 的中点.
求证:(1)平面 AB1F1∥平面 C1BF;
(2)平面 AB1F1⊥平面 ACC1A1.
(17 题)
18.(本小题 12 分)设直线 l 的方程为(a+1)x+y+2-a=0 (a∈R).
(1)若 l 在两坐标轴上截距相等,求直线 l 的方程;
(2)若 l 不经过第二象限,求实数 a 的取值范围.
19.(本小题 12 分)已知直线 .
(1)若 ,求实数 的值;
(2)当 时,求直线 与 之间的距离.
1 : 2 6 0l ax y+ + = ( ) 2
2 : 1 1 0l x a y a+ − + − = a
20. (本小题 12 分)如图,DC⊥平面 ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB =
120°,
P,Q 分别为 AE,AB 的中点.
(1)证明:PQ∥平面 ACD;
(2)求 AD 与平面 ABE 所成角的正弦值
(19 题)
21.(本小题 12 分)如图所示,边长为 2 的等边△PCD 所在的平面垂直于矩形 ABCD 所在的
平面,BC=2 2,M 为 BC 的中点.
(1)证明:AM⊥PM;
(2)求二面角 P-AM-D 的大小.
(21 题)
22.如图,△ABC 中,AC=BC= AB,ABED 是边长为 1 的正方形,平面 ABED⊥底面 ABC,
若 G,F 分别是 EC,BD 的中点.
(1)求证:GF∥底面 ABC;
(2)求证:AC⊥平面 EBC; (22 题)
(3)求几何体 ADEBC 的体积 V.
2
2
理科凌志班参考答案
一、选择题:1-5 BABBD 6-10 BCACC 11-12 BD
二、填空题
13 . 80 14.-1 15 .30° 16.1 或 7
三、解答题
17 .证明:(1)在正三棱柱 ABC-A1B1C1 中,
∵F、F1 分别是 AC、A1C1 的中点,
∴B1F1∥BF,AF1∥C1F.
又∵B1F1∩AF1=F1,C1F∩BF=F,
∴平面 AB1F1∥平面 C1BF.
(2)在三棱柱 ABC-A1B1C1 中,AA1⊥平面 A1B1C1,∴B1F1⊥AA1.
又 B1F1⊥A1C1,A1C1∩AA1=A1,
∴B1F1⊥平面 ACC1A1,而 B1F1⊂平面 AB1F1,
∴平面 AB1F1⊥平面 ACC1A1.
18 .(1)3x+y=0 或 x+y+2=0;(2)a≤-1.
19.(1)由 知 ,解得 ;
(2)当 时,有 解得 ,或 a=-1(舍去)
,即 ,距离为 .
20.(1)证明:因为 P,Q 分别为 AE,AB 的中点,
所以 PQ∥EB.又 DC∥EB,因此 PQ∥DC,
又 PQ⊄平面 ACD,
从而 PQ∥平面 ACD.
(2)如图,连接 CQ,DP,因为 Q 为 AB 的中点,且 AC=BC,所以 CQ⊥AB.
因为 DC⊥平面 ABC,EB∥DC,
所以 EB⊥平面 ABC,因此 CQ⊥EB.
故 CQ⊥平面 ABE.
由(1)有 PQ∥DC,又 PQ= EB=DC,所以四边形 CQPD 为平行四边形,故 DP∥CQ,
因此 DP⊥平面 ABE,
∠DAP 为 AD 和平面 ABE 所成的角,
2
1
在 Rt△DPA 中,AD= 5,DP=1,
sin∠DAP= ,因此 AD 和平面 ABE 所成角的正弦值为
21.(1)证明:如图所示,取 CD 的中点 E,
连接 PE,EM,EA,
∵△PCD 为正三角形,
∴PE⊥CD,PE=PDsin∠PDE=2sin60°= 3.
∵平面 PCD⊥平面 ABCD,
∴PE⊥平面 ABCD,而 AM⊂平面 ABCD,∴PE⊥AM.
∵四边形 ABCD 是矩形,
∴△ADE,△ECM,△ABM 均为直角三角形,由勾股定理可求得 EM= 3,AM= 6,AE=
3,
∴EM2+AM2=AE2.∴AM⊥EM.
又 PE∩EM=E,∴AM⊥平面 PEM,∴AM⊥PM.
(2)解:由(1)可知 EM⊥AM,PM⊥AM,
∴∠PME 是二面角 P-AM-D 的平面角.
∴tan∠PME=
PE
EM=
3
3=1,∴∠PME=45°.
∴二面角 P-AM-D 的大小为 45°.
22.(1)证明:连接 AE,如下图所示.
∵ADEB 为正方形,
∴AE∩BD=F,且 F 是 AE 的中点,
又 G 是 EC 的中点,
∴GF∥AC,又 AC⊂平面 ABC,GF⊄平面 ABC,
∴GF∥平面 ABC.
(2)证明:∵ADEB 为正方形,∴EB⊥AB,
又∵平面 ABED⊥平面 ABC,平面 ABED∩平面 ABC=AB,EB⊂平面 ABED,
∴BE⊥平面 ABC,∴BE⊥AC.
又∵AC=BC=
2
2 AB,
∴CA2+CB2=AB2,
∴AC⊥BC.
又∵BC∩BE=B,∴AC⊥平面 BCE.
5
5
5
5
(3)取 AB 的中点 H,连 GH,∵BC=AC=
2
2 AB=
2
2 ,
∴CH⊥AB,且 CH=
1
2,又平面 ABED⊥平面 ABC
∴GH⊥平面 ABCD,∴V=
1
3×1×
1
2=
1
6.