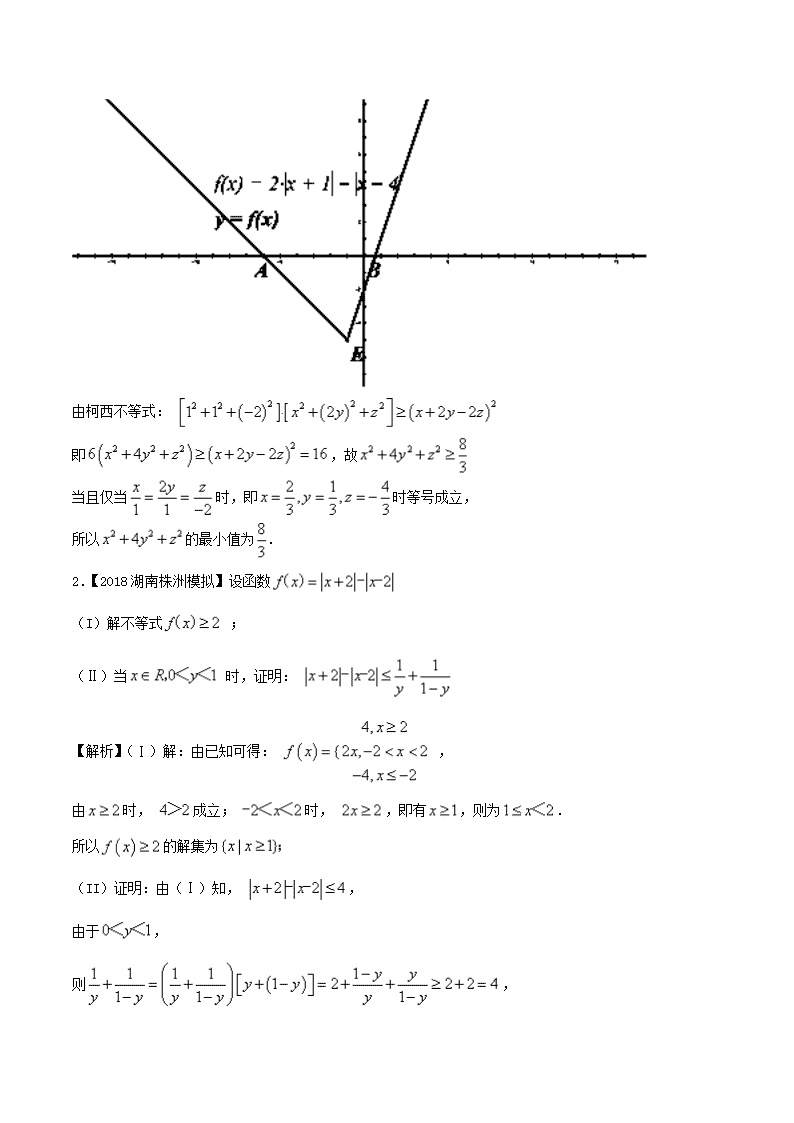专题14-4 不等式证明（文理通用）（练）-2018年高考数学一轮复习讲练测 7页

‎ ‎ ‎2018年高考数学讲练测【新课标版理】【练】选修4-5 不等式选讲 第04节 不等式证明 A基础巩固训练 ‎1. 【2018山东省实验中学第二次诊断考试】设函数 ‎（1）解不等式 ‎（2）对任意的实数，若求证： ‎ ‎2. 【2018辽宁沈阳东北育才学校二模】已知不等式的解集为.‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）若，求证： ．‎ ‎【解析】（Ⅰ）由,得 或或,‎ 解得 ‎ ‎（Ⅱ）由（Ⅰ）知 当且仅当即时取等号, ‎ ‎,即 ‎3. 【2018辽宁沈阳交联体模拟】已知 ‎（1）证明： ；‎ ‎（2）设为正数，求证： .‎ ‎【解析】 (1）‎ ‎，当且仅当时取等号， ‎ ‎(2)要证：，需证：，即证：，需证：，为正数，由基本不等式，可得 ‎，，，当且仅当时取等号，将以上三个同向不等式相乘得，即，所以原不等式成立.‎ B能力提升训练 ‎1．【2018四川成都第七中学模拟】（1）函数，若存在实数，使得成立，求实数的取值范围；‎ ‎（2）设，若，求的最小值．‎ ‎【解析】令，则，即 作出的图像，如图所示，易知其最小值为-5 ‎ 所以，实数的取值范围是 由柯西不等式： ‎ 即，故 当且仅当时，即时等号成立，‎ 所以的最小值为.‎ ‎2．【2018湖南株洲模拟】设函数 ‎ ‎（I）解不等式 ；‎ ‎（Ⅱ）当 时，证明： ‎ ‎【解析】（Ⅰ）解：由已知可得： ，‎ 由时， 成立； 时， ，即有，则为．‎ 所以的解集为 ‎ ‎（II）证明：由（Ⅰ）知， ，‎ 由于，‎ 则，‎ 则有 ‎3．设，若的解集为.‎ ‎（1）求实数的值；‎ ‎（2）若，求的最小值.‎ ‎（2）由，‎ 则，‎ 所以，此时.‎ ‎ C 思维拓展训练 ‎1．【2018黑龙江哈尔滨第六中学模拟】已知函数．‎ ‎（1）求函数的值域；‎ ‎（2）设,试比较与的大小．‎ ‎【解析】 ‎ 当时，-3<2x-7<3 ,所以． ‎ ‎（Ⅱ）由已知得．‎ 因为 ‎ 所以，故．‎ ‎ 2．【2018四川成都龙泉第二中模拟】已知函数 ‎（1）解不等式；‎ ‎（2）若，求证： .‎ ‎3．【2018四川乐山外国语学校模拟】已知函数.‎ ‎（1）解不等式；‎ ‎（2）记函数的值域为，若，证明： .‎ ‎【解析】（1）依题意，得 于是得或或 解得.‎ 即不等式的解集为.‎ ‎（2），‎ 当且仅当时，取等号，‎ ‎∴.‎ 原不等式等价于.‎ ‎∵，∴， .‎ ‎∴.‎ ‎∴.‎ ‎4.【2017课标II，理23】已知。证明：‎ ‎（1）；‎ ‎（2）。‎ ‎【解析】(1)‎ ‎(2)因为 所以，因此。‎ ‎ ‎