2019届二轮复习直线与圆课件（26张）（全国通用） 26页

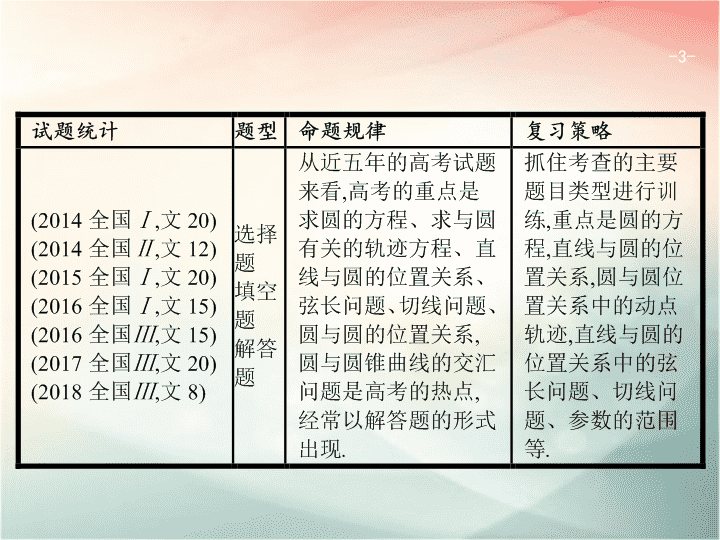
专题六　直线、圆、圆锥曲线 6.1 　直线与圆 - 3 - - 4 - 命题热点一 命题热点二 命题热点三 命题热点四 直线方程的应用 【思考】 在利用已知条件设直线方程时,应注意些什么?求直线方程的基本方法是什么 ? 例 1 若一条光线从点 ( - 2, - 3) 射出 , 经 y 轴反射后与圆 ( x+ 3) 2 + ( y- 2) 2 = 1 相切 , 则反射光线所在直线的斜率为 ( 　　 ) 答案 解析 解析 关闭 答案 解析 关闭 - 5 - 命题热点一 命题热点二 命题热点三 命题热点四 题后反思 1 . 在设直线的截距式解题时 , 要注意防止由于 “ 零截距 ” 而造成丢解的情况 . 2 . 在设直线的点斜式、斜截式解题时 , 要注意检验斜率不存在的情况 , 防止丢解 . 3 . 求直线方程的主要方法是待定系数法 . 在使用待定系数法求直线方程时 , 要注意方程的选择、分类讨论思想的应用 . - 6 - 命题热点一 命题热点二 命题热点三 命题热点四 对点训练 1 圆 x 2 +y 2 - 2 x- 8 y+ 13 = 0 的圆心到直线 ax+y- 1 = 0 的距离为 1, 则 a= ( 　　 ) A 解析 由 x 2 +y 2 - 2 x- 8 y+ 13 = 0, 得 ( x- 1) 2 + ( y- 4) 2 = 4, 所以圆心坐标为 (1,4) . 因为圆 x 2 +y 2 - 2 x- 8 y+ 13 = 0 的圆心到直线 ax+y- 1 = 0 的距离为 1, - 7 - 命题热点一 命题热点二 命题热点三 命题热点四 圆的方程及其应用 【思考】 圆的方程有几种不同形式?求圆的方程的基本方法有哪些? 例 2 设抛物线 y 2 = 4 x 的焦点为 F ,准线为 l ,已知点 C 在 l 上,以 C 为圆心的圆与 y 轴的正半轴相切于点 A ,若 ∠ FAC= 120 ° ,则圆的方程为 　　　　　　　　　　　 .   解析 抛物线 y 2 = 4 x 的焦点 F (1,0), 准线 l 的方程为 x=- 1 . 由题意可设圆 C 的方程为 ( x+ 1) 2 + ( y-b ) 2 = 1( b> 0), 则 C ( - 1, b ), A (0, b ) . ∵ ∠ FAC= 120 ° , - 8 - 命题热点一 命题热点二 命题热点三 命题热点四 题后反思 1 . 圆的三种方程 : (1) 圆的标准方程 ,( x-a ) 2 + ( y-b ) 2 =r 2 . (2) 圆的一般方程 , x 2 +y 2 +Dx+Ey+F= 0( D 2 +E 2 - 4 F> 0) . (3) 圆的直径式方程 ,( x-x 1 )( x-x 2 ) + ( y-y 1 )( y-y 2 ) = 0( 圆的直径的两端点是 A ( x 1 , y 1 ), B ( x 2 , y 2 )) . 2 . 求圆的方程一般有两类方法 : (1) 几何法 , 通过圆的性质、直线与圆、圆与圆的位置关系 , 求得 圆的基本量和方程 ; (2) 代数法 , 即用待定系数法先设出圆的方程 , 再由条件求得各系数 . - 9 - 命题热点一 命题热点二 命题热点三 命题热点四 对点训练 2 (2018 天津 , 文 12)在平面直角坐标系中,经过三点(0,0 ), ( 1,1),(2,0)的圆的方程为 　 .   答案 x 2 +y 2 - 2 x= 0 　 解析 设点 O , A , B 的坐标分别为 (0,0),(1,1),(2,0), 则 AO=AB , 所以点 A 在线段 OB 的垂直平分线上 . 又因为 OB 为该圆的一条弦 , 所以圆心在线段 OB 的垂直平分线上 , 可设圆心坐标为 (1, y ), 所以 ( y- 1) 2 = 1 +y 2 , 解得 y= 0, 所以该圆的半径为 1, 其方程为 ( x- 1) 2 +y 2 = 1, 即 x 2 +y 2 - 2 x= 0 . - 10 - 命题热点一 命题热点二 命题热点三 命题热点四 直线与圆、圆与圆的位置关系 【思考】 如何判断直线与圆、圆与圆的位置关系? 例3 (1)平行于直线2 x+y+ 1 = 0且与圆 x 2 +y 2 = 5相切的直线的方程是( 　　 ) 答案 解析 解析 关闭 答案 解析 关闭 - 11 - 命题热点一 命题热点二 命题热点三 命题热点四 答案 解析 解析 关闭 答案 解析 关闭 (2)设 A (1,0), B (0,1),直线 l : y=ax , ☉ C :( x-a ) 2 +y 2 = 1 . 若 ☉ C 既与线段 AB 有公共点,又与直线 l 有公共点,则实数 a 的取值范围是 　　　　　　　　　　 .   - 12 - 命题热点一 命题热点二 命题热点三 命题热点四 题后反思 1 . 判定直线与 圆 的 位置 关系的两种方法 : (1) 代数方法 ( 判断直线与圆方程联立所得方程组的解的情况 ), Δ> 0 ⇔ 相交 , Δ< 0 ⇔ 相离 , Δ= 0 ⇔ 相切 ; (2) 几何方法 ( 比较圆心到直线的距离与半径的大小 ), 设圆心到直线的距离为 d , 则 dr ⇔ 相离 , d=r ⇔ 相切 . 判定圆与 圆 的 位置 关系与判定直线与 圆 的 位置 关系类似 . 2 . 讨论直线与圆及圆与圆的位置关系时 , 要注意数形结合 , 充分利用圆的几何性质寻找解题途径 , 减少运算量 . - 13 - 命题热点一 命题热点二 命题热点三 命题热点四 对点训练 3 直线 l : y=kx+ 1 与圆 O : x 2 +y 2 = 1 相交于 A , B 两点 , 则 “ k= 1” 是 “ △ OAB 的面积为 ” 的 ( 　　 ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 答案 A 　 - 14 - 命题热点一 命题热点二 命题热点三 命题热点四 与圆有关的轨迹问题 【思考】 求轨迹方程常用的方法有哪些 ? 例 4 已知点 P (2,2), ☉ C : x 2 +y 2 - 8 y= 0,过点 P 的动直线 l 与 ☉ C 交于 A , B 两点,线段 AB 的中点为 M , O 为坐标原点 . (1)求 M 的轨迹方程; (2)当 |OP|=|OM| 时,求 l 的方程及 △ POM 的面积 . 解 (1) ☉ C 的方程可化为 x 2 + ( y- 4) 2 = 16, 则圆心为 C (0,4), 半径为 4 . 即 ( x- 1) 2 + ( y- 3) 2 = 2 . 因为点 P 在 ☉ C 的内部 , 所以点 M 的轨迹方程是 ( x- 1) 2 + ( y- 3) 2 = 2 . - 15 - 命题热点一 命题热点二 命题热点三 命题热点四 - 16 - 命题热点一 命题热点二 命题热点三 命题热点四 题后反思 1 . 求轨迹方程常用的方法有直接法、定义法、相关点法 ( 坐标代入法 ) 等 , 解决此类问题时要读懂题目给出的条件 , 进行合理转化 , 准确得出结论 . 2 . 涉及直线与圆的位置关系时 , 应多考虑圆的几何性质 , 利用几何法进行运算求解往往会减少运算量 . - 17 - 命题热点一 命题热点二 命题热点三 命题热点四 对点训练 4 已知过原点的动直线 l 与 ☉ C 1 : x 2 +y 2 - 6 x+ 5 = 0 相交于不同的两点 A , B. (1) 求 ☉ C 1 的圆心坐标 ; (2) 求线段 AB 的中点 M 的轨迹 C 的方程 ; (3) 是否存在实数 k , 使得直线 L : y=k ( x- 4) 与曲线 C 只有一个交点 ? 若存在 , 求出 k 的取值范围 ; 若不存在 , 说明理由 . 解 (1) ☉ C 1 : x 2 +y 2 - 6 x+ 5 = 0 可化为 ( x- 3) 2 +y 2 = 4, 所以 ☉ C 1 的圆心坐标为 (3,0) . (2) 设线段 AB 的中点 M ( x , y ), 由弦的性质可知 C 1 M ⊥ AB , 即 C 1 M ⊥ OM. 故点 M 的轨迹是以 OC 1 为直径的圆 , - 18 - 命题热点一 命题热点二 命题热点三 命题热点四 - 19 - 命题热点一 命题热点二 命题热点三 命题热点四 - 20 - 命题热点一 命题热点二 命题热点三 命题热点四 - 21 - 规律总结 拓展演练 1 . 要注意几种直线方程的局限性,点斜式、斜截式要求直线不能与 x 轴垂直,两点式要求直线不能与坐标轴垂直,而截距式方程不能表示过原点的直线,也不能表示垂直于坐标轴的直线 . 2 . 求解与两条直线平行或垂直有关的问题时,主要是利用两条直线平行或垂直的充要条件,即若斜率存在时,“斜率相等”或“互为负倒数”;若出现斜率不存在的情况,可考虑用数形结合的方法去研究 . 3 . 直线与圆的位置关系:研究直线与圆的位置关系主要通过圆心到直线的距离和半径的比较来实现,两个圆的位置关系判断依据两个圆心距离与半径差与和的比较 . 4 . 处理有关圆的问题,要特别注意圆心、半径及平面几何知识的应用,如经常用到弦心距、半径、弦长的一半构成的直角三角形,利用圆的一些特殊几何性质解题,往往使问题简化 . - 22 - 规律总结 拓展演练 1 . 已知直线 3 x+ 4 y=b 与圆 x 2 +y 2 - 2 x- 2 y+ 1 = 0 相切 , 则 b 的值是 ( 　　 ) A .- 2 或 12 B . 2 或 - 12 C .- 2 或 - 12 D . 2 或 12 D 解析 由题意 , 知圆的标准方程为 ( x- 1) 2 + ( y- 1) 2 = 1, 其圆心为 (1,1), 半径为 1, 则圆心到直线 3 x+ 4 y=b 的距离 d= = 1, 所以 b= 2 或 b= 12 . - 23 - 规律总结 拓展演练 2 . 已知点 P 在圆 x 2 +y 2 = 1上,点 A 的坐标为( - 2,0), O 为原点, 则 的 最大值为 　　　　　 .   6 - 24 - 规律总结 拓展演练 3 . 已知圆 C 的圆心在 x 轴的正半轴上,点 M (0, )在圆 C 上,且圆心到直线2 x-y= 0的距离为 ,则圆 C 的方程为 　　　　　　　　　　 . ( x- 2) 2 +y 2 = 9 - 25 - 规律总结 拓展演练 4 . 在平面直角坐标系 xOy 中 , 曲线 y=x 2 - 6 x+ 1 与坐标轴的交点都在 ☉ C 上 . (1) 求 ☉ C 的方程 ; (2) 若 ☉ C 与直线 x-y+a= 0 交于 A , B 两点 , 且 OA ⊥ OB , 求 a 的值 . - 26 - 规律总结 拓展演练