黑龙江省安达七中2020届高三数学上学期寒假考试试题2 12页

1 黑龙江省安达七中 2020 届高三数学上学期寒假考试试题（2） 一、选择题 1.已知集合  1,3,4,5,7,9U  ，  1,4,5A  ，则 U A ð （ ） A． 3,9 B． 7,9 C． 5,7,9 D． 3,7,9 2.已知 i 是虚数单位，复数 1 (2 )im m   在复平面内对应的点在第二象限，则实数 m 的取 值范围是（ ） A． , 1  B． 1,2 C． 2, D．   , 1 2,   3.某车间生产 , ,A B C 三种不同型号的产品，产量之比分别为 5 : : 3k ，为检验产品的质量,现 用分层抽样的方法抽取一个容量为 120 的样本进行检验，已知 B 种型号的产品共抽取了 24 件，则 C 种型号的产品抽取的件数为（ ） A．12 B．24 C．36 D．60 4.要得到函数 πcos(2 )4y x  的图象，只需要将函数 cosy x 的图象（ ） A．向左平行移动 π 8 个单位长度，横坐标缩短为原来的 1 2 倍，纵坐标不变. B．向左平行移动 π 4 个单位长度，横坐标缩短为原来的 1 2 倍，纵坐标不变. C．向右平行移动 π 8 个单位长度，横坐标伸长为原来的 2 倍，纵坐标不变. D．向右平行移动 π 4 个单位长度，横坐标伸长为原来的 2 倍，纵坐标不变. 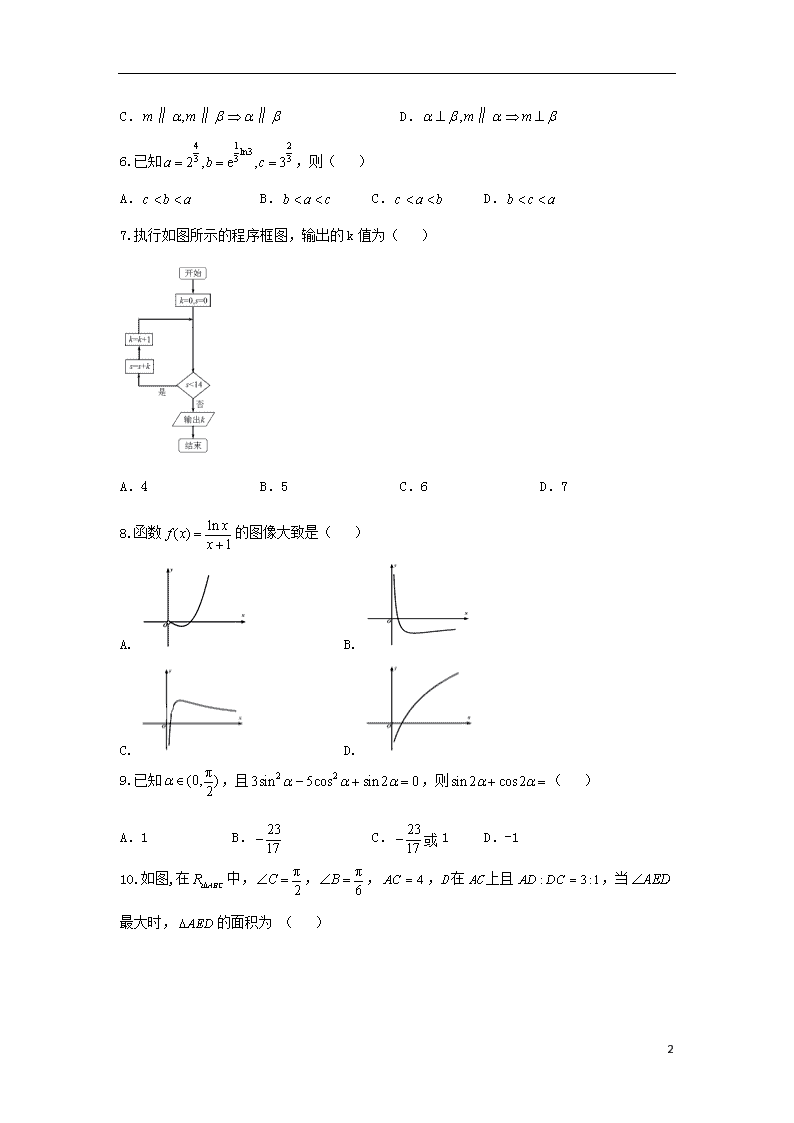5.设直线 ,m n 是两条不同的直线,  , 是两个不同的平面,下列命题中正确的是（ ） 2 A． ,m n m n ∥ ∥ ∥ B． , ,m n m n        C． ,m m   ∥ ∥ ∥ D． ,m m     ∥ 6.已知 4 1 2ln33 3 32 , e , 3a b c   ，则（ ） A． c b a  B．b a c  C． c a b  D．b c a  7.执行如图所示的程序框图，输出的 k 值为（ ） A．4 B．5 C．6 D．7 8.函数 ln( ) 1 xf x x   的图像大致是（ ） A. B. C. D. 9.已知 π(0, )2   ，且 2 23sin 5cos sin 2 0     ，则 sin 2 cos2   （ ） A．1 B． 23 17  C． 23 17  或 1 D．-1 10.如图,在 t ABCR  中， π 2C  ， π 6B  ， 4AC  ，D 在 AC 上且 : 3:1AD DC  ，当 AED 最 大时， AED 的面积为 （ ） 3 A． 3 2 B.2 C.3 D． 3 3 11.已知函数 ( ) 4 ln 3f x a x x  ，且不等式 ( 1) 4 3exf x ax ≥ ，在 (0, ) 上恒成立,则实数 a 的取值范围（ ） A． 3( , )4  B． 3( , ]4  C． ( ,0) D． ( ,0] 二、填空题 12.在等差数列{ }na 中，若 1 = 2a ， 2 3+ = 10a a ，则 7 =a __________. 13.若函数 2( ) = xf x x axe - - 在区间 0 +， 单调递增，则 a 的取值范围是_________. 14.在 ABC 中，角 A、B、C 的对边分别为 a、b、c，已知 ABC 的面积为 4， 4, 8b BA AC    ， 则 a=__________. 15.若函数 ( ) af x x ax   － 在区间  0,2 上为减函数，则满足条件的 a 的集合是________. 三、解答题 16.在 ABC 中， , ,a b c 分别为内角 , ,A B C 的对边，且满足 5cos ( )cos3a C b c A  . （1）若 1sin 5C  ， 10a c  ，求 c； （2）若 4a  ， 5c  ，求 ABC 的面积 S. 17.已知数列 na 的前 n 项和为 nS ，满足 2 2n nS a  ． （1）求数列 na 的通项公式； （2）设 (2 1)n nb n a  ,求数列 nb 的前 n 项和 nT ． 18.已知函数 3 2 21 3( ) 24 2 af x x x bx a    . （1）若 1b  ，当 0x  时， ( )f x 的图象上任意一点的切线的斜率都非负，求证： 3 3a   ； （2）若 ( )f x 在 2x   时取得极值 0，求 a b . 4 19.手机运动计步已经成为一种新时尚．某单位统计职工一天行走步数（单位：百步）得到 如下频率分布直方图： 由频率分布直方图估计该单位职工一天行走步数的中位数为 125（百步），其中同一组中的 数据用该组区间的中点值为代表． （1）试计算图中的 a、b 值，并以此估计该单位职工一天行走步数的平均值  ； （2）为鼓励职工积极参与健康步行，该单位制定甲、乙两套激励方案： 记职工个人每日步行数为 ω，其超过平均值  的百分数 ×100ω με μ -= ，若 (0,10]  ，职工获 得一次抽奖机会；若 (10,20]  ，职工获得二次抽奖机会；若 (20,30]  ，职工获得三次抽 奖机会；若 (10,20]  ，职工获得四次抽奖机会；若 超过 50，职工获得五次抽奖机会．设 职工获得抽奖次数为 n． 方案甲：从装有 1 个红球和 2 个白球的口袋中有放回的抽取 n 个小球，抽得红球个数及表示 该职工中奖几次； 方案乙：从装有 6 个红球和 4 个白球的口袋中无放回的抽取 n 个小球，抽得红球个数及表示 该职工中奖几次； 若某职工日步行数为 15700 步，试计算他参与甲、乙两种抽奖方案中奖次数的分布列．若是 你，更喜欢哪个方案？ 20.已知函数 ( ) lnf x x ax  . （1）讨论 ( )f x 在其定义域内的单调性； （2）若 1a  ，且 1 2( ) ( )f x f x ，其中 1 20 x x  ,求证： 1 2 1 2 3x x x x   . 5 21.如图所示，“8”是在极坐标系 Ox 中分别以 1 π(1, )2C 和 2 3π(2, )2C 为圆心，外切于点 O 的 两个圆.过 O 作两条夹角为 π 3 的射线分别交 1C 于 O、A 两点，交 2C 于 O、B 两点. （1）写出 1C 与 2C 的极坐标方程； （2）求 ΔOAB 面积最大值. 22.已知函数 ( ) 2 ,f x x t t   R ， ( ) 3g x x  . （1） x  R ，有 ( ) ( )f x g x ，求实数 t 的取值范围； （2）若不等式 ( ) 0f x  的解集为 1,3 ，正数 a、b 满足 2 2 2ab a b t    ，求 2a b 的最小 值. 四、证明题 23.已知向量    1, , 2, 1m  a b ，且  a b b  ，则实数 m  （ ） A．3 B． 1 2 C． 1 2  D．-3 6 参考答案 1.答案：D 解析： 2.答案：A 解析： 3.答案：C 解析：∵某工厂生产 A. B. C 三种不同型号的产品，产品数量之比依次为 5 : : 3k ， 现用分层抽样方法抽出一个容量为 120 的样本，A 种型号产品共抽取了 24 件， ∴ 24 120 5 3 k k    ，解得 2k  ， ∴C 种型号产品抽取的件数为： 24 3 362   . 4.答案：B 解析： 5.答案：B 解析： 6.答案：D 解析： 4 1 1 1 1 2 1ln3 ln33 3 3 3 3 3 32 16 , 3 , 3 9a b e e c       ∵   1 33 9 16, f x x   在 0, 上单调递增； ∴ 1 1 1 3 3 33 9 16  ∴ b c a  7.答案：C 解析： 8.答案：C 解析： 7 9.答案：A 解析：∵ 2 23sin 5cos sin 2 0     ∴ 2 23sin 5cos 2sin cos 0      ，   3sin 5cos sin cos 0      ，解得 5sin cos3    ，或 sin cos  ， ∵ π0, 2      ，∴sin cos  ，解得 π 4   ，则 π πsin 2 cos2 sin cos 12 2      10.答案：C 解析： 11.答案：B 解析： 12.答案：14 解析： 13.答案：  ,2 2ln 2  解析： 14.答案： 2 10 解析： 15.答案： 4 解析： 16.答案：（1）∵ 5cos cos3a C b c A     ∴ 5sin cos sin sin cos3A C B C A     ∴ 5sin cos cos sin sin cos3A C A C B A  ，∴  5 sin cos sin sin3 B A A C B   ∵ sin 0B  ∴ 3cos 5A  ，则 4sin 5A  ， 由正弦定理得， sin 4sin a A c C   ，即 4a c ， 联立 10a c  ，得 2c  （2）由余弦定理可得， 2 2 2 cos 2 b c aA bc   ， 8 即 2 23 5 16 ,5 6 5 55 05 2 5 b b b b      得 11 5 5b  ，则 1 22sin2 5S bc A  解析： 17.答案：（1）∵ 2 2n nS a  ，当 1n  时 1 12 2S a  ∴ 1 2a  当 2n  时 2 2n nS a  ， 1 12 2n nS a   两式相减得 12 2n n na a a   ( 2)n  12 2n na a n ， ∵ 1 2 0a   ∴ 1 2n n a a   ， 2n  ∴ na 是以首项为 2，公比为 2 的等比数列 2n na  （2）由（1）知 (2 1)2n nb n  2 3 11 2 3 2 5 2 (2 3) 2 (2 1) 2n n nT n n             2 3 4 12 1 2 3 2 5 2 (2 3) 2 (2 1) 2n n nT n n             两式相减得 2 3 12 2 2 2 2 (2 1) 2n n nT n         （ ） 3 1 1 2 1 12 (1 2 )2 (2 1) 2 2 6 (2 1) 2 (2 3)2 61 2 n n n n n nT n n n                     1(2 3)2 6n nT n    解析： 18.答案：（1） 23( ) 3 1 04f x x ax     23 1 34 x ax   3 1 34 x ax    9 ∵ 3 1 34 x x   ∴ 3 3a  ∴ 3 3a   （2） ( 2) 3 6 0f a b      2( 2) 2 6 2 2 0f a b a       解得 2 1 9 3 a a b b        或 当 1, 3a b  时 23( ) ( 2) 04f x x    ，函数无极值； ∴ 2, 9, 11a b a b    解析： 19.答案：（1） 0.012, 0.010a b  ， =125.6μ （2）某职工日行步数 = 157ω （百步）， 2× 4ε 157-126.5= 1001 .5 ≈26 ∴职工获得三次抽奖机会 设职工中奖次数为 X 在方案甲下 1(3, )3XB X 0 1 2 3 P 8 27 12 27 6 27 1 27 ( ) 1E X  10 在方案乙下 X 0 1 2 3 P 1 30 3 10 1 2 1 6 ( ) 1.8E X  所以更喜欢方案乙 解析： 20.答案：（1） 1 1( ) axf x ax x     [1]当 0a  时， ( ) 0f x  ，则 ( )f x 在区间 0,+（ ）上单调递增； [2]当 0a  时， 1(0, ), ( ) 0, ( )x f x f xa   在区间 1(0, )a 上单调递增； 1( + ), ( ) 0, ( )x f x f xa   ， 在区间 1( + )a ， 上单调递减; （2）由（1）得：当 1a  时， ( )f x 在 (0,1) 上单调递增，在 (1, ) 上单调递减， ∴ 1 20 1x x   将要证的不等式转化为 1 2 1 3 1 xx x   ＞ ，考虑到此时， 2 1x ＞ ， 1 1 3 11 x x   ＞ ， 又当 (1, )x  时， ( )f x 递增。故只需证明 1 2 1 3( ) ( )1 xf x f x   ＞ ，即证 1 1 1 3( ) ( )1 xf x f x   ＞ 设 3 3 3( ) ( ) ( ) ln ln( )1 1 1 x x xQ x f x f x xx x x           . 则 2 1 4 4 1 4 1 1( ) 1 [ ]( 1) ( 1)( 3) ( 1) 1 3 xQ x x x x x x x x x              2 2 1 4 2( 1) ( 1) ( 3) ( 1) ( 1)( 3) ( 3)( 1) x x x x x x x x x x x            . 当 (0,1)x 时， ( ) 0Q x ＜ ， ( )Q x 递减.所以，当 (0,1)x 时， ( ) (1) 0Q x Q ＞ . 11 所以 1 1 1 3( ) ( )1 xf x f x   ＞ ，从而命题得证. 解析： 21.答案：（1） 1 : 2sinC    ； 2 : 4sinC     ； （2）由（1）得 (2sin , )A   ， ( 4sin( ), )3 3B      ∴ 1 2sin [ 4sin( )]2 3ABCS        33sin(2 )6 2    3 2  解析： 22.答案：（1）由 ( ) ( )f x g x ，得 2 3x t x    恒成立 ∴ 2 3x x t    ，在 x  R 时恒成立 ∴  min2 3x x t    ∵    2 3 2 3 5x x x x        ∴ 5 2 3 5x x      ∴  min2 3 5x x     ∴ 5t   ∴t 的取值范围是  , 5  方法二：根据函数 2 3y x x    的图像，找出 2 3x x   的最小值 5 （2）由 ( ) 2 0f x x t    得 2x t  解得 2 2t x t    ∴ 2 1 2 3 t t      解得 1t  将 1t  带入 2 2 2ab a b t    ，整理得 2 0ab a b   ∴ 2 1 1b a   ∴ 2 1 2 22 ( 2 ) ( ) 5 2 4 5 9a ba b a b b a b a            当且仅当 2 2a b b a  ，即 a b 时取等号 ∴ min( 2 ) 9a b  12 解析： 23.答案：D 解析：