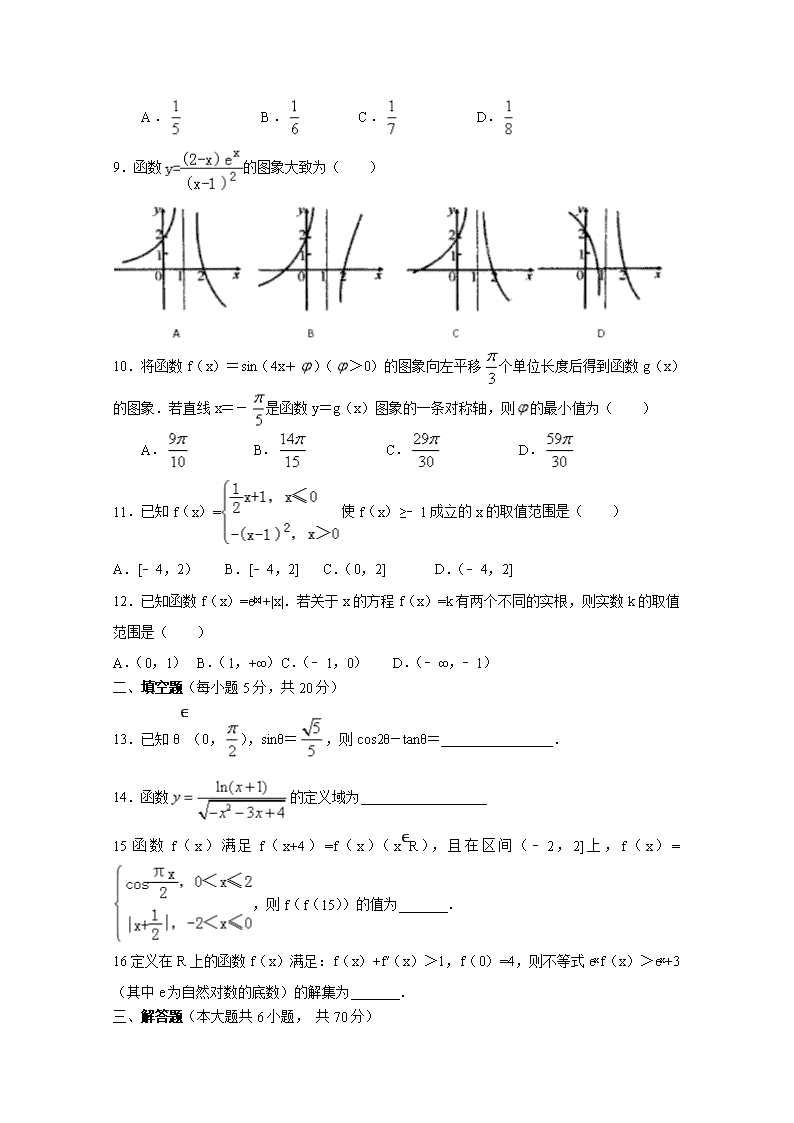- 550.00 KB
- 2021-04-19 发布
济源四中2018—2019学年上学期第一次质量检测
高三文科数学
时间:120分钟 分值:150分
命题人:苗源 做题人:席静
一、 选择题(每小题5分,共60分)
1.已知集合A={x∈Z|x-2<0},B={x|2+3x>-4},则A∩B=
A.{-1,0} B.{-1,0,1} C.{0,1} D.{-2,-1,0,1}
2.已知复数z=,则z的实部为
A.- B. C.- D.
3.如图,点O为正方形ABCD的中心,E为线段OC的中点,
则=
A.- B.-
C.+ D.+
4.已知f(x)是定义在R上的奇函数,当x>0时,f(x)=+,则f(-)=( )
A.1 B.-1 C.2 D.-2
5.已知函数f(x)=+x-2,则曲线y=f(x)在点(1,f(1))处的切线方程为( )
A.3x-4y-1=0 B.3x-4y-5=0 C.5x-4y-7=0 D.5x-4y-3=0
6.已知a=log2e,b=ln2,c=log,则a,b,c的大小关系为( )
A. a>b>c B.b>a>c C.c>b>a D.c>a>b
7.下列函数中,既是奇函数又在(0,+∞)单调递增的是( )
A. y=ex+e﹣x B.y=ln(|x|+1)C. D.
8.如图,在△ABC中,∠A=,AC=8,点D在边AB上,AD=BD,△ACD的面积 为6,则cosB=( )
A. B. C. D.
9.函数的图象大致为( )
10.将函数f(x)=sin(4x+)(>0)的图象向左平移个单位长度后得到函数g(x)的图象.若直线x=-是函数y=g(x)图象的一条对称轴,则的最小值为( )
A. B. C. D.
11.已知f(x)=使f(x)≥﹣1成立的x的取值范围是( )
A.[﹣4,2) B.[﹣4,2] C.(0,2] D.(﹣4,2]
12.已知函数f(x)=e|x|+|x|.若关于x的方程f(x)=k有两个不同的实根,则实数k的取值范围是( )
A. (0,1) B.(1,+∞) C.(﹣1,0) D.(﹣∞,﹣1)
一、 填空题(每小题5分,共20分)
13.已知θ∈(0,),sinθ=,则cos2θ-tanθ=________________.
14.函数的定义域为
15函数f(x)满足f(x+4)=f(x)(x∈R),且在区间(﹣2,2]上,f(x)=,则f(f(15))的值为 .
16定义在R上的函数f(x)满足:f(x)+f′(x)>1,f(0)=4,则不等式exf(x)>ex+3(其中e为自然对数的底数)的解集为 .
二、 解答题(本大题共6小题, 共70分)
17.(本小题满分12分)设△ABC的内角A,B,C的对边分别为a,b,c,满足
2asinA=(2sinB-sinC)b+(2sinC-sinB)c.
(1)求角A的大小;
(2)若a=2,b=2,求△ABC的面积.
18. (本小题满分12分)已知函数,曲线在点处的切线为:,若时,有极值.
(1) 求的值.
(2) 求在上的最大值和最小值.
19、(本小题满分12分)已知函数f(x)=Asin(ωx+)(A>0,ω>0,||<)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(,2)和(+2,-2).
(Ⅰ)求f(x)的解析式;
(Ⅱ)若锐角θ满足cosθ=,求f(4θ)的值。
20. (本小题满分12分)已知点是曲线上任意一点,曲线在处的切线为,求:(1)斜率最小的切线方程.(2)切线的倾斜角α的取值范围.
21.(本小题满分12分)
在直角坐标系xOy中,已知倾斜角为α的直线l经过点M(-1,0).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为+4cosθ=5.
(1)写出曲线C的直角坐标方程,并指出曲线C的形状;
(2)若直线l与曲线C有两个不同的交点A,B,且|AB|=,求α的值.
22.(本小题满分10分)
已知曲线:,直线:(为参数).
(Ⅰ)写出曲线的参数方程,直线的普通方程;(Ⅱ)若点是曲线上任意一点,求它到直线
的距离的最大值与最小值.
参考答案: