江苏省盐城中学2020届高三（尖子生班）下学期3月调研考试数学试题 Word版含解析 26页

www.ks5u.com ‎2020届高三尖子生班3月调研考试数学试题 数学（一）‎ 注意事项 考生在答题前请认真阅读本注意事项及各题答题要求．‎ ‎1．本试卷包含填空题（第1题--第14题）、解答题（第15题--第20题）．本卷满分160分 考试时间为120分钟．‎ ‎2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色签字笔填写在规定位置．‎ ‎3．请在答题卡上按顺序在对应的答题区域内作答，在其他位置作答一律无效．作答必须 用0．5毫米黑色签字笔．注意字体工整，笔记清楚．‎ ‎4．如需作图，需用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．‎ ‎5．保持答题卡卡面清洁，勿折叠、破损．一律不准用胶带纸、修正液、可擦洗的圆珠笔 一、填空题：本大题共14小题，每小题5分，计70分．请把答案写在答题卡相应位置上 ‎1.已知集合，，则________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 计算，，再计算得到答案.‎ ‎【详解】，‎ ‎，故.‎ 故答案为：.‎ ‎【点睛】本题考查了交集运算，意在考查学生的计算能力.‎ ‎2.在“一带一路”（英文：The Belt and Road，缩写B&R）知识问答竞赛中，“江苏”代表队的七名选手的比赛成绩的茎叶统计图如图所示，去掉一个最高分和一个最低分，所剩数据的方差为________．‎ - 26 -‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 剩余数据为：，计算平均值为，再计算方差得到答案.‎ ‎【详解】剩余数据为：，故，‎ 故方差为：.‎ 故答案为：.‎ ‎【点睛】本题考查了方差计算，意在考查学生的计算能力.‎ ‎3.复数z满足，为虚数单位，为复数的共轭复数，则复数的模为________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 计算到，故，再计算模长得到答案。‎ ‎【详解】，故，‎ 故，故.‎ 故答案为：.‎ ‎【点睛】本题考查了复数的计算，复数模的计算，意在考查学生的计算能力。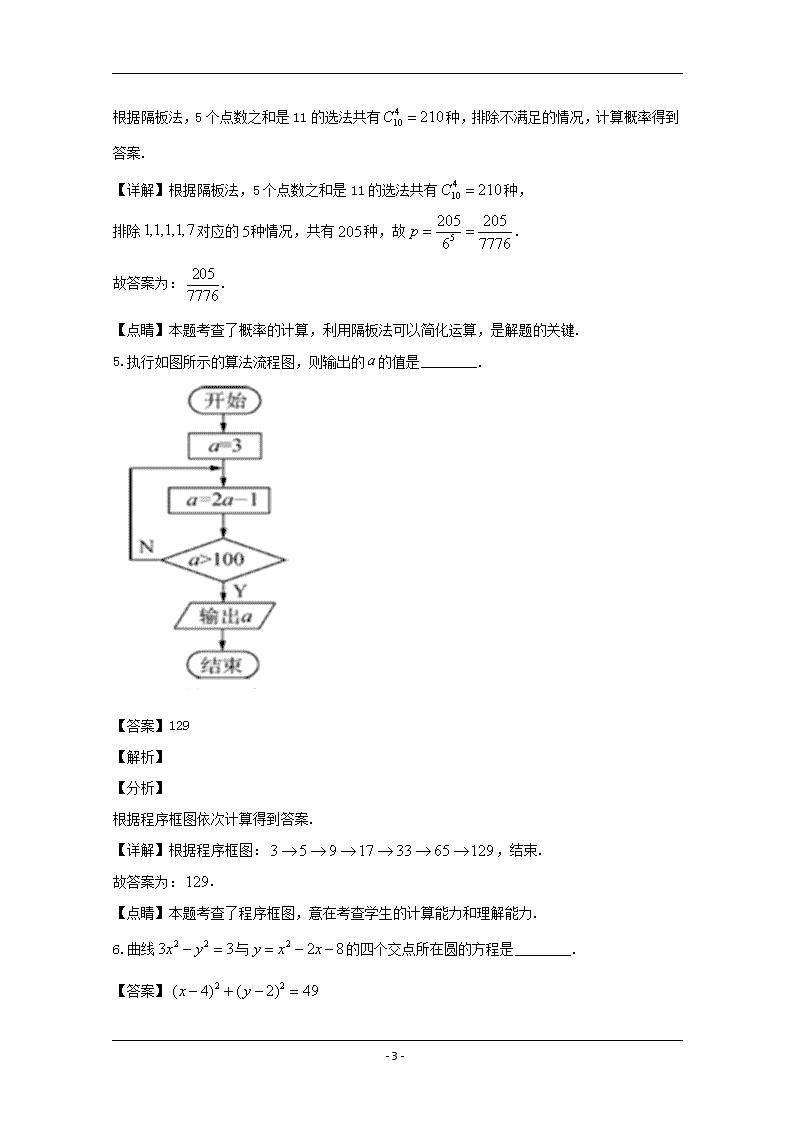‎ ‎4.随机掷出5个标准的骰子，得到5个点数之和是11的概率为________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ - 26 -‎ 根据隔板法，5个点数之和是11的选法共有种，排除不满足的情况，计算概率得到答案.‎ ‎【详解】根据隔板法，5个点数之和是11的选法共有种，‎ 排除对应的种情况，共有种，故.‎ 故答案为：.‎ ‎【点睛】本题考查了概率的计算，利用隔板法可以简化运算，是解题的关键.‎ ‎5.执行如图所示的算法流程图，则输出的的值是________．‎ ‎【答案】129‎ ‎【解析】‎ ‎【分析】‎ 根据程序框图依次计算得到答案.‎ ‎【详解】根据程序框图：，结束.‎ 故答案为：.‎ ‎【点睛】本题考查了程序框图，意在考查学生的计算能力和理解能力.‎ ‎6.曲线与的四个交点所在圆的方程是________．‎ ‎【答案】‎ - 26 -‎ ‎【解析】‎ ‎【分析】‎ 根据题意得到：，化简得到答案.‎ ‎【详解】，，故，‎ 化简整理得到：，即.‎ 故答案为：.‎ ‎【点睛】本题考查了曲线交点求圆方程，意在考查学生的计算能力和转化能力.‎ ‎7.已知，则值是_________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据角度范围得到，变换，代入数据计算得到答案.‎ ‎【详解】，故，故，‎ ‎.‎ 故答案为：.‎ ‎【点睛】本题考查了三角恒等变换求值，意在考查学生的计算能力和转化能力.‎ ‎8.在矩形中，，点在边上，点在边上．若，则的最小值是________．‎ ‎【答案】15‎ - 26 -‎ ‎【解析】‎ ‎【分析】‎ 如图所示建立直角坐标系，设，，则，根据三角函数有界性得到答案.‎ ‎【详解】如图所示建立直角坐标系，设，，‎ 则，，，‎ 即 ‎，其中，取，‎ 当时，有最小值为.‎ 故答案为：。‎ ‎【点睛】本题考查了向量的数量积的最值问题，建立坐标系可以简化运算，是解题的关键.‎ ‎9.设椭圆的左焦点为，过椭圆上一点作椭圆的切线交轴于点，若，则此椭圆的离心率为________．‎ ‎【答案】‎ - 26 -‎ ‎【解析】‎ ‎【分析】‎ 根据对称性，不妨研究椭圆的上半部分，故，计算，根据得到，代入数据计算得到答案.‎ ‎【详解】根据对称性，不妨研究椭圆的上半部分，，故，.‎ 设，故，‎ ‎，故，，化简得到.‎ ‎，则，.‎ 代入整理得到：，即.‎ 设，，故，代入化简得到：，解得.‎ 故，故.‎ 故答案为：。‎ - 26 -‎ ‎【点睛】本题考查了椭圆的离心率，意在考查学生的计算能力和综合应用能力.‎ ‎10.在正方体盒子里放入四个半径为1的球，恰好使得两个球在下方，另外两个在上方，每个球都和其他球相切，且它们都和正方体的三个面相切．则这个正方体的棱长为________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 几何体的俯视图如图1所示，如图2作辅助线，计算，得到答案.‎ ‎【详解】几何体的俯视图如图1所示，如图2作辅助线，则.‎ 故正方体的棱长为.‎ 故答案为：.‎ ‎【点睛】本题考查了正方体的内切球问题，意在考查学生的计算能力和空间想象能力.‎ - 26 -‎ ‎11.已知实数，函数在区间上的最大值是2，则______‎ ‎【答案】或 ‎【解析】‎ ‎【分析】‎ 由题意可得f（0）≤2，求得a的范围，去掉一个绝对值，再由最值的取得在顶点和端点处，计算得a的值，再检验可得a的值．‎ ‎【详解】因为函数f（x）＝|x2+|x﹣a|﹣3|在区间[﹣1，1]上的最大值是2，可得f（0）≤2，‎ 且a＞0，得|a﹣3|≤2，解得1≤a≤5，即有f（x）＝|x2﹣x+a﹣3|，﹣1≤x≤1，‎ 由f（x）的最大值在顶点或端点处取得，‎ 当f（﹣1）＝2，即|a﹣1|＝2，解得a＝3或﹣1（舍去）；‎ 当f（1）＝2，即|a﹣3|＝2，解得a＝5或a＝1；‎ 当f（）＝2，即|a﹣|＝2，解得a＝或（舍去）．‎ 当a＝1时，f（x）＝|x2﹣x﹣2|，因为f（）＝＞2，不符题意；（舍去）．‎ 当a＝5时，f（x）＝|x2﹣x+2|，因为f（-1）＝4＞2，不符题意；（舍去）．‎ 当a＝3时，f（x）＝|x2﹣x|，显然当x＝﹣1时，取得最大值2，符合题意；‎ 当a＝时，f（x）＝|x2﹣x﹣|，f（1）＝，f（﹣1）＝，f（）＝2，符合题意．‎ 故答案为3或．‎ ‎【点睛】本题考查绝对值函数的最值的求法，注意运用分类讨论思想方法，以及二次函数的图象和性质，考查运算能力，属于中档题．‎ ‎12.定义数列，先给出，接着复制该项，再添加1的后继数2，于是，接下来再复制前面所有项，之后再添加2的后继数3，如此继（1，1，2，1，1，2，3，1，1，2，1，1），设是的前项和，则__.‎ ‎【答案】3990‎ ‎【解析】‎ ‎【分析】‎ 设每操作一次形成的数列和为，的前项和为，计算得到，‎ - 26 -‎ ‎，设每操作一次形成的数列的个数为，前项和为，计算得到，，计算得到答案.‎ ‎【详解】根据题意设每操作一次形成数列和为，的前项和为，‎ 故，，，，两式相减得到.‎ 即，故是首项为，公比为的等比数列，，‎ 验证时成立，故，.‎ 设每操作一次形成的数列的个数为，其前项和为，故，，‎ 故，相减得到：，故，验证时满足.‎ ‎，，，，‎ 故 ‎.（括号内是开始的倒数个数）.‎ 故答案为：.‎ ‎【点睛】本题考查了数列前项和，意在考查学生的计算能力和应用能力.‎ ‎13.已知，分别为其左右焦点，为上任意一点，为平分线与轴交点，过作垂线，垂足分别为，求的最大值______．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 设，，，计算，化简得到，再计算最值得到答案.‎ - 26 -‎ ‎【详解】设，，，‎ 故，故，‎ ‎，‎ 故.‎ 当为上下顶点时，，，等号成立.‎ 故答案为：.‎ ‎【点睛】本题考查了椭圆内的面积的最值问题，意在考查学生的计算能力和转化能力.‎ ‎14.已知，且，则的最大值为________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 如图所示：设，，，，，，则，根据柯西不等式证明，得到，利用上面不等式得到，得到答案.‎ ‎【详解】如图所示：过作于，设，，，，，，，，.‎ 故.‎ 当，时，根据柯西不等式：，故 - 26 -‎ ‎，当时等号成立.‎ ‎，即，即.‎ 即，‎ 故，当三点共线，且，时等号成立.‎ 故答案为：.‎ ‎【点睛】本题考查了柯西不等式求最值，将表示成三角形面积是解题的关键.‎ 二、解答题：本大题共6小题，共90分．解答时需写出文字说明、证明过程或演算步骤．‎ ‎15.如图，已知四点共面，且，.‎ ‎（1）求；‎ ‎（2）求．‎ - 26 -‎ ‎【答案】（1）（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）计算，根据正弦定理计算得到答案.‎ ‎（2）根据余弦定理计算，，和差公式得到，再利用余弦定理计算得到答案.‎ ‎【详解】（1）在中，因为，所以．‎ 由正弦定理知，所以．‎ ‎（2）在中，由余弦定理知，‎ 故，解得或（舍）．‎ 由已知得是锐角，又，所以．‎ 所以 在中，由余弦定理知 ‎，解得．‎ ‎【点睛】本题考查了正弦定理，余弦定理，意在考查学生的计算能力和应用能力.‎ ‎16.如图，在多面体ABCDEF中，四边形ABCD是菱形，AC，BD相交于点O，EF∥AB，AB＝2EF，平面BCF⊥平面ABCD，BF＝CF，点G为BC的中点．求证：‎ ‎(1) 直线OG∥平面EFCD；‎ ‎(2) 直线AC⊥平面ODE.‎ - 26 -‎ ‎【答案】(1) 见解析: (2) 见解析.‎ ‎【解析】‎ 试题分析：‎ ‎(1)利用题意证得OG∥CD，结合线面平行的判断定理即可证得结论；‎ ‎(2)结合空间几何体的性质和线面垂直的判断定理即可证得题中的结论.‎ 试题解析：‎ 证明：(1) ∵ 四边形ABCD是菱形，AC∩BD＝O，‎ ‎∴ 点O是BD的中点．‎ ‎∵ 点G为BC的中点，∴ OG∥CD.‎ ‎∵ OG⊄平面EFCD，CD⊂平面EFCD，‎ ‎∴ 直线OG∥平面EFCD.‎ ‎(2) ∵ BF＝CF，点G为BC的中点，‎ ‎∴ FG⊥BC.‎ ‎∵ 平面BCF⊥平面ABCD，平面BCF∩平面ABCD＝BC，FG⊂平面BCF，FG⊥BC，‎ ‎∴ FG⊥平面ABCD.‎ ‎∵ AC⊂平面ABCD，∴ FG⊥AC.‎ ‎∵ OG∥AB，OG＝AB，EF∥AB，EF＝AB，‎ ‎∴ OG∥EF，OG＝EF，‎ ‎∴ 四边形EFGO为平行四边形，‎ ‎∴ FG∥EO.‎ ‎∴ AC⊥EO.‎ ‎∵ 四边形ABCD是菱形，∴ AC⊥DO.‎ ‎∵ EO∩DO＝O，EO，DO在平面ODE内，‎ ‎∴ AC⊥平面ODE.‎ ‎17.如图，河的两岸分别有生活小区和，其中，三点共线，与的延长线交于点，测得，，‎ - 26 -‎ ‎，，，若以所在直线分别为轴建立平面直角坐标系则河岸可看成是曲线（其中是常数）的一部分，河岸可看成是直线（其中为常数）的一部分．‎ ‎（1）求的值．‎ ‎（2）现准备建一座桥，其中分别在上，且，的横坐标为．写出桥的长关于的函数关系式，并标明定义域；当为何值时，取到最小值？最小值是多少？‎ ‎【答案】（1），.（2）；当时取到最小值，为 ‎【解析】‎ ‎【分析】‎ ‎（1）计算，，，，将点代入直线方程计算得到答案.‎ ‎（2）计算，得到，再利用均值不等式计算得到答案.‎ ‎【详解】（1）由题意得：，，∴，，，，‎ - 26 -‎ 把，代入得，解得：，‎ 把，代入得，解得.‎ ‎（2）由（1）得：点在上，∴，‎ ‎①桥的长为到直线的距离，‎ 故；‎ ‎②由①得：，‎ 而，∴，‎ 当且仅当时即“=”成立，∴.‎ ‎【点睛】本题考查了函数的应用，均值不等式求最值，意在考查学生的计算能力和应用能力.‎ ‎18.平面直角坐标系中，点是椭圆上任一点，直线截所得的弦被平分且.‎ ‎（1）判断四边形的形状；‎ ‎（2）求与的公共点数．‎ ‎【答案】（1）是平行四边形．（2）公共点数为1‎ ‎【解析】‎ ‎【分析】‎ - 26 -‎ ‎（1）联立方程得到，计算得到，根据面积得到，证明被平分，得到答案.‎ ‎（2）根据题意得到，化简得到，代入数据化简得到，得到答案.‎ ‎【详解】（1）联立直线与得，‎ 设，则．‎ ‎，，‎ 又，相减化简得，即．‎ 又，‎ 化简得：．再设，‎ 由．而，‎ 故．‎ 设0到的距离为，则，‎ 即到的距离相等，故被平分，所以是平行四边形．‎ ‎（2）由上一问知，所以，‎ 化简得，故，所以，‎ - 26 -‎ 得．显然，故与相切，公共点数为1‎ ‎【点睛】本题考查了椭圆相关四边形形状，直线和椭圆的位置关系，意在考查学生的计算能力和综合应用能力.‎ ‎19.已知函数．‎ ‎（1）若，求函数在处的切线方程；‎ ‎（2）若有两个不同的零点．‎ ‎①求的取值范围；‎ ‎②证明：当时，．‎ ‎【答案】（1）（2）①②见解析 ‎【解析】‎ ‎【分析】‎ ‎（1）求导得到，计算，，得到切线方程.‎ ‎（2）①求导得到，导函数单调递增，故存在使.故，解得或，计算得到答案.‎ ‎②构造函数，证明函数单调递增，，，代入数据计算到，，相减化简得到答案.‎ ‎【详解】（1），故，‎ 故，，故切线方程为：.‎ ‎（2）①，.‎ - 26 -‎ 易知在时单调递增，‎ 且，时，，‎ 故存在使.‎ 在上单调递减，在上单调递增，故，‎ 当时，时，，不成立；‎ 当时，时，，只需满足，‎ 即，解得或.‎ 当时，，即；‎ 当时，，即.‎ 综上所述：.‎ ‎②构造函数，故，函数单调递增，‎ ‎，故，，‎ ‎，故.‎ 故，‎ ‎，整理得到：，‎ 同理可得：，相减得到：，‎ 故.‎ ‎【点睛】本题考查了函数的切线问题，零点问题，计算量大，综合性强，意在考查学生的综合应用能力，是难题.‎ - 26 -‎ ‎20.今有一个“数列过滤器”，它会将进入的无穷非减正整数数列删去某些项，并将剩下的项按原来的位置排好形成一个新的无穷非减正整数数列，每次“过滤”会删去数列中除以余数为的项，将这样的操作记为操作.设数列是无穷非减正整数数列.‎ ‎（1）若，进行操作后得到，设前项和为 ‎①求．‎ ‎②是否存在，使得成等差？若存在，求出所有的；若不存在，说明理由．‎ ‎（2）若，对进行与操作得到，再将中下标除以4余数为0，1的项删掉最终得到证明：每个大于1的奇平方数都是中相邻两项的和．‎ ‎【答案】（1）①②不存在．见解析（2）见解析 ‎【解析】‎ ‎【分析】‎ ‎（1）计算得到，再计算得到答案，假设存在，由单调递增，不妨设，化简，不成立.‎ ‎（2）计算，根据题意得到，再证明得到答案.‎ ‎【详解】（1）①由知：当时，故．‎ 则．‎ ‎②解：假设存在，由单调递增，不妨设 化简得，显然左式为偶数，右式为奇数，矛盾，故不存在．‎ ‎（2）易知，‎ - 26 -‎ 所以保留，则．‎ 又，将删去，‎ 得到，则 也即．‎ 记，下面证明：．‎ 由，‎ 知：‎ ‎，‎ 同理可得：，‎ 合并以上四式，便证明了对任意的，都有．‎ 因此，原命题得证．‎ ‎【点睛】本题考查了数列的新定义问题，意在考查学生的对于数列知识的综合应用能力.‎ 附加题 注意事项 考生在答题前请认真阅读本注意事项及各题答题要求．‎ ‎6．本试卷包含填空题（第1题--第14题）、解答题（第15题--第20题）．本卷满分160分 考试时间为120分钟．‎ ‎7．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色签字笔填写在规定位置．‎ ‎8．请在答题卡上按顺序在对应的答题区域内作答，在其他位置作答一律无效．作答必须 用0．5毫米黑色签字笔．注意字体工整，笔记清楚．‎ ‎9．如需作图，需用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．‎ ‎10．保持答题卡卡面清洁，勿折叠、破损．一律不准用胶带纸、修正液、可擦洗的圆珠笔 ‎[选做题]（在三小题中选做2题，若多做按前两题计分，每小题10分，计20分请把答案写在答题纸的指定区域内．）‎ - 26 -‎ ‎（选修4-2：矩阵与变换）‎ ‎21.已知矩阵，向量，计算．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据，得或，得到特征向量，，故，计算得到答案.‎ ‎【详解】因，由，得或．‎ 当时，对应的一个特征向量为；‎ 当时，对应的一个特征向量为．‎ 设，解得，所以 ‎.‎ ‎【点睛】本题考查了矩阵的计算，意在考查学生的计算能力.‎ ‎（选修4-4：坐标系与参数方程）‎ ‎22.‎ 在极坐标系中，圆C的方程为，以极点为坐标原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为（t为参数），求直线l被⊙C截得的弦AB的长度．‎ ‎【答案】.‎ - 26 -‎ ‎【解析】‎ ‎【分析】‎ 先两边同乘以ρ，利用公式即可得到圆的方程，可得圆心和半径，再将直线的参数方程化为普通方程，结合直角坐标系下点到直线的距离公式求解即得．‎ ‎【详解】⊙C的方程化为ρ＝4cosθ+4sinθ，两边同乘以ρ，得ρ2＝4ρcosθ+4ρsinθ 由ρ2＝x2+y2，x＝ρcosθ，y＝ρsinθ，‎ 得x2+y2﹣4x﹣4y＝0，‎ 其圆心C坐标为（2，2），半径，‎ 又直线l的普通方程为x﹣y﹣2＝0，‎ ‎∴圆心C到直线l的距离，‎ ‎∴弦长.‎ ‎【点睛】本题考查圆的极坐标方程、参数方程与普通方程的互化，点到直线的距离公式，考查了圆中的弦长问题，属于中等题．‎ ‎（选修4-5：不等式选讲）‎ ‎23.已知为正数，且，求证．‎ ‎【答案】见解析 ‎【解析】‎ ‎【分析】‎ 直接利用均值不等式得到，再利用一次均值不等式得到答案.‎ ‎【详解】已知为正数，且，故有 ‎.当时等号成立.‎ 故．‎ ‎【点睛】本题考查了利用均值不等式证明不等式，意在考查学生的应用能力.‎ ‎[必做题]（第22、23题，每小题10分，计20分．请把答案写在答题纸的指定区域内）‎ - 26 -‎ ‎24.如图，在三棱锥P-ABC中，AC⊥BC，且，AC=BC=2，D，E分别为AB，PB中点，PD⊥平面ABC，PD=3.‎ ‎(1)求直线CE与直线PA夹角的余弦值；‎ ‎(2)求直线PC与平面DEC夹角的正弦值.‎ ‎【答案】(1)；(2).‎ ‎【解析】‎ ‎【分析】‎ ‎（1）建立空间直角坐标系，确定各点坐标，求出夹角，即可得结果；‎ ‎（2）求出平面DEC的法向量，其与法向量夹角的余弦的绝对值，即为所求角的正弦值.‎ ‎【详解】建立如图所示的空间直角坐标系，易知C(0，0，0)，‎ A(2，0，0)，D(1，1，0)，E(，，)，P(1，1，3)，‎ 设直线CE与直线PA夹角为，则 整理得；‎ 直线CE与直线PA夹角的余弦值；‎ - 26 -‎ ‎(2)设直线PC与平面DEC夹角为，‎ 设平面DEC的法向量为，‎ 因为，‎ 所以有 取，解得，，‎ 即面DEC的一个法向量为，，‎ ‎.‎ 直线PC与平面DEC夹角的正弦值为.‎ ‎【点睛】本题考查用空间向量法求空间角，注意空间角与空间向量角之间的关系，属于中档题.‎ ‎25.（1）设数列满足，用数学归纳法证明．‎ ‎（2）证明：对任意自然数，都有．‎ ‎【答案】（1）见解析（2）见解析 ‎【解析】‎ ‎【分析】‎ - 26 -‎ ‎（1）验证成立，设时，有，得到证明.‎ ‎（2）根据（1）知，迭代得到答案.‎ ‎【详解】（1）证明：显然．‎ 设时，有，‎ 则，‎ 这就是说，时也成立．‎ 于是，对任意自然数．‎ ‎（2）证明：由（1）知：，，‎ 故，即成立．‎ ‎【点睛】本题考查了数学归纳法，数列不等式证明，意在考查学生的推理能力.‎ - 26 -‎ - 26 -‎