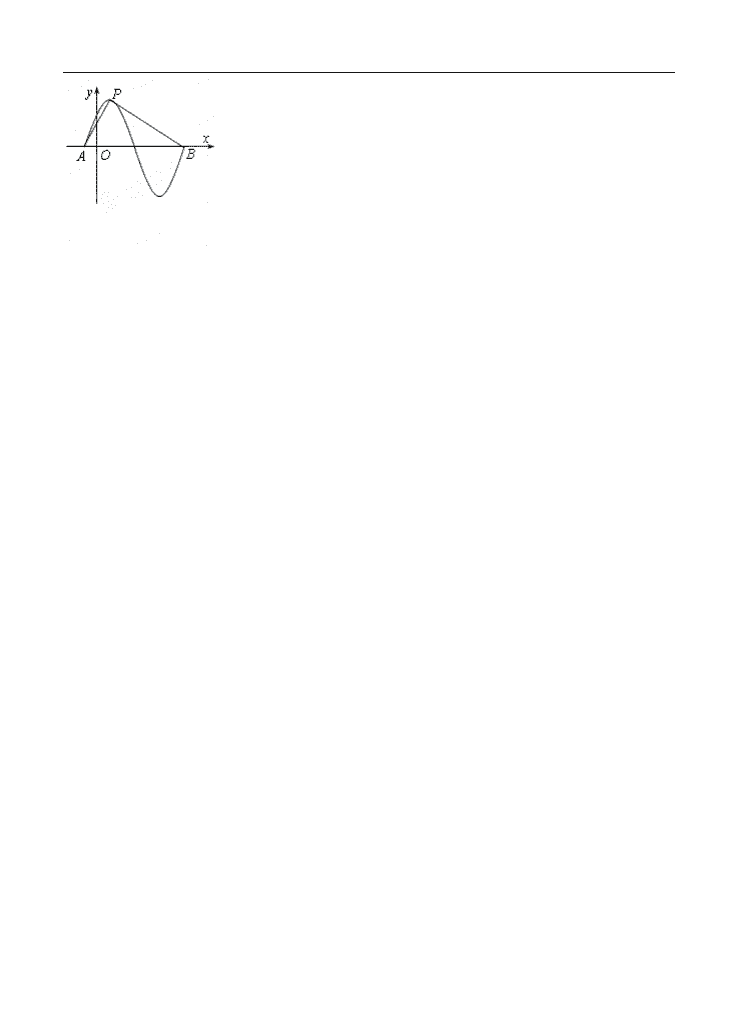- 839.00 KB
- 2021-04-19 发布
南昌市10所省重点中学命制2013届高三第二次模拟突破冲刺(二)
数学(理)试题
一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项符合题目要求的.
1.已知集合,,则( )
A. B. C. D.
2.在复平面内,复数对应的点分别为A,B.若C为线段AB的中点,则点C对应的复数的模是( )
A. B. C. D.
3.下列函数中既是偶函数,又是区间上的减函数的是( )
A. B. C. D.
4.已知函数,则=( )
A. B. C. D.
5.一个几何体的三视图如右图所示,且其左视图是一个等边三角形,则这个几何体的体积为( )
A. B.
C. D.
6.已知实数满足条件则使得目标函数
取得最大值的的值分别为( )
A.0,12 B.12,0 C.8,4 D.7,5
7.函数的部分图象如右图所示,设是图象的最高点,是图象与轴的交点,记,则的值是( )
A. B. C. D.
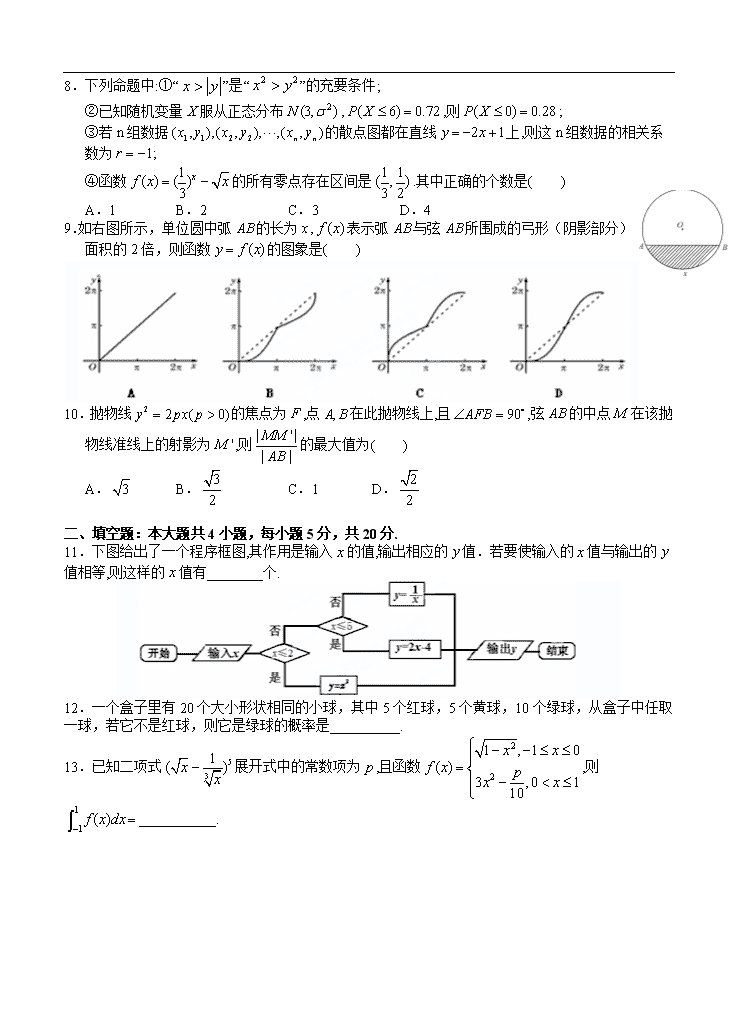
8.下列命题中:①“”是“”的充要条件;
②已知随机变量服从正态分布,,则;
③若n组数据的散点图都在直线上,则这n组数据的相关系数为;
④函数的所有零点存在区间是.其中正确的个数是( )
A.1 B.2 C.3 D.4
9.如右图所示,单位圆中弧的长为,表示弧与弦所围成的弓形(阴影部分)面积的2倍,则函数的图象是( )
10.抛物线的焦点为,点在此抛物线上,且,弦的中点在该抛物线准线上的射影为,则的最大值为( )
A. B. C.1 D.
二、填空题:本大题共4小题,每小题5分,共20分.
11.下图给出了一个程序框图,其作用是输入的值,输出相应的值.若要使输入的值与输出的值相等,则这样的值有________个.
12.一个盒子里有20个大小形状相同的小球,其中5个红球,5个黄球,10个绿球,从盒子中任取一球,若它不是红球,则它是绿球的概率是__________.
13.已知二项式展开式中的常数项为,且函数,则___________.
14.已知数列为等差数列,若,,则.类比上述结论,对于等比数列,若,则可以得到=____________.
三、选做题:请考生在下列两题中任选一题作答. 若两题都做,则按所做的第一题评阅计分,本题共5分.
15.(1)(极坐标与参数方程选做题)在极坐标系中,和极轴垂直且相交的直线l与圆相交于两点,若,则直线l的极坐标方程为____________.
(2)(不等式选做题)不等式对任意实数恒成立,则实数的取值范围是____________.
四、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
已知向量,函数
(1)求函数的最小正周期T及单调减区间;
(2)已知a,b,c分别为ABC内角A,B,C的对边,其中A为锐角,,,且.求A,b的长和ABC的面积.
17.(本小题满分12分)
小王参加一次比赛,比赛共设三关,第一、二关各有两个必答题,如果每关两个问题都答对,可进入下一关,第三关有三个问题,只要答对其中两个问题,则闯关成功.每过一关可一次性获得价值分别为1000元,3000元,6000元的奖品(不重复得奖),小王对三关中每个问题回答正确的概率依次为,且每个问题回答正确与否相互独立.
(1)求小王过第一关但未过第二关的概率;
(2)用X表示小王所获得奖品的价值,写出X的概率分布列,并求X的数学期望.
18.(本小题满分12分)
各项均为正数的数列前项和为,且.
(1)求数列的通项公式;
(2)已知公比为的等比数列满足,且存在满足,,求数列的通项公式.
19.(本小题满分12分)
如图,在正三棱柱中,,是的中点,是线段上的动点(与端点不重合),且.
(1)若,求证:;
(2)若直线与平面所成角的大小为,求的最大值.
20.(本小题满分13分)
已知椭圆的长轴长是短轴长的两倍,焦距为.
(1)求椭圆的标准方程;
(2)设不过原点的直线与椭圆交于两点、,且直线、、的斜率依次成等比数列,求△面积的取值范围.
21.(本小题满分14分)
已知函数().
(1)若函数在处取得极大值,求的值;
(2)时,函数图象上的点都在所表示的区域内,求的取值范围;
(3)证明:,.
2013届高三模拟试卷(02)数学(理)【参考答案】
二、填空题
11.3 12. 13.
14.bm+n=..解析:观察{an}的性质:am+n=,则联想nb-ma对应等比数列{bn}中的,而{an}中除以(n-m)对应等比数列中开(n-m)次方,故bm+n=.
三、选做题
15.(1). 解析:设极点为O,由该圆的极坐标方程为ρ=4,知该圆的半径为4,又直线l被该圆截得的弦长|AB|为4,所以∠AOB=60°,∴极点到直线l的距离为d=4×cos30°=2,所以该直线的极坐标方程为.
(2)或.解析:f(x)=|x+3|-|x-1|=画出函数f(x)的图象,如图,可以看出函数f(x)的最大值为4,故只要a2-3a≥4即可,解得或.
四、解答题
16.解析:(1)…………(2分)
…………………………(4分)
单调递减区间是 …………(6分)
(2); …………………………………………8分)
…………(10分). ………………………………(12分)
17.解析:(1)设小王过第一关但未过第二关的概率为P1,
则P1=2=. …………(4分)
(2)X的取值为0,1000,3000, 6000,则P(X=0)=+×=,
P(X=1000)=2=, P(X=3000)=22=,
P(X=6000)=22=,
∴X的概率分布列为
X
0
1000
3000
6000
P
…………………(10分)(错一列扣2分,扣完为止)
∴X的数学期望EX=0×+1000×+3000×+6000×=2160. ……(12分)
18.解析:(1),
两式相减得:,…………………………………(2分)
即,………………………………(4分)
为首项为1,公差为2的等差数列,故………………………(6分)
(2),依题意得,相除得……(8分)
,代入上式得q=3或q=7,…………………………………(10分)
或.…………………………………………………………………(12分)
19.解析:如图,建立空间直角系,则…(1分)
(1)当时,,此时,,…(3分)
因为,所以.………………(5分)
(2)设平面ABN的法向量,则,
即,取。而,………………(7分)………………(9分)
,,故………(11分)
当且仅当,即时,等号成立. …………………………………………(12分)
20.解析:(1)由已知得 ∴方程: (4分)
(2)由题意可设直线的方程为:
联立 消去并整理,得:
则△ ,
此时设、∴
于是 ………………(7分)
又直线、、的斜率依次成等比数列,
∴
由 得: .又由△ 得:
显然 (否则:,则中至少有一个为0,直线、 中至少有一个斜率不存在,矛盾!) ……………………………(10分)
设原点到直线的距离为,则
故由得取值范围可得△面积的取值范围为…………(13分)
21.解析:(1),由 经检验符合题意……(3分)
(2)依题意知,不等式在恒成立.令,
当k≤0时,取x=1,有,故k≤0不合.…………………………(4分)
当k>0时, g′(x)=-2kx=.
令g′(x)=0,得x1=0,x2=>-1. ……………………………(5分)
①当k≥时, ≤0,g′(x)<0在(0,+∞)上恒成立,因此g(x)在[0,+∞)上单调递减,从而对任意的x∈[0,+∞),总有g(x)≤g(0)=0,故k≥符合题意.…………(6分)
②当0<k<时,>0, 对于x∈,g′(x)>0,
故g(x)在内单调递增,因此当取x0∈时,g(x0)>g(0)=0,不合.
综上,. …………………………(8分)
(3)证明:当n=1时,不等式左边=2-ln3<2=右边,所以不等式成立.……………(9分)
当n≥2时,在(2)中取k=,得……………(10分)
取x=代入上式得:-ln(1+)≤<………(12分)
≤2-ln3+
-ln(2n+1)≤2-ln3+1-<2.
综上,-ln(2n+1)<2, ……………………………… (14分)