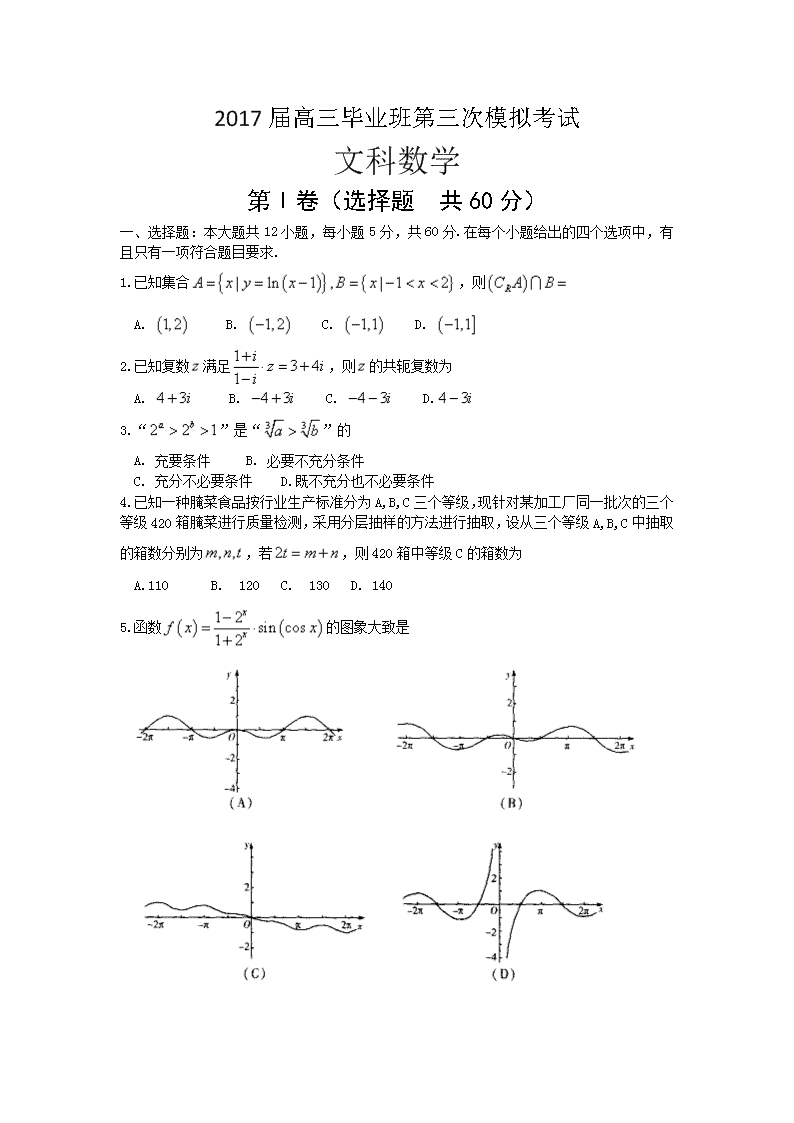
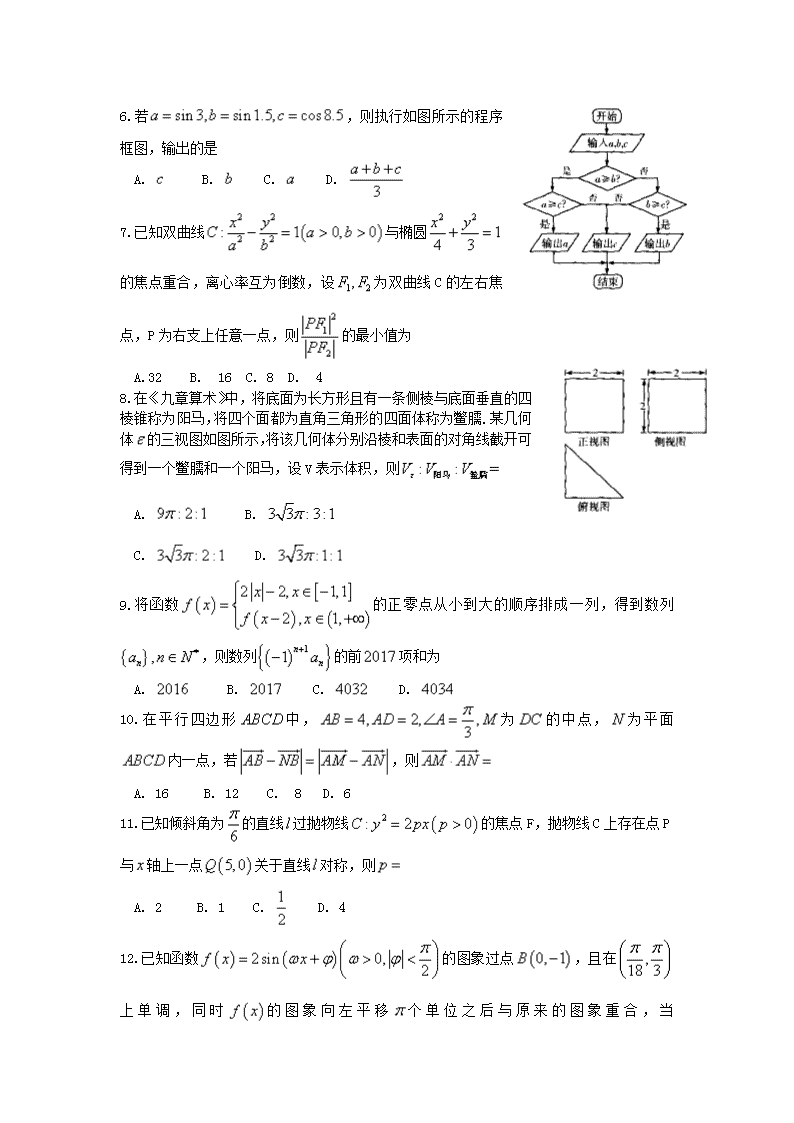
- 1.39 MB
- 2021-04-19 发布
2017届高三毕业班第三次模拟考试
文科数学
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.
1.已知集合,则
A. B. C. D.
2.已知复数满足,则的共轭复数为
A. B. C. D.
3.“”是“”的
A. 充要条件 B. 必要不充分条件
C. 充分不必要条件 D.既不充分也不必要条件
4.已知一种腌菜食品按行业生产标准分为A,B,C三个等级,现针对某加工厂同一批次的三个等级420箱腌菜进行质量检测,采用分层抽样的方法进行抽取,设从三个等级A,B,C中抽取的箱数分别为,若,则420箱中等级C的箱数为
A.110 B. 120 C. 130 D. 140
5.函数的图象大致是
6.若,则执行如图所示的程序框图,输出的是
A. B. C. D.
7.已知双曲线与椭圆的焦点重合,离心率互为倒数,设为双曲线C的左右焦点,P为右支上任意一点,则的最小值为
A.32 B. 16 C. 8 D. 4
8.在《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马,将四个面都为直角三角形的四面体称为鳖臑.某几何体的三视图如图所示,将该几何体分别沿棱和表面的对角线截开可得到一个鳖臑和一个阳马,设V表示体积,则
A. B.
C. D.
9.将函数的正零点从小到大的顺序排成一列,得到数列,则数列的前项和为
A. B. C. D.
10.在平行四边形中,为的中点,为平面内一点,若,则
A. 16 B. 12 C. 8 D. 6
11.已知倾斜角为的直线过抛物线的焦点F,抛物线C上存在点P与轴上一点关于直线对称,则
A. 2 B. 1 C. D. 4
12.已知函数的图象过点,且在上单调,同时的图象向左平移个单位之后与原来的图象重合,当
,且时,,则
A. B. C. D.
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分.
13.若函数与的图象在一个公共点处的切线相同,则实数 .
14.如图将边长为1的正六边形ABCDEF绕着直线旋转,则旋转所形成的几何体的表面积为 .
15.已知等比数列满足,且成等差数列,则的值为 .
16.已知不等式组表示的平面区域的面积为,则的取值范围为 .
三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程.
17.(本题满分12分)
已知角A,B,C为等腰的内角,设向量,且
(1)求角;
(2)在的外接圆的劣弧上取一点,使得,求及四边形的面积.
18.(本题满分12分)
某商家在网上销售一种商品,从该商品的销售数据中抽取6天的价格与销量的对应数据,如下表所示:
(1)由表中数据,看出可用线性回归模型拟合y与x的关系,试求y关于x的线性回归方程,并预测当价格为1000元时,每天的商品的销量是多少?
(2)若从这6天中随机抽取2天,求至少有1天的价格高于700元的概率.
19.(本题满分12分)
如图,在几何体中,平面,.
(1)求证:平面平面;
(2)为线段上一点,当平面时,求的值.
20.(本题满分12分)
已知椭圆的两个焦点分别为,离心率为.设过点的直线被椭圆截得的线段为,当轴时,
(1)求椭圆C的标准方程;
(2)已知点,证明:当直线变化时,总有与的斜率之积为定值.
21.(本题满分12分)
已知函数
(1)讨论的单调性;
(2)若的极值点为3,设方程的两个根为,且,
求证:.
请考生在第22、23两题中任选一题作答,如果两题都做,则按照所做的第一题给分;作答时,请用2B铅笔将答题卡上相应的题号涂黑。
22.(本题满分10分)选修4-4:参数方程与极坐标系
在平面直角坐标系中,曲线的参数方程为(为参数),在曲线上,以坐标原点O为极点,轴的正半轴为极轴的极坐标系中,两点的极坐标为
(1)求曲线的极坐标方程;
(2)设曲线的中心为,求的面积.
23.(本题满分10分)选修4-5:不等式选讲
已知函数
(1)若,求不等式的解集;
(2)当时,若的最小值为,求的最小值.