- 504.50 KB
- 2021-04-19 发布
2019 届二轮复习 选择填空标准练 (4) 作业(全国通用)
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项
是符合题目要求的)
1.已知集合 A={-1,-2,0,1},B={x|ex<1},则集合 A∩B 的元素的个数
为 ( )
A.1 B.2 C.3 D.4
【解析】选 B.A={-1,-2,0,1},B={x|ex<1}={x|x<0},所以 A∩B={-1,-2}.
2.若复数 z 满足 z(1-i)2=1+i,其中 i 为虚数单位,则 z 在复平面内所对应的点位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】选 B.z(1-i)2=1+i,所以 z= = = = =- + i,所以 z 在复平面
内所对应的点的坐标为 - , ,位于第二象限.
3.若命题“p 或 q”与命题“非 p”都是真命题,则 ( )
A.命题 p 与命题 q 都是真命题
B.命题 p 与命题 q 都是假命题
C.命题 p 是真命题,命题 q 是假命题
D.命题 p 是假命题,命题 q 是真命题
【解析】选 D.因为非 p 为真命题,所以 p 为假命题;又 p 或 q 为真命题,所以 q 为真命题.
4.在等差数列{an}中,a5=9,且 2a3=a2+6,则 a1 等于 ( )
A.-3 B.-2 C.0 D.1
【解析】选 A.根据题意,设等差数列{an}的公差为 d,首项为 a1,
若 a5=9,则有 a1+4d=9,
又由 2a3=a2+6,则 2(a1+2d)=(a1+d)+6,解得 d=3,a1=-3.
5.函数 f(x)=2 x(x<0),其值域为 D,在区间(-1,2)上随机取一个数 x,则 x∈D 的概率是
( )
A. B. C. D.
【解析】选 B.函数 f(x)=2x(x<0)的值域为(0,1),即 D=(0,1),则在区间(-1,2)上随机取一个
数 x,x∈D 的概率 P= = .
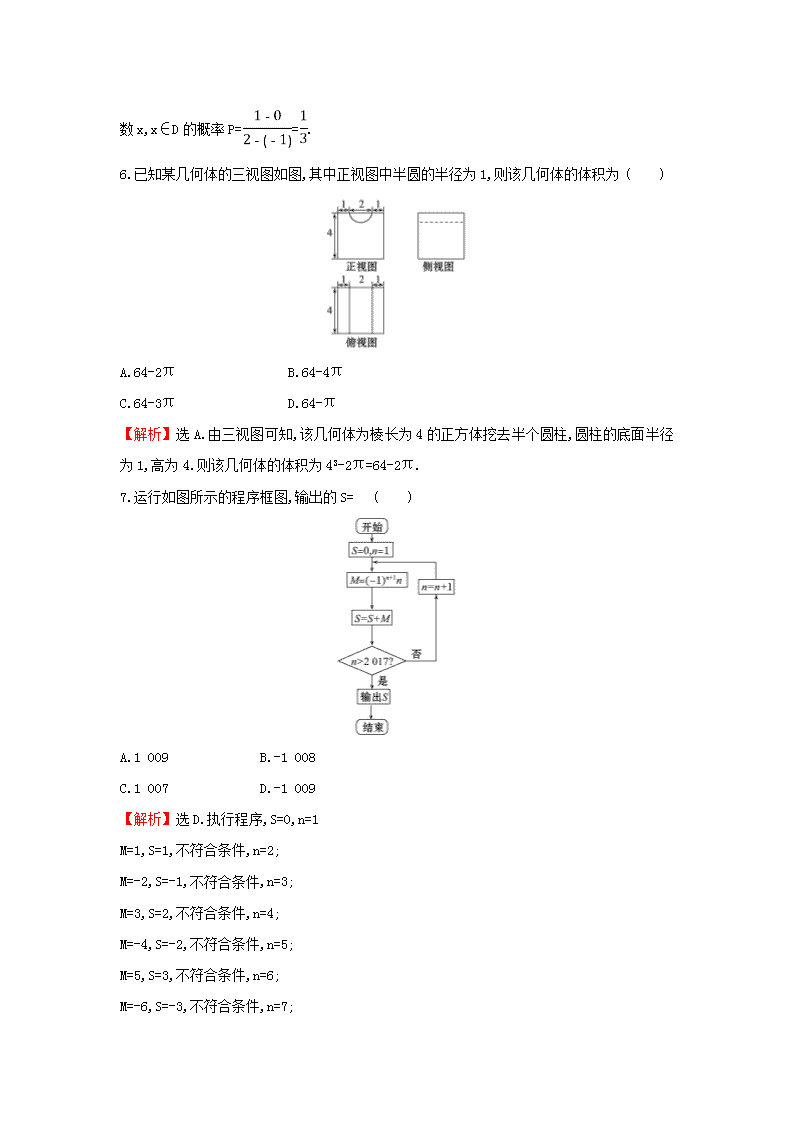
6.已知某几何体的三视图如图,其中正视图中半圆的半径为 1,则该几何体的体积为 ( )
A.64-2π B.64-4π
C.64-3π D.64-π
【解析】选 A.由三视图可知,该几何体为棱长为 4 的正方体挖去半个圆柱,圆柱的底面半径
为 1,高为 4.则该几何体的体积为 43-2π=64-2π.
7.运行如图所示的程序框图,输出的 S= ( )
A.1 009 B.-1 008
C.1 007 D.-1 009
【解析】选 D.执行程序,S=0,n=1
M=1,S=1,不符合条件,n=2;
M=-2,S=-1,不符合条件,n=3;
M=3,S=2,不符合条件,n=4;
M=-4,S=-2,不符合条件,n=5;
M=5,S=3,不符合条件,n=6;
M=-6,S=-3,不符合条件,n=7;
……
M=-2 016,S=-1 008,不符合条件,n=2 017;
M=2 017,S=1 009,不符合条件,n=2 018;
M=-2 018,S=-1 009,符合条件,输出 S=-1 009.
8.已知△ABC 中,∠A=120°,且 AB=3,AC=4,若 =λ + ,且 ⊥ ,则实数 λ 的值为
( )
A. B. C.6 D.
【解析】选 A.因为 ⊥ ,
所以 · =(λ + )·( - )=-λ + +(λ-1) · =0,
因此-λ·32+42+(λ-1)·3·4·cos 120°=0,所以λ= .
9.已知双曲线 - =1(a>0,b>0)与抛物线 y2=8x 有一个公共的焦点 F,且两曲线的一个交点
为 P,若|PF|=5,则双曲线的离心率为 ( )
A. B. C. D.2
【解析】选 D.因为抛物线 y2=8x 的焦点坐标 F(2,0),p=4,抛物线的焦点和双曲线的焦点相
同,所以 p=2c,c=2,设 P(m,n),且 n>0,由抛物线定义知:|PF|=m+ =m+2=5,所以 m=3,所以 P
点的坐标为(3,2 ),
所以 解得
又 c=2,故双曲线的离心率为 2.
10.已知实数 x,y 满足 若 z=(x-1)2+y2,则 z 的最小值
为 ( )
A.1 B. C.2 D.
【解析】选 C.绘制不等式组表示的平面区域如图所示,
目标函数的几何意义为可行域内的点与点(1,0)之间距离的平方,如图所示数形结合可得,当
目标函数过点 P(2,1)时取得最小值,zmin=(x-1)2+y2=(2-1)2+12=2.
11.在△ABC 中,内角 A,B,C 所对的边分别为 a,b,c,若 bsin 2A+
asin B=0,b= c,则 的值为 ( )
A.1 B. C. D.
【解析】选 D.由正弦定理,bsin 2A+ asin B=0,
可得 sin Bsin 2A+ sin Asin B=0,
即 2sin Bsin Acos A+ sin Asin B=0
由于 sinB sinA≠0,
所以 cos A=- ,
因为 00,b>0) 平 分 圆 x2+y2+4x-2y-1=0 的 面 积 , 则 + 的 最 小 值 为
________.
【解析】根据题意,圆心(-2,1)在直线 ax-2by+1=0 上,可得-2a-2b+1=0,即 a+b= ,
又 a>0,b>0,所以 + =2 + (a+b)
=2 3+ + ≥6+4 ,当且仅当 = 时,等号成立.
答案:6+4
16.已知数列{a n}中,对∀n∈N *,有 an+an+1+an+2=C,其中 C 为常数,若 a 5=2,a7=-3,a9=4,则
a1+a2+…+a100=________.
【解析】根据条件,可以确定该数列是以 3 为周期的周期数列,
且 a1=a7=-3,a2=a5=2,a3=a9=4,
所以 a1+a2+…+a100=33(a1+a2+a3)+a1
=33(-3+2+4)-3=96.
答案:96