- 4.46 MB
- 2021-04-19 发布
2017届临沂市高三教学质量检测考试
数学理科
2017.02
第Ⅰ卷
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1、已知为实数,为虚数单位,若,则
A. B.1 C. D.
2、已知集合,且,则集合的可能是
A. B. C. D.
3、传承传统文化在掀热潮,在刚刚过程的新春假期中,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏,下面的茎叶图是两位选手在个人追逐中的比赛得分,则下列说法正确的是
A.甲的平均数大于乙的平均数
B.甲的中位数大于乙的中位数
C.甲的方差大于乙的方差
D.甲的平均数等于乙的中位数
4、下列说法中正确的是
A.若,则 B.若命题,则为真命题
C.已知命题,“为真命题”是“为真命题”的充要条件
D.若为R上的偶函数,则
5、如图,在矩形中,分别为边、边上一点,且,现将矩形沿折起,使得平面平面,连接,则所得三棱柱的侧面面积比原来矩形的面积大约多(去)
A.
B.
C.
D.
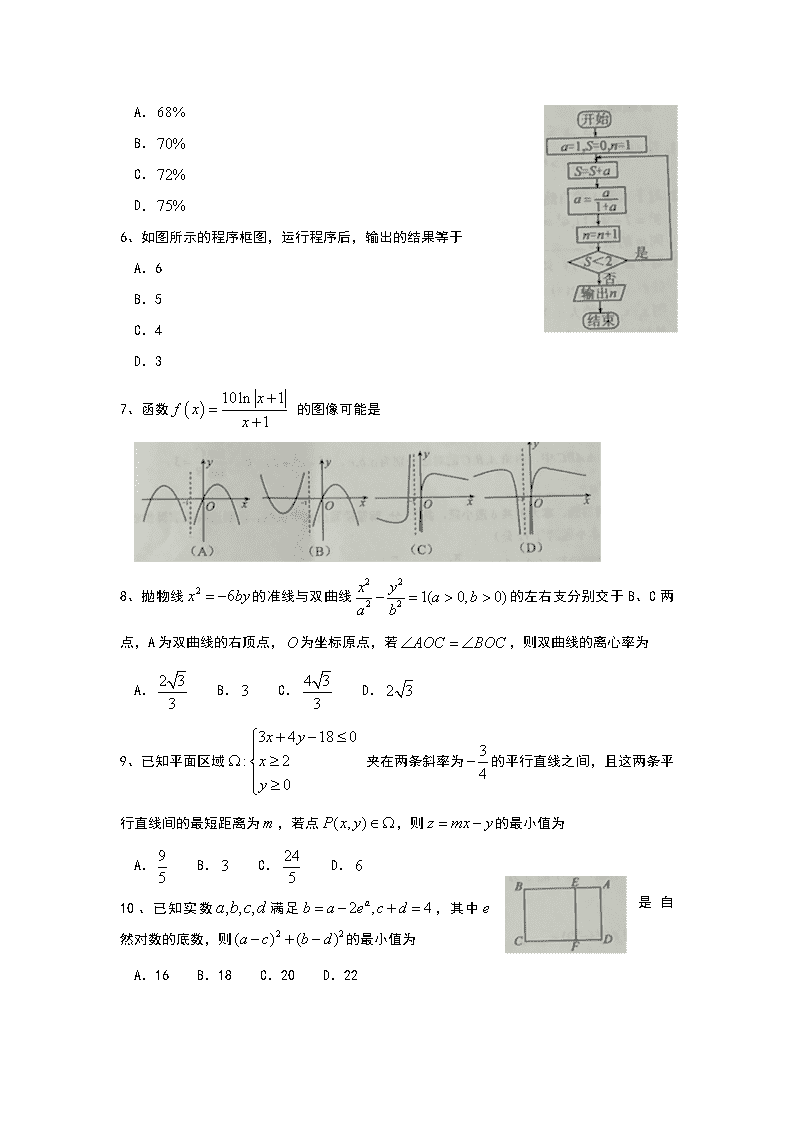
6、如图所示的程序框图,运行程序后,输出的结果等于
A.6
B.5
C.4
D.3
7、函数 的图像可能是
8、抛物线的准线与双曲线的左右支分别交于B、C两点,A为双曲线的右顶点,为坐标原点,若,则双曲线的离心率为
A. B. C. D.
9、已知平面区域 夹在两条斜率为的平行直线之间,且这两条平行直线间的最短距离为,若点,则的最小值为
A. B. C. D.
10、已知实数满足,其中是自然对数的底数,则的最小值为
A.16 B.18 C.20 D.22
第Ⅱ卷
二、填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卷的横线上..
11、若 ,则
12、对于大于1的自然数的三次幂可用奇数进行以下方式的“分裂”,
,仿此,若的“分裂数”中有一个是39,则的值为
13、对于函数,如果可导,且有实数根,则称是函数的驻点,若函数的驻点分别是,则的大小关系是 (用“ ”连接)
14、某校选定甲乙丙丁戊共5名教师去3个边远学校支教,每学校至少1人,其中甲和乙必须在同一学校,甲和丙一定在不同的学校,则不同的选派方案共有 种.
15、在中,内角的对边分别为,则
三、解答题:本大题共6小题,满分70分,解答应写出文字说明、证明过程或演算步骤
16、(本小题满分12分)
已知函数.
(1)求函数的最小周期和单调递增区间;
(2)若函数在上有两个不同的零点,求实数的取值范围,
并计算的值.
17、(本小题满分12分)
如图,正方形的对角线与相交于点,
四边形为矩形,平面平面,.
(1)求证:平面平面;
(2)若点在线段上,且,
求直线与平面所成的角的正弦值.
18、(本小题满分12分)
甲、乙两人轮流射击,每人每次射击一次,现射中者获胜,射击进行到有人获胜或每人都已射击3次时结束,设甲每次射击命中的概率为,乙每次射定击命中的概率为,且每次射击互不影响,约定由甲射击.
(1)求甲获胜的概率;
(2)求射击结束时甲的射击此时的分布列和数学期望.
19、(本小题满分12分)
已知数列的前n项和为,且 .
(1)求数列的通项公式;
(2)定义 ,其中为实数 的整数部分,为的小数部分,且,记,求数列的前n项和.
20、(本小题满分12分)
如图,椭圆的离心率为,以椭圆C的上顶点为圆心作圆: ,圆与椭圆C在第一象限交于点A,在第二象限交于点B.
(1)求椭圆C的方程;
(2)求的最小值,并求出此时圆的方程;
(3)设点P是椭圆C上异于A、B的一点,且直线分别
与轴交于 为坐标原点,求证:为定值.
21、(本小题满分14分)
已知函数
(1)讨论函数的单调性;
(2)若对于,且存在正实数,使得,
试判断与的大小关系,并给出证明.