- 532.50 KB
- 2021-04-19 发布
湖南省衡阳市第一中学2018-2019学年高二下学期期中考试
数学(文)试题
命题:彭玉锋 审核:欧小春
考试时量:120分钟 考试总分:150分
一、选择题:本大题共 12 个小题,每小题 5 分,共 60 分,在每小题给出的四个选项中, 只有一项是符合题目要求的.
1.已知集合 A={x|x-1>0},B={x|2-x<0},则下列结论正确的是
A.A∩B=A B.A∪B=B
C.“x∈A”是“x∈B”的充分条件 D.“x∈A”是“x∈B”的必要条件
2.已知复数z=,则下列结论正确的是
A.z 的虚部为i B.|z|=2 C.z2为纯虚数 D.z 的共轭复数=-1+i
3.已知,为单位向量,且⊥(+2),则向量与的夹角为
A.30° B.60° C.120° D.150°
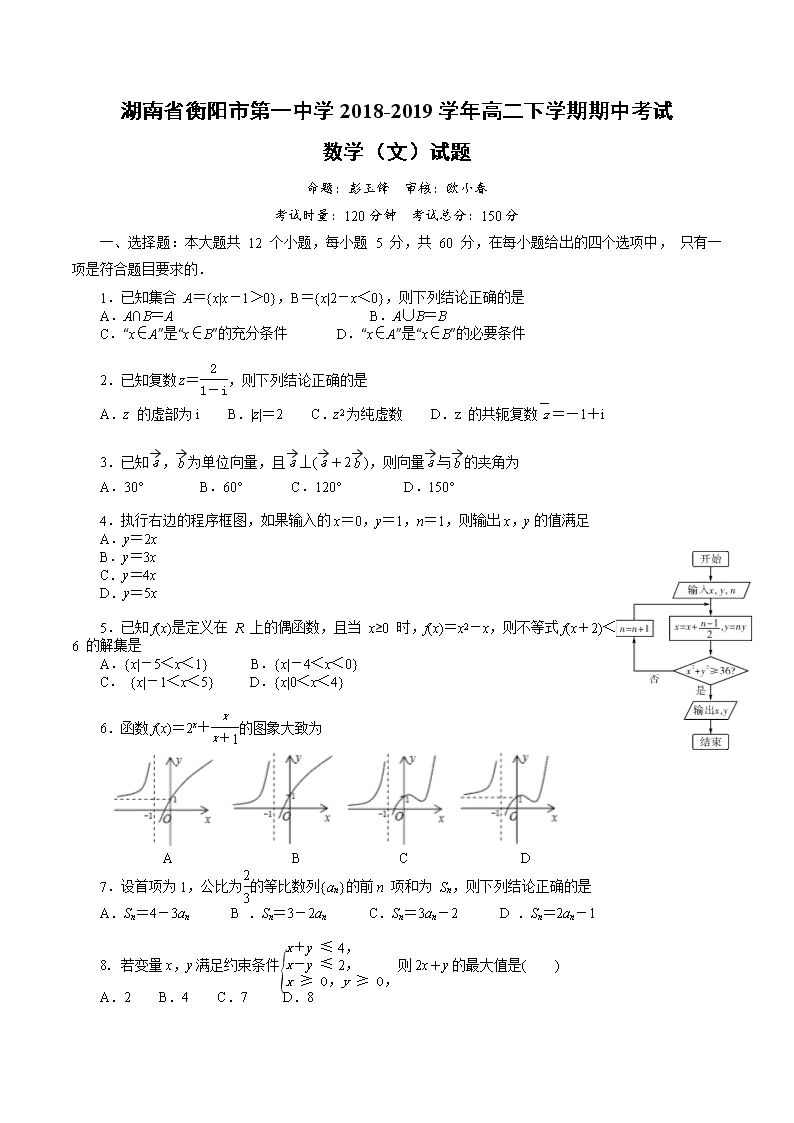
4.执行右边的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足
A.y=2x
B.y=3x
C.y=4x
D.y=5x
5.已知f(x)是定义在 R 上的偶函数,且当 x≥0 时,f(x)=x2-x,则不等式f(x+2)<6 的解集是
A.{x|-5<x<1} B.{x|-4<x<0}
C. {x|-1<x<5} D.{x|0<x<4}
6.函数f(x)=2x+的图象大致为
A B C D
7.设首项为1,公比为的等比数列{an}的前n 项和为 Sn,则下列结论正确的是
A.Sn=4-3an B .Sn=3-2an C.Sn=3an-2 D .Sn=2an-1
8.若变量x,y满足约束条件则2x+y的最大值是( )
A.2 B.4 C.7 D.8
9.若奇函数f(x)(x∈R)满足f(x+4)=,,且当x∈[0,2]时,f(x)=则f()+f()=
A. B.- C. D.
10.若两个正实数x,y满足+=1,并且x+2y>m2+2m恒成立,则实数m的取值范围是( )
A.(-∞,-2)∪[4,+∞) B.(-∞,-4]∪[2,+∞)
C.(-2,4) D.(-4,2)
11.已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|≤)的部分图象如图所示,则下列判断错误的是
A.ω=2
B.f()=1
C.函数f(x)的图象关于(-,0)对称
D.函数f(x)的图象向左平移个单位后得到y=Asinωx的图象
12.设平行于 x 轴的直线 l 分别与函数y=2x和y=2的图象相交于点 A,B,若函数y=2x的图象上存在点C,使得△ABC 为等边三角形,则这样的直线l
A.不存在 B.有且只有一条 C.至少有两条 D.有无数条
二、填空题:本大题共 4 个小题,每小题 5 分,共 20 分.把各题答案的最简形式写在题中的横线上.
13.已知函数f(x)=则f(f())=________.
14.在平面直角坐标系xOy中,直线x+2y-3=0被圆(x-2)2+(y+1)2=4截得的弦长为________.
15.在△ABC中,a=3,b=3,A=,则C=________.
16.已知函数f(x)=,若在区间[-2,2]内随机选取一个实数a,则方程[f(x)]2+a f(x)-1=0有且只有两个不同实根的概率为________.
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答.
17.(本小题满分12分)已知数列{an}是等差数列,a1=2,且a2,a3,a4+1成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=,求数列{bn}的前n项和Sn.
18.(本小题满分12分)对某班50名学生本周使用手机的时间长进行不记名问卷调查,得到的数据如下表:
时间长(小时)
[0,5)
[5,10)
[10,15)
[15,20)
[20,25)
女生人数
4
11
3
2
0
男生人数
3
17
6
3
1
(1)求这50名学生本周使用手机的平均时间长;
(2)时间长为[0,5)的7名同学中,从中抽取两名,求其中恰有一个女生的概率;
(3)若时间长为[0,10)被认定“不依赖手机”,[10,25]被认定“依赖手机”,根据以上数据完成下面的2×2列联表:
不依赖手机
依赖手机
总计
女生
男生
总计
能否在犯错概率不超过0.15的前提下,认为学生的性别与依赖手机有关系?
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:K2=,n=a+b+c+d)
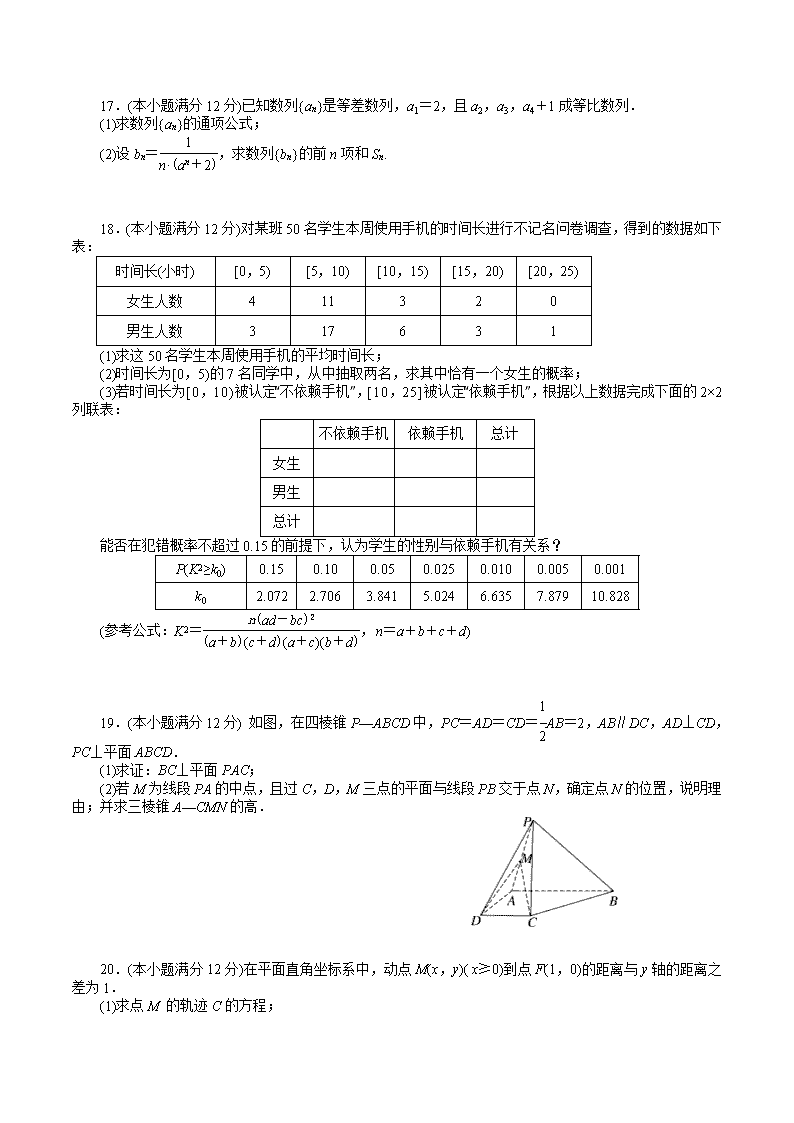
19.(本小题满分12分) 如图,在四棱锥P—ABCD中,PC=AD=CD=AB=2,AB∥DC,AD⊥CD,PC⊥平面ABCD.
(1)求证:BC⊥平面PAC;
(2)若M为线段PA的中点,且过C,D,M三点的平面与线段PB交于点N,确定点N的位置,说明理由;并求三棱锥A—CMN的高.
20.(本小题满分12分)在平面直角坐标系中,动点M(x,y)( x≥0)到点F(1,0)的距离与y轴的距离之差为1.
(1)求点M 的轨迹C的方程;
(2)若Q(-4,2),过点N(4,0)作任意一条直线交曲线C于A,B两点,试证明kQA+kQB是一个定值.
21.(本小题满分12分) 已知函数f(x)=x2ln x-a(x2-1),a∈R.
(1)当a=-1时,求曲线f(x)在点(1,f(1))处的切线方程;
(2)若当x≥1时,f(x)≥0恒成立,求a的取值范围.
请考生在第 22、23 题中任选一题作答,如果多做,则按所做的第一题计分.
22.(本小题满分10分)选修 4-4:坐标系与参数方程
以原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=4sin θ,在平面直角坐标系xOy中,直线l的方程为(t为参数).
(1)求曲线C的直角坐标方程与直线l的普通方程;
(2)已知直线l交曲线C于A,B两点,求A,B两点的距离.
23.(本小题满分 10 分)选修 4-5:不等式选讲
已知函数 f(x)=|x+2|+|x-1|.
(1)求证:f(x)≥3;
(2)求不等式f(x)≥x2的解集.