- 2.11 MB
- 2021-04-19 发布
道县、东安、江华、蓝山、宁远2020届高三12月联考试题
理科数学
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则( )
A. B. C. D.
【答案】C
【解析】
【分析】
首先确定集合中的元素,然后求交集.
【详解】由得,解得,即,
∴.
故选:C.
【点睛】本题考查集合的交集运算,掌握交集概念是解题基础.在解分式不等式时要注意分母不为0.
2.设为第三象限角,,则( )
A. B. C. D.
【答案】D
【解析】
【分析】
由同角关系求得,再由正弦的二倍角公式变形后求值.
【详解】∵设为第三象限角,,∴,
∴.
故选:D.
【点睛】本题考查同角间的三角函数关系,考查正弦的二倍角公式.在用同角间的三角函数关系求值时一定要确定角的范围,从而确定函数值的正负.
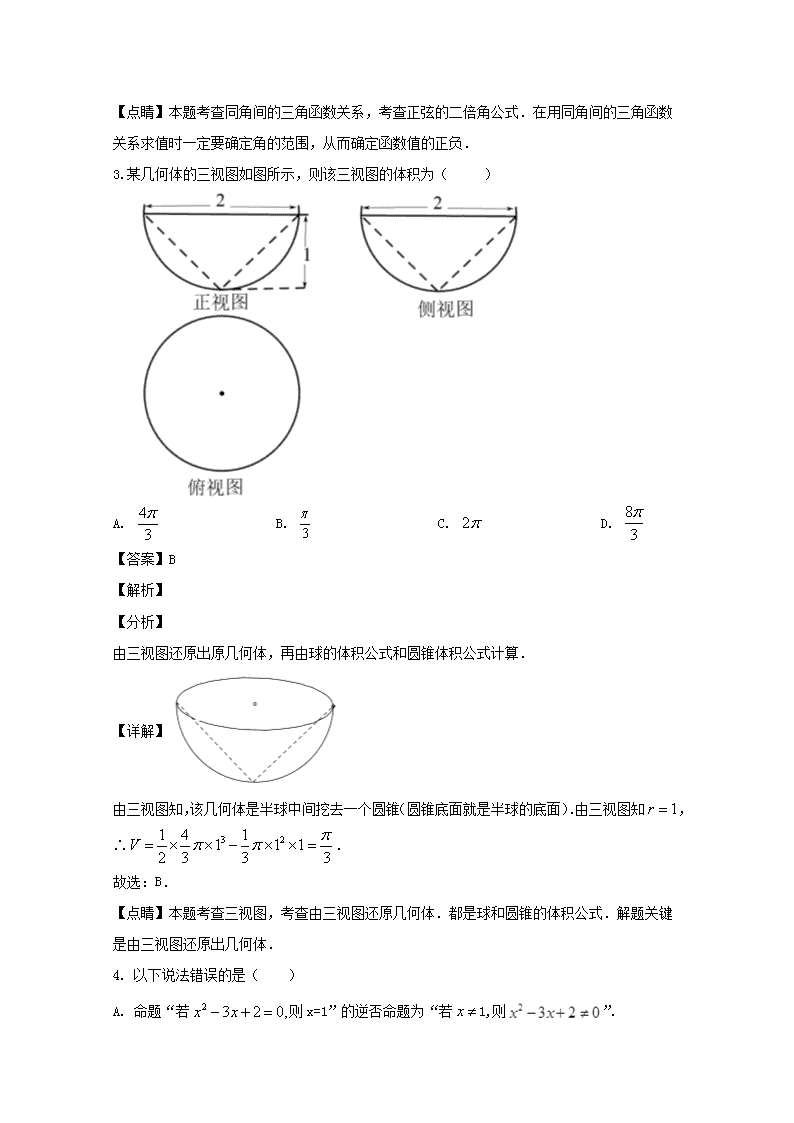
3.某几何体的三视图如图所示,则该三视图的体积为( )
A. B. C. D.
【答案】B
【解析】
【分析】
由三视图还原出原几何体,再由球的体积公式和圆锥体积公式计算.
【详解】
由三视图知,该几何体是半球中间挖去一个圆锥(圆锥底面就是半球的底面).由三视图知,∴.
故选:B.
【点睛】本题考查三视图,考查由三视图还原几何体.都是球和圆锥的体积公式.解题关键是由三视图还原出几何体.
4. 以下说法错误的是( )
A. 命题“若则x=1”的逆否命题为“若1,则”.
B. “”是“”的充分不必要条件.
C. 若为假命题,则均为假命题.
D. 若命题p:R,使得则R,则.
【答案】C
【解析】
若为假命题,则只需至少有一个为假命题即可.
5.若复数()是纯虚数,则复数在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】B
【解析】
【分析】
化简复数,由它是纯虚数,求得,从而确定对应的点的坐标.
【详解】是纯虚数,则,,
,对应点为,在第二象限.
故选:B.
【点睛】本题考查复数的除法运算,考查复数的概念与几何意义.本题属于基础题.
6.湖面上飘着一个小球,湖水结冰后将球取出,冰面上留下一个半径为,深的空穴,则取出该球前,球面上的点到冰面的最大距离为( )
A. B. C. D.
【答案】B
【解析】
试题分析:设球半径为,则,解得:
所以球面上的点到冰面的最大距离为
故选B.
考点:空间几何体的结构特征.
7.设函数,且其图像关于直线对称,则( )
A. 的最小正周期为,且在上为增函数
B. 的最小正周期为,且在上为增函数
C. 的最小正周期为,且在上为减函数
D. 的最小正周期为,且在上为减函数
【答案】C
【解析】
试题分析:,∵函数图像关于直线对称,
∴函数为偶函数,∴,∴,∴,
∵,∴,∴函数在上为减函数.
考点:1.三角函数式的化简;2.三角函数的奇偶性;3.三角函数的周期;4.三角函数的单调性.
8.若定义在R上的偶函数满足,且当时,f(x)=x,则函数y=f(x)- 的零点个数是( )
A. 6个 B. 4个 C. 3个 D. 2个
【答案】B
【解析】
因为偶函数满足,所以的周期为2,当时,,所以当时,,函数的零点等价于函数与的交点个数,在同一坐标系中,画出的图象与
的图象,如上图所示,显然的图象与的图象有4个交点.选B.
点睛:本题考查了根的存在性及根的个数判断,以及函数与方程的思想,是中档题.根据函数零点和方程的关系进行转化是解答本题的关键.
9.设,满足约束条件,则取值范围是( )
A. B. C. D.
【答案】A
【解析】
【分析】
作出可行域,,利用的几何意义求解.
【详解】作出可行域,如图内部(含边界),
,表示与可行域内点连线的斜率,
,,由图中知,∴.
故选:A.
【点睛】本题考查二元一次不等式组表示的平面区域,考查简单的非线性规划问题,解题关键是作出可行域,正确理解代数式的几何意义.
10.若函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
【答案】D
【解析】
【分析】
分段函数单调递减,要求每一段都递减的,且各段之间的函数值存在大小关系.
详解】由题意,解得.
故选:D.
【点睛】本题考查函数的单调性,分段函数在整个定义域是单调,则每一段上的单调性一致,每段顶点处的函数值也满足一定的大小关系(根据增减而定).
11.的内角,,的对边分别为,,,且,,为的外心,则( )
A. B. C. D. 6
【答案】B
【解析】
【分析】
取的中点,可得,这样,然后都用表示后运算即可.
【详解】取的中点,连接,∵是外心,∴,,
.
故选:B.
【点睛】本题考查平面向量的数量积,解题关键是取的中点,把转化为,再选取为基底,用基底进行运算.
12.已知函数,,若存在,使得,则实数的取值范围是( )
A. B. C. D.
【答案】C
【解析】
【分析】
先构造函数,再将存在性问题转化为对应函数最值问题,通过求最值得实数的取值范围.
【详解】令,则存在,使得,即的最大值,因为在上单调递减,在上单调递增,所以最大值为,因此,选C.
【点睛】利用导数解决数学问题,往往需要需要构造辅助函数.构造辅助函数常根据导数法则进行:如构造,构造,构造,构造等
二、填空题:本题共4小题,每小题5分,共20分.
13.已知等差数列,的前项和分别为,,若,则______.
【答案】
【解析】
【分析】
利用等差数列的性质可把项的比转化为前项和的比.
【详解】∵数列,都是等差数列,
∴.
故答案为:.
【点睛】本题考查等差数列的性质:等差数列中,.
由此有.
14. 观察分析下表中数据:
猜想一般凸多面体中F,V,E所满足的等式是 .
【答案】F+V﹣E=2
【解析】
试题解析:由表格可知:三棱柱:;五棱锥,,立方体,,
猜想一般凸多面体中,面数、顶点数、棱数:F、V、E所满足的等式是:.
故答案为.
考点: 欧拉定理.
15.已知函数,若使得,则实数的取值范围是________.
【答案】
【解析】
满足题意时应有:f(x)在的最小值不小于g(x)在x2∈[2,3]的最小值,
由对勾函数的性质可知函数 在区间上单调递减,
f(x)在 的最小值为f(1)=5,
当x2∈[2,3]时,g(x)=2x+a为增函数,
g(x)在x2∈[2,3]的最小值为g(2)=a+4,
据此可得:5⩾a+4,解得:a⩽1,
实数a的取值范围是(﹣∞,1],
故结果为:.
点睛:这是典型的双变元问题,首先将问题转化为在所给定义域上f(x)的最小值不小于g(x)的最小值,然后分别利用函数的单调性求得最值,最后求解不等式即可求得最终结果.本题考查了恒成立问题,对勾函数的单调性,指数函数的单调性,转化的思想等,属于常考的典型题目.
16.以双曲线:(,)的右焦点为圆心,为半径的圆与的一条渐近线交于,两点,若,则双曲线的离心率为______.
【答案】
【解析】
【分析】
求出圆心到渐近线的距离,用勾股定理表示出弦长,由弦长为可得的关系,变形后可求得离心率.
【详解】渐近线取即,圆心到它的距离为,
∴,又,∴,.
故答案为:.
【点睛】本题考查双曲线的几何性质,考查渐近线,离心率,考查直线与圆相交弦长问题.解题关键是用表示出弦长.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
17.在中,角A,B,C的对边分别是a,b,c,已知
(1)求的周长
(2)求值:的值
【答案】(1)5
(2)
【解析】
【分析】
(1)先根据余弦定理求出c,进而可求出三角形周长.
(2)根据两角差的余弦公式,需要求出角A、C的正余弦.在第(1)问的基础上,可以进一步求出角A的余弦,然后再借助同角的三角函数关系式求出A、C的正弦.问题得
【详解】解:(1) ,
所以周长为5
(2)由题可得,由正弦定理 ,解得
18.已知是由正数组成的数列,其前项和与之间满足:.
(1)求数列的通项;
(2)设,求数列的前项和.
【答案】(1); (2) .
【解析】
试题分析:(1)将原式两边平方得到 ,当时,根据 解出首项,再令 ,构造,两式相减,利用公式 ,变形为 ,所以数列是等差数列,求得通项;(2),根据错位相减法求和.
试题解析:(1)
两式相减有,化简有,
(2)
【点睛】一般数列求和的方法为:(1)分组转化法,一般适用于等差数列加等比数列,(2)裂项相消法求和,,,等的形式,(3)错位相减法求和,一般适用于等差数列乘以等比数列,(4)倒序相加法求和,一般距首末两项的和是一个常数,这样可以正着写和和倒着写和,两式两式相加除以2得到数列求和,(5)或是具有某些规律求和.
19.如图,在梯形中,,四边形为矩形,平面平面,.
(1)求证:平面;
(2)点在线段上运动,设平面与平面所成二面角为,试求的取值范围.
【答案】(1)详见解析;(2).
【解析】
【分析】
(1)由题意结合勾股定理和余弦定理可证得BC⊥AC,结合面面垂直的性质定理可得BC⊥平面ACFE.
(2)以CA,CB,CF所在的直线为x轴,y轴,z轴建立空间直角坐标系,由题意可得平面MAB的一个法向量n1=(1,,-λ),平面FCB的一个法向量n2=(1,0,0),则 cosθ=,结合三角函数的性质可得cosθ∈[,].
【详解】(1)在梯形ABCD中,∵AB∥CD,AD=DC=CB=1,∠ABC=60°,
∴AB=2,∴AC2=AB2+BC2-2AB·BC·cos 60°=3,
∴AB2=AC2+BC2,∴BC⊥AC.
又平面ACFE⊥平面ABCD,平面ACFE∩平面ABCD=AC,BC⊂平面ABCD,
∴BC⊥平面ACFE.
(2)由(1)知,可分别以CA,CB,CF所在的直线为x轴,y轴,z轴建立如图所示的空间直角坐标系,
令FM=λ(0≤λ≤),则C(0,0,0),A(,0,0),B(0,1,0),M(λ,0,1),
∴=(-,1,0),=(λ,-1,1).
设n1=(x,y,z)为平面MAB的法向量,
由,得,
取x=1,则n1=(1,,-λ)为平面MAB的一个法向量,
易知n2=(1,0,0)是平面FCB的一个法向量,
∴ cosθ= .
∵0≤λ≤, ∴当λ=0时,cosθ有最小值, 当λ=时,cosθ有最大值,∴cosθ∈[,].
【点睛】本题主要考查面面垂直的性质定理及其应用,空间直角坐标系的应用等知识,意在考查学生的转化能力和计算求解能力.
20.如图,分别过椭圆左、右焦点的动直线相交于点,与椭圆分别交于与不同四点,直线的斜率满足.已知当与轴重合时,,.
(1)求椭圆的方程;
(2)是否存在定点,使得为定值?若存在,求出点坐标并求出此定值;若不存在,说明理由.
【答案】(1);(2),和.
【解析】
试题分析:(1)当与轴重合时,垂直于轴,得,得,从而得椭圆的方程;(2)由题目分析如果存两定点,则点的轨迹是椭圆或者双曲线 ,所以把坐标化,可得点的轨迹是椭圆,从而求得定点和点.
试题解析:当与轴重合时,, 即,所以垂直于轴,得,,, 得,椭圆的方程为.
焦点坐标分别为, 当直线或斜率不存在时,点坐标为或;
当直线斜率存在时,设斜率分别为, 设由, 得:
, 所以:,, 则:
. 同理:, 因为
, 所以, 即, 由题意知, 所以
, 设,则,即,由当直线或斜率不存在时,点坐标为或也满足此方程,所以点在椭圆上.存在点和点,使得为定值,定值为.
考点:圆锥曲线的定义,性质,方程.
【方法点晴】本题是对圆锥曲线的综合应用进行考查,第一问通过两个特殊位置,得到基本量,,得,,从而得椭圆的方程,第二问由题目分析如果存两定点,则点的轨迹是椭圆或者双曲线 ,本题的关键是从这个角度出发,把坐标化,求得点的轨迹方程是椭圆,从而求得存在两定点和点.
21.已知函数:
(Ⅰ)讨论函数的单调性;
(Ⅱ)若对于任意的,,若函数在区间上有最值,求实数的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ).
【解析】
【分析】
(Ⅰ)对求导,,分,两种情况写出函数的单调区间;
(Ⅱ)对函数求导得,根据在区间上有最值,得到在区间上总不是单调函数,从而得到,另由对任意,,(a)恒成立,分离参数即可求得实数的取值范围.
【详解】解:(Ⅰ)由已知得的定义域为,且,
当时,的单调增区间为,减区间为;
当时,的单调增区间为,无减区间;
(Ⅱ),,
在区间上有最值,
在区间上总不是单调函数,
又
由题意知:对任意,,(a)恒成立,,因为,,所以,
对任意,,(3)恒成立,
【点睛】本题考查利用导数研究函数的单调性和最值问题,体现了对分类讨论和化归转化数学思想的考查,特别是问题的设置很好的考查学生对题意的理解与转化,创造性的分析问题、解决问题的能力和计算能力.
22.在平面直角坐标系中,已知曲线:(为参数),以原点为极点,轴正半轴为极轴建立极坐标系,直线:.
(1)写出直线的直角坐标方程和曲线的普通方程;
(2)在曲线上取一点,使点到直线的距离最大,求最大距离及此时点的坐标.
【答案】(1),;(2)
【解析】
【分析】
(1)由消参后可得曲线的普通方程,由可把极坐标方程化为直角坐标方程;
(2)点坐标为表示为,求出到直线距离,然后再用三角函数知识求最大值.
【详解】(1)由得曲线的普通方程为,
由得的直角坐标方程为,
(2)设,,则
当时,最大,时,,,
∴,.
【点睛】本题考查参数方程与普通方程的互化,考查极坐标方程与直角坐标方程的互化,考查点到直线的距离公式和两角差的正弦公式及正弦函数的取值.考查的知识点较多,但都是最基础的知识,本题属于中档题.
23.已知函数,.
(1)当时,求不等式的解集;
(2)若恒成立,求实数的取值范围.
【答案】(1);(2)
【解析】
【分析】
(1)按绝对值定义去绝对值符号后再解不等式;
(2)按绝对值定义去绝对值符号后得分段函数,求得其最小值,由最小值可解得范围.
【详解】(1)①当时,解得
②当时,解得
③当时,解得
∴不等式的解集为
(2)①当时,;
②当时,;
③当时,;
所以的最小值为,∴.
【点睛】本题考查含绝对值不等式的问题,含绝对值不等式可按绝对值定义去掉绝对值符号,化为分段函数,再分类求解.不等式恒成立问题可转化为求函数的最值.