- 276.00 KB
- 2021-04-19 发布
】宁晋二中2016-2017学年第一学期第二次月考(期中考试)
高二数学试题
(时间 120分钟, 满分150)
注意事项:
1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答题前,考生务必将自己的姓名、班级和准考证号填写在答题卡上..
2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再涂选其它答案标号,写在本试卷上无效.
3.回答第Ⅱ卷将答案写在答题卡上,在试题卷上作答,答案无效.
4.考试结束,只交答题卡.
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.直线x-y=0的倾斜角为( )
A.45° B.60° C.90° D.135°
2.若三点A(0,8),B(-4,0),C(m,-4)共线,则实数m的值是( )
A.6 B.-2 C.-6 D.2
3.圆x2+y2=4与圆x2+y2-6x+8y-24=0的位置关系是( )
A.相交 B.相离 C.内切 D.外切
4.如图,在长方体ABCDA1B1C1D1中,棱锥A1ABCD的体积与长方体AC1的体积的比值为( )
A. B. C. D.
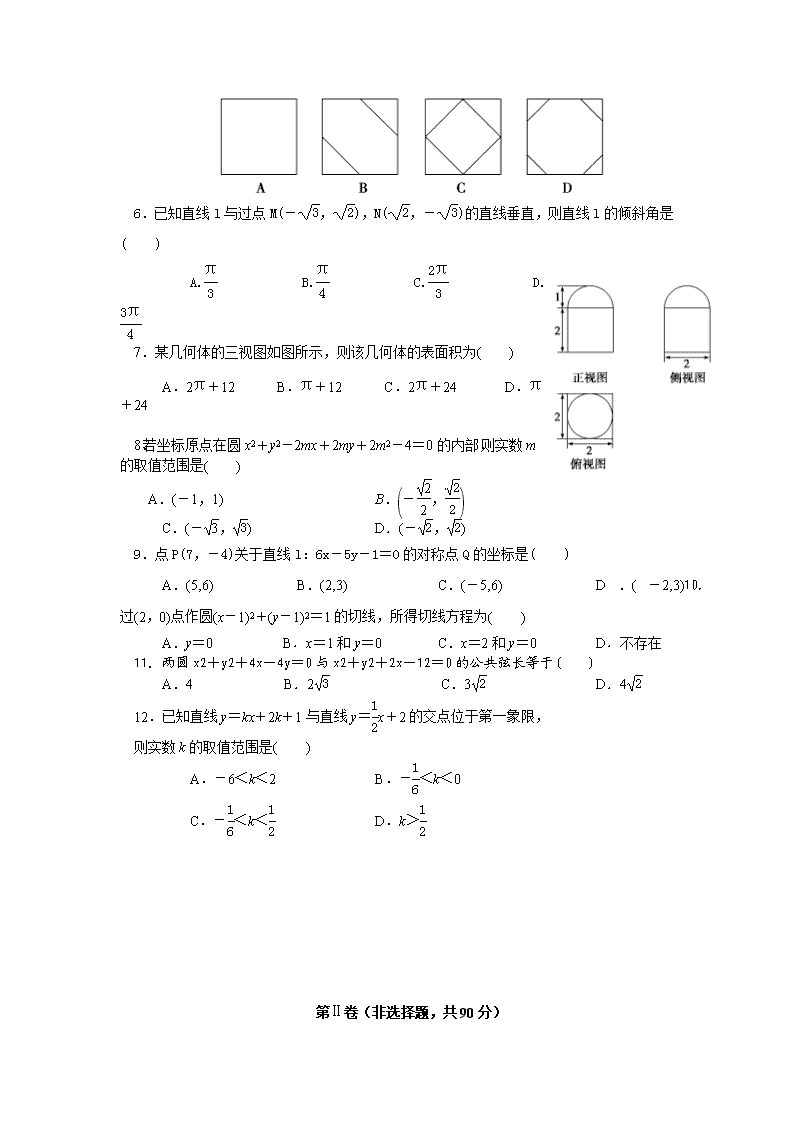
5.如图,正方体ABCDA1B1C1D1中,E,F,G,H,K,L分别为AB,BB1,B1C1,C1D1,D1D,DA的中点,则六边形EFGHKL在正方体面上的射影可能是( )
6.已知直线l与过点M(-,),N(,-)的直线垂直,则直线l的倾斜角是( )
A. B. C. D.
7.某几何体的三视图如图所示,则该几何体的表面积为( )
A.2π+12 B.π+12 C.2π+24 D.π+24
8.若坐标原点在圆x2+y2-2mx+2my+2m2-4=0的内部,则实数m的取值范围是( )
A.(-1,1) B.
C.(-,) D.(-,)
9.点P(7,-4)关于直线l:6x-5y-1=0的对称点Q的坐标是( )
A.(5,6) B.(2,3) C.(-5,6) D.(-2,3)10.过(2,0)点作圆(x-1)2+(y-1)2=1的切线,所得切线方程为( )
A.y=0 B.x=1和y=0 C.x=2和y=0 D.不存在
11.两圆x2+y2+4x-4y=0与x2+y2+2x-12=0的公共弦长等于( )
A.4 B.2 C.3 D.4
12.已知直线y=kx+2k+1与直线y=x+2的交点位于第一象限,
则实数k的取值范围是( )
A.-6<k<2 B.-<k<0
C.-<k< D.k>
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题5分,共20分。
13.在z 轴上与点A(-4,1,7)和点B(3,5,-2)等距离的点C的坐标为________.
14.若点P(1,1)为圆C:(x-3)2+y2=9的弦MN的中点,则弦MN所在直线的方程为 15.已知直线l的斜率为,且和坐标轴围成面积为3的三角形,则直线l的方程为________
16.已知点A(-1,-2),B(2,3),若直线l:x+y-c=0与线段AB有公共点,则直线l 在y 轴上的截距的取值范围
三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤。17.(本小题满分10分)
已知直线l1:ax+by+1=0(a,b不同时为0),l2:(a-2)x+y+a=0,
(1)若b=0,且l1⊥l2,求实数a的值;
(2)当b=3,且l1∥l2时,求直线l1与l2之间的距离.
18.(本小题满分12分)
如图,已知圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.
(1)求圆C的标准方程;
(2)求圆C在点B处的切线在x轴上的截距.
19.(本小题满分12分)
已知一圆经过点A(2,-3)和B(-2,-5),且圆心C在直线l:x-2y-3=0上,
(1)求此圆的标准方程;
(2)判断点M1(0,1),M2(2,-5)与该圆的位置关系.
20.(本小题满分12分)
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=,O,M分别为AB,VA的中点.
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB;
(3)求三棱锥V-ABC的体积.
21.(本小题满分12分)
已知点P(2,0)及圆C:x2+y2-6x+4y+4=0.
(1)若直线l过点P且与圆心C的距离为1,求直线l的方程.
(2)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
22.(本小题满分12分)
A,B两个工厂距一条河分别为400m和100m,A、B两工厂之间距离500m,且位于小河同侧.把小河看作一条直线,今在小河边上建一座供水站,供A,B两工厂用水,要使供水站到A,B两工厂铺设的水管长度之和最短,问供水站应建在什么地方?
数学期中考试答案
1---5 ACCCB 6----10 BDDCC 11----12 DC
13. 14 2x-y-1=0. 15. x-6y+6=0或x-6y-6=0. 16. [-3,5]
17. 解:(1)当b=0时,直线l1的方程为ax+1=0,由l1⊥l2,知a-2=0,解得a=2.
(2)当b=3时,直线l1的方程为ax+3y+1=0,当l1∥l2时,有解得a=3,
此时,直线l1的方程为3x+3y+1=0,直线l2的方程为x+y+3=0,即3x+3y+9=0.
故所求距离为d==
18解析:(1)过点C作CM⊥AB于M,连接AC,则|CM|=|OT|=1,|AM|=|AB|=1,所以圆的半径r=|AC|==,从而圆心C(1,),即圆的标准方程为(x-1)2+(y-)2=2.
(2)令x=0得,y=±1,则B(0,+1),
所以直线BC的斜率为k==-1,
由直线与圆相切的性质知,圆C在点B处的切线的斜率为1,则圆C在点B处的切线方程为y-(+1)=1×(x-0),即y=x++1,令y=0得x=--1,故所求切线在x轴上的截距为--1.
19. 解:(1)如图,因为点A(2,-3),B(-2,-5),所以线段AB的中点D的坐标为(0,-4).
又kAB==,所以线段AB的垂直平分线的方程是y=-2x-4.
联立方程组解得所以圆心坐标为C(-1,-2),半径
r=|CA|==. 所以此圆的标准方程是(x+1)2+(y+2)2=10.
(2)将点M1(0,1),M2(2,-5)分别代入(x+1)2+(y+2)2中,得值分别为10,18,
故点M1(0,1)在圆上,点M2(2,-5)在圆外.
20.
证明:(1)如图,因为O,M分别为AB,VA的中点,所以OM∥VB.
因为VB平面MOC,
所以VB∥平面MOC.
(2)因为AC=BC,O为AB的中点,所以OC⊥AB.
因为平面VAB⊥平面ABC,且OC平面ABC,
所以OC⊥平面VAB.
所以平面MOC⊥平面VAB.
(3)在等腰直角三角形ACB中,AC=BC=,所以AB=2,OC=1,所以S△VAB=,
又因为OC⊥平面VAB,所以VC-VAB=OC·S△VAB=.
因为三棱锥V-ABC的体积与三棱锥C-VAB的体积相等,所以三棱锥V-ABC的体积为
.
21. 解:(1)设直线l的斜率为k(k存在),则方程为y-0=k(x-2),即kx-y-2k=0.
又圆C的圆心为(3,-2),半径r=3,由=1,解得k=-.
所以直线方程为y=-(x-2),即3x+4y-6=0.
当l的斜率不存在时,l的方程为x=2,经验证x=2也满足条件.
(2)把直线y=ax+1代入圆C的方程,消去y,整理得(a2+1)x2+6(a-1)x+9=0.
由于直线ax-y+1=0交圆C于A,B两点,
故Δ=36(a-1)2-36(a2+1)>0,解得a<0.则实数a的取值范围是(-∞,0).
设符合条件的实数a存在.
由于l2垂直平分弦AB,故圆心C(3,-2)必在l2上.所以l2的斜率kPC=-2.
而kAB=a=-,所以a=.
由于(-∞,0),故不存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB.
22.
如图,以小河所在直线为x轴,过点A的垂线为y轴,建立直角坐标系,
则点A(0,400),点B(a,100).
过点B作BC⊥AO于点C.
在△ABC中,AB=500,AC=400-100=300,
由勾股定理得BC=400,所以B(400,100).
点A(0,400)关于x轴的对称点A′(0,-400),由两点式得直线A′B的方程为y=x-400.
令y=0,得x=320,即点P(320,0).
故供水站(点P)在距O点320 m处时,到A,B两厂铺设的水管长度之和最短.o