- 783.00 KB
- 2021-04-19 发布
甘谷一中2017——2018学年高三第一次检测考试
数学(文)
第I卷(选择题 共60分)
一、选择题
(本大题共12个小题,每小题5分,共计60分,在每小题题给出的四个选项中,只有一项符合题目要求)【来源:全,品…中&高*考+网】
1.已知集合, ,若,则为( )
A. B. C. D. 【来源:全,品…中&高*考+网】
2., ,则( )
A. B. C. D.
3.下列函数中,既不是奇函数,也不是偶函数的是( )
A. B. C. D.
4.王安石在《游褒禅山记》中写道“世之奇伟、瑰怪,非常之观,常在于险远,而人之所罕至焉,故非有志者不能至也”,请问“有志”是到达“奇伟、瑰怪,非常之观”的 ( )
A. 充要条件 B. 既不充分也不必要条件 C. 充分不必要条件 D. 必要不充分条件
5.有下列四个命题:
①“若,则互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若,则有实根”的逆否命题;
④“不等边三角形的三个内角相等”逆命题;
其中真命题为( )
A. ①② B. ②③ C. ①③ D. ③④
6.已知函数的定义域是,值域为,则的取值范围是( )
A. B. C. D.
7.函数的零点个数为( )
A. 3 B. 2 C. 1 D. 0
8.已知是定义在R上的偶函数,且在区间上单调递增。若实数满足,则的取值范围是 ( )
A. B. C. D.
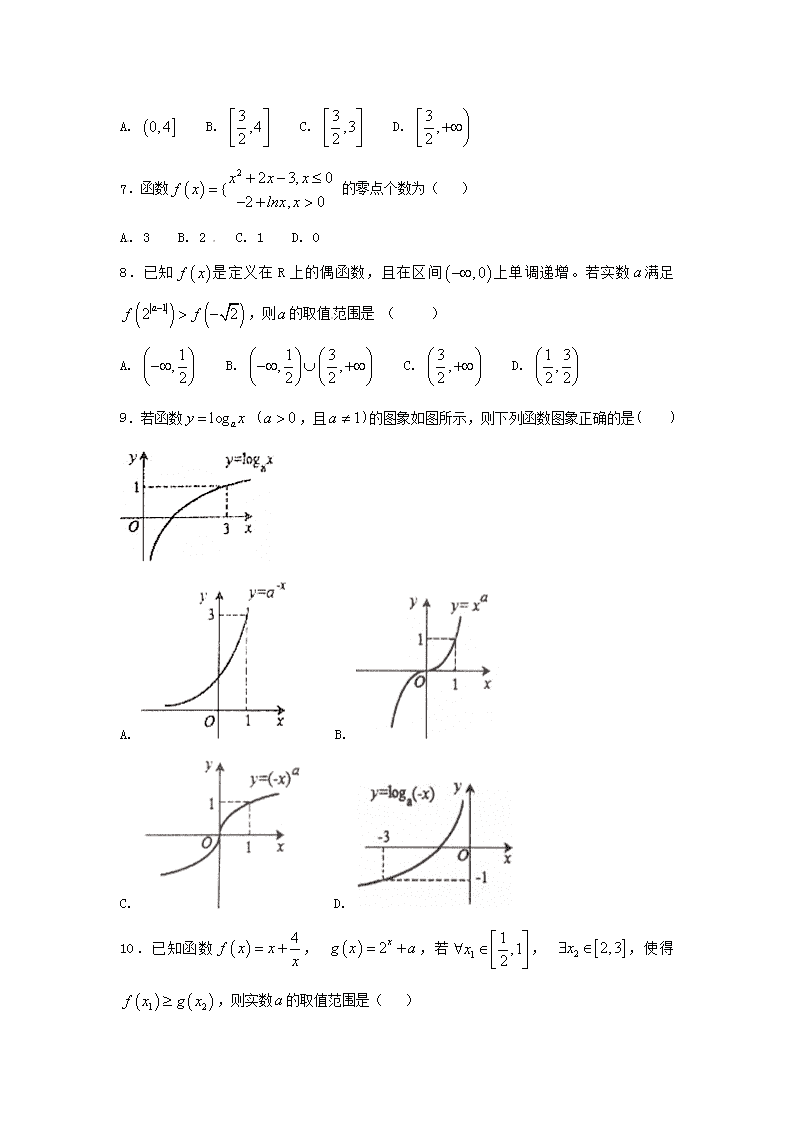
9.若函数 (,且)的图象如图所示,则下列函数图象正确的是( )
A. B.
C. D.
10.已知函数, ,若, ,使得,则实数的取值范围是( )
A. B. C. D.
11.已知是上的增函数,则a的取值范围是( )
A. B. C. D.
12.已知定义域为(-∞,0)∪(0,+∞)的函数f(x)是偶函数,并且在(-∞,0)上是增
函数,若f(-3)=0,则不等式<0的解集是 ( )
A. (-3,0 ) ∪(3,+∞) B. (-∞,-3 ) ∪(3,+∞)
C. (-3,0 ) ∪(0,3) D. (-∞,-3 ) ∪(0,3)
第II卷(非选择题 共90分)
二、填空题
(本大题共4小题,,每小题5分,共20分)
13.若命题:“ x∈R,kx2-kx-10”是假命题,则实数k的取值范围是________.
14.定义在上的函数,对任意都有,当 时,,则________.
15.已知函数是定义在区间上的偶函数,则函数的值域为 .
16.已知在上是的减函数,则的取值范围是_____.
三、解答题:本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17.(10分已知全集,集合.
(1)当时,求;
(2)当集合满足时,求实数的取值范围.
18.(12分)已知函数f(x)=2+log3x(1≤x≤9),函数g(x)=f2(x)+f(x2),求函数g(x)的值域.
19.(12分)设命题实数满足,其中,命题实数满足.
(1)若,且为真,求实数的取值范围.
(2)若是的充分不必要条件,求实数的取值范围.
20.(12分)已知命题函数在区间上是单调递增函数;命题不等式对任意实数恒成立.若是真命题,且为假命题,求实数的取值范围.
21.(12分)设函数是定义在上的函数,并且满足下面三个条件:①对任意正数,都有;②当时, ;③.
(1)求, 的值;【来源:全,品…中&高*考+网】
(2)证明在上是减函数;
(3)如果不等式成立,求的取值范围.
22.(12分)已知二次函数满足,且.
(1)求函数的解析式;
(2)令,求函数在上的最小值.
高三第一次检测文数答案
一.选择题 1——5.A B ADC 6——10C BD B A 11——12 D A
13. 14. 15. 16..
.
17.【解析】(1)由题意可解得;...... 5分
(2)由得实数的取值范围是.......10分
18. 试题解析:由已知函数f(x)的定义域为x∈{x|1≤x≤9},
则g(x)的定义域满足,【来源:全,品…中&高*考+网】
所以1≤x≤3,所以g(x)的定义域为{x||1≤x≤3}; .......4分
,
g(x)在x∈[1,3]单调递增,
则g(x)的最大值为g(x)max=g(3)=13,
g(x)的最小值为g(x)min=g(1)=6. .......12分
故g(x)的值域为[6,13].
19.试题解析:
由,其中,得, ,则, .
由,解得,即.
(1)若解得,若为真,则同时为真,
即,解得,∴实数的取值范围.......6分
(2)若是的充分不必要条件,即是的充分不必要条件,
∴,即,解得.........12分
20.试题解析. 若命题为真,则,
若命题为真,则或,即.
.......4分∵是真命题,且为假命题
∴真假或假真
∴或,即或 。。。。。12分
21.试题解析:(Ⅰ)令易得.
而,且,得. 。。。。。4分
(Ⅱ)
∴
∴在上为减函数. 。。。。。8分
(Ⅲ)由条件(1)及(Ⅰ)的结果得: ,其中,
由(Ⅱ)得: ,解得的范围是) 。。。。。12分
22. (1)设二次函数(),
则
∴, ,∴,
又,∴.
∴ 。。。。。5分
(2)①∵
∴.
又在上是单调函数,∴对称轴在区间的左侧或右侧,∴或
②, ,对称轴,
当时, ;
当时, ;
当时,
综上所述, 。。。。。12分