【数学】山东省滨州市博兴县第一中学2019-2020学年高一下学期开学检测试题（解析版） 13页

山东省滨州市博兴县第一中学2019-2020学年 高一下学期开学检测试题 一、单项选择题：本题共8小题，每小题5分，共40分．‎ ‎1.若复数满足：，则（ ）‎ A. 1 B. C. D. 2‎ ‎【答案】B ‎【解析】复数满足，则，‎ 由复数除法运算化简可得，‎ 由复数模的定义及运算可得，‎ 故选：B.‎ ‎2.已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图，其中B′O′＝C′O′＝1，A′O′＝，那么原△ABC的面积是(　　)‎ A. B. 2‎ C. D. ‎ ‎【答案】A ‎【解析】由题图可知原△ABC的高为AO＝，‎ ‎∴S△ABC＝×BC×OA＝×2×＝，故答案为A ‎3.若，且，那么是( )‎ A. 直角三角形 B. 等边三角形 C. 等腰三角形 D. 等腰直角三角形 ‎【答案】B ‎【解析】由题设可得 由题设可得，‎ 即该三角形是等边三角形，应选答案B．‎ ‎4.已知正方体的棱长为1，则该正方体外接球的体积与其内切球表面积之比为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】由正方体性质知，它的外接球的半径为，内切球的半径为，‎ ‎，‎ ‎：：2故选：D ‎5.如图所示，在正方形ABCD中，E为AB的中点，F为CE的中点，则 ‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】根据题意得：，又，，所以.‎ 故选D.‎ ‎6.设l是直线，，是两个不同的平面，下列命题正确的是（ ）‎ A. 若，，则 B. 若，，则 C. 若，，则 D. 若，，则 ‎【答案】D ‎【解析】A.若，，则与可能平行，也可能相交，所以不正确.‎ B.若，，则与可能的位置关系有相交、平行或,所以不正确.‎ C.若，，则可能，所以不正确.‎ D.若，，由线面平行的性质过的平面与相交于，则，又. 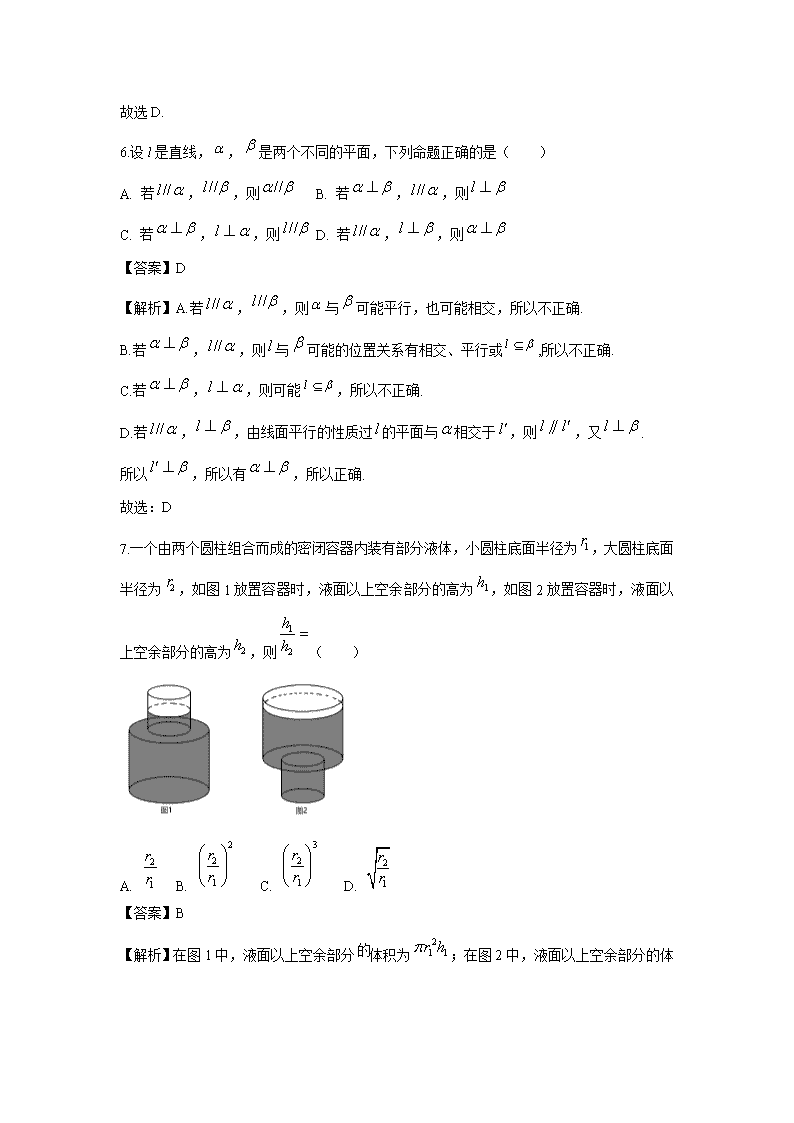所以，所以有，所以正确.‎ 故选：D ‎7.一个由两个圆柱组合而成的密闭容器内装有部分液体，小圆柱底面半径为，大圆柱底面半径为，如图1放置容器时，液面以上空余部分的高为，如图2放置容器时，液面以上空余部分的高为，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】在图1中，液面以上空余部分体积为；在图2‎ 中，液面以上空余部分的体积为.因为，所以.故选：B ‎8.已知三棱柱的侧棱与底面边长都相等，在底面内的射影为的中心，则与底面所成角的余弦值等于（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】如图所示，设三棱柱的侧棱与底面边长都等于.‎ 连接，则.‎ 在中，，得.‎ 在中，，即，‎ 则为等边三角形，所以.‎ 在菱形中，得.‎ 又因为点到底面的距离等于点到底面的距离 所以与底面所成角的正弦值为.‎ 即与底面所成角的余弦值为.‎ 故选：B 二、多项选择题：本题共4小题，每小题5分，共20分．‎ ‎9.（多选题）已知集合，其中i为虚数单位，则下列元素属于集合M的是（ ）‎ A. B. C. D. ‎ ‎【答案】BC ‎【解析】根据题意，中，‎ 时，；‎ 时，‎ ‎；时，；‎ 时，，‎ ‎.‎ 选项A中，；‎ 选项B中，；‎ 选项C中，；‎ 选项D中，.‎ 故选：BC.‎ ‎10.在下列向量组中，不能把向量表示出来的是（ ）‎ A. ， B. ，‎ C. ， D. ，‎ ‎【答案】ACD ‎【解析】对A，零向量与任何向量都是共线向量，故 ，不能做为一组基底，故A不能；‎ 对B，，∴ ，不共线，故B能．‎ 对C，∵，∴ ，不能做为一组基底，故C不能．‎ 对D，，∴，不能做为一组基底，故D不能．‎ 故选：ACD．‎ ‎11.下列说法正确的是（ ）‎ A. 在中，‎ B. 在中，若，则 C. 在中，若，则；若，则 D. 在中，‎ ‎【答案】ACD ‎【解析】对于A，由正弦定理，可得：‎ ‎，故A正确；‎ 对于B，由，可得，或，即，或，‎ ‎，或，故B错误；‎ 对于C，在中，由正弦定理可得，因此是的充要条件，故C正确；‎ 对于D，由正弦定理，‎ 可得右边左边，故D正确．‎ 故选：ACD．‎ ‎12.如图，在长方体中，，，，分别为棱，的中点，则下列说法正确的是（ ）‎ A. 四点共面 B. 平面平面 C. 直线与所成角的为 D. 平面 ‎【答案】BC ‎【解析】对于A，由图显然、是异面直线，故四点不共面，故A错误；‎ 对于B，由题意平面，故平面平面，故B正确；‎ 对于C，取的中点，连接、，可知三角形为等边三角形，故C正确； ‎ 对于D，平面，显然与平面不平行，故D错误；‎ 故选：BC 三、填空题：本题共4小题，每小题5分，共20分．‎ ‎13.设，则方程的解为_________.‎ ‎【答案】‎ ‎【解析】设（为虚数单位），‎ 则可化为，即，‎ 则，解得：，因此.‎ 故答案为：.‎ ‎14.设的内角，，的对边分别为，，，若，且，则的面积为______.‎ ‎【答案】‎ ‎【解析】由得，‎ 即，化简得，‎ ‎∵为三角形的内角，∴，‎ ‎∴，，故.‎ 故答案为：‎ ‎15.如图，一栋建筑物AB高（30-10）m，在该建筑物的正东方向有一个通信塔CD．在它们之间的地面M点（B、M、D三点共线）测得对楼顶A、塔顶C的仰角分别是15°和60°，在楼顶A处测得对塔顶C的仰角为30°，则通信塔CD的高为______m．‎ ‎【答案】60‎ ‎【解析】由题意可知：，，‎ 由三角形内角和定理可知.‎ 在中，.‎ 在中，由正弦定理可知：‎ ‎，‎ 在中，‎ ‎.‎ ‎16.已知平面向量，，，，且，若为平面单位向量，则的最小值为__________.‎ ‎【答案】‎ ‎【解析】由，，且，得，，设，，，，‎ 因为，所以，‎ 的最小值为.‎ 故答案为：‎ 四、解答题：本题共6小题，共70分．解答应写出文字说明 ‎17.已知，，.‎ ‎（1）求与的夹角；‎ ‎（2）求.‎ ‎【解】（1），，‎ ‎，‎ ‎，‎ ‎∴，∴，‎ ‎∴向量与的夹角.‎ ‎（2），‎ ‎.‎ ‎18.已知复数（为虚数单位）.‎ ‎（1）若，求复数的共轭复数；‎ ‎（2）若是关于的方程一个虚根，求实数的值.‎ ‎【解】（1）因为，所以，‎ 所以复数的共轭复数为.‎ ‎（2）因为是关于的方程的一个虚根，‎ 所以，即.‎ 又因为是实数，所以.‎ ‎19.如图，四棱锥的底面是边长为1的正方形，垂直于底面，.‎ ‎（1）求平面与平面所成二面角的大小；‎ ‎（2）设棱的中点为，求异面直线与所成角的大小.‎ ‎【解】（1）由题意可知底面是边长为1的正方形，则，‎ 又因为垂直于底面，平面，则，‎ 由于，则平面，‎ 而平面，所以，‎ 则即为平面与平面所成二面角的平面角，‎ 由可知，在中，；‎ ‎（2）由，且，为棱的中点，‎ 所以由等腰三角形性质可知,‎ 又因为，且，所以平面，‎ 而平面，所以，而且，‎ 所以平面，而平面，所以，‎ 则异面直线与垂直，所以异面直线与的夹角为.‎ ‎20.在锐角中，分别是角所对的边，且.‎ ‎（1）求角的大小；‎ ‎（2）若，且的面积为，求的值.‎ ‎【解】（1）因为 所以由正弦定理得,因为，‎ 所以,因为是锐角，所以.‎ ‎(2)由于，，又由于 ‎，，所以.‎ ‎21.如图，在平面直角坐标系中，，，．‎ ‎（1）求点B，C的坐标；‎ ‎（2）求证：四边形OABC为等腰梯形．‎ ‎【解】（1）设，则，‎ ‎，‎ ‎∴，‎ ‎∴，．‎ ‎（2）证明：连接OC．∵，，∴，∴．‎ 又，，∴四边形OABC为等腰梯形．‎ ‎22.如图，四棱锥中，平面分别为线段的中点.‎ ‎（1）求证：平面；‎ ‎（2）求证：平面平面 ‎【解】（1）‎ 设交点为，连接，又，‎ 又，所以四边形是菱形，则是中点，‎ 又为中点，是中位线，，‎ 平面，平面，平面；‎ ‎（2）由（1）可知四边形是菱形，，又平面可得，‎ 为中点可得，又，四边形为平行四边形，，‎ ‎，，平面，又平面，‎ 平面平面.‎