- 964.00 KB
- 2021-04-19 发布
绝密★启用前 试卷类型:A
2020届广东省韶关市高三调研测试
理科数学 2020.1.13
(本试卷分选择题和非选择题两部分,满分为150分,考试用时120分钟)
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1、已知全集,则( )
A、 B、 C、 D、
2、已知等差数列的前项和为,,则( )
A、 B、 C、 D、
3、设变量满足约束条件,则目标函数的最大值为( )
A、 B、 C、 D、
4、已知某地区中小学生人数和近视情况分别如图甲和图乙所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取4%的学生进行调查,则样本容量和抽取的初中生近视人数分别为( )
A、 B、 C、 D、
5、已知双曲线以椭圆的焦点为顶点,以椭圆的顶点为焦点,则双曲线的渐近线方程是( )
A、 B、 C、 D、
6、用数字组成没有重复数字的四位数,其中比3000大的奇数共有( )个
A、 B、 C、 D、
7、函数的部分图象大致为( )
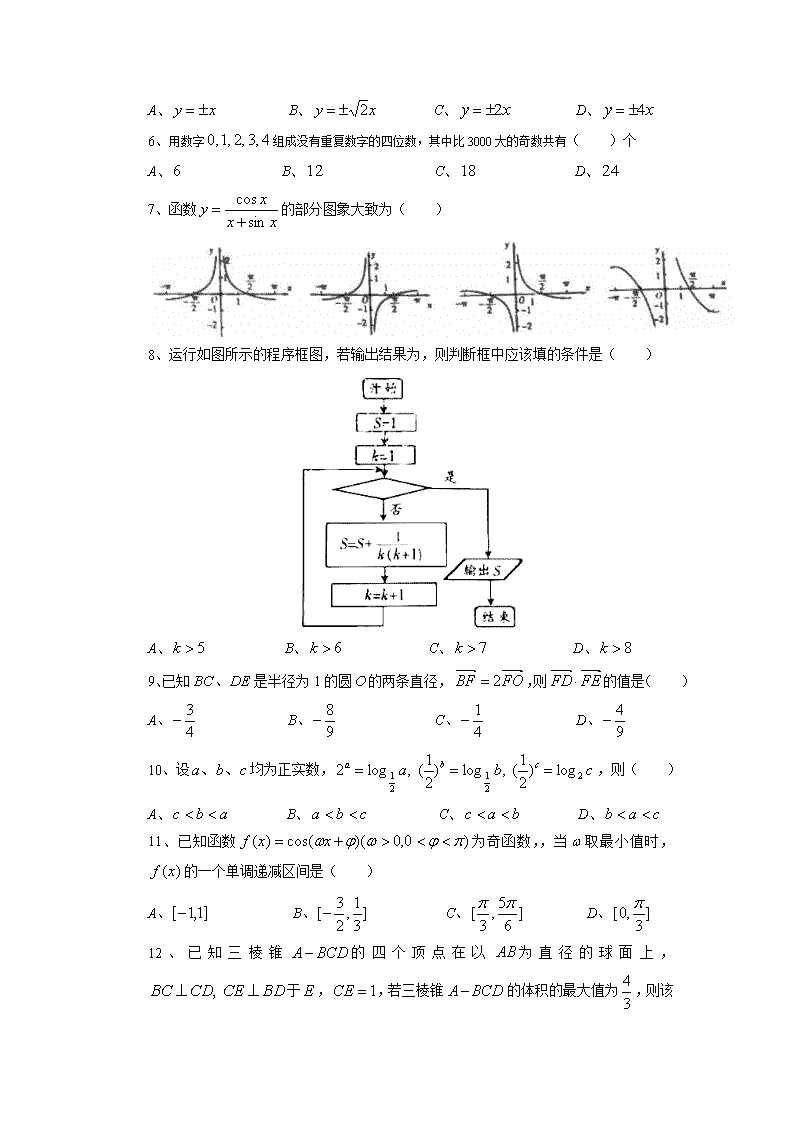
8、运行如图所示的程序框图,若输出结果为,则判断框中应该填的条件是( )
A、 B、 C、 D、
9、已知是半径为1的圆的两条直径,,则的值是( )
A、 B、 C、 D、
10、设均为正实数,,则( )
A、 B、 C、 D、
11、已知函数为奇函数,,当取最小值时,的一个单调递减区间是( )
A、 B、 C、 D、
12、已知三棱锥的四个顶点在以为直径的球面上,于,,若三棱锥的体积的最大值为
,则该球的表面积为( )
A、 B、 C、 D、
第II卷(非选择题,共90分)
本卷包括必考题和选考题,第(13)题~第(21)题为必考题,每个试题考生都必须作答,第(22)题~第(23)题为选考题,考生根据要求作答。
二、填空题:本题共4小题,每小题5分,共20分。
13、若,则 .
14、已知直线是曲线在处的切线,直线是曲线的一条切线,且,则直线的方程是 .
15、中国古代数学著作《算法统宗》中有这样一段记载:‘三百七十八里关,初行健步不难,次日脚痛减一半,六朝才得到其关’其大意为:有一个人走了378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地。则该人最后一天走的路程为 里.
16、离心率为的椭圆恰好过抛物线的焦点,为椭圆的上顶点,为直线上一动点,点关于直线的对称点为,则的最小值为 .
三、解答题:本大题共6小题,满分70分。解答应写出文字说明,证明过程或演算步骤。
17、(本小题满分12分)
如图,在平面四边形中,,设.
(1)若,求的值;
(2)用表示四边形的面积,并求的最大值.
18、(本小题满分12分)
如图,在四棱锥中,底面是正方形,侧棱底面,分别是的中点.
(1)求证:平面;
(2)设,求二面角的余弦值.
19、(本小题满分12分)
某电子工厂生产一种电子元件,产品出厂前要检出所有次品。已知这种电子元件次品率为0.01,且这种电子元件是否为次品相互独立。现要检测3000个这种电子元件,检测的流程是:先将这3000个电子元件分成个数相等的若干组,设每组有个电子元件,将每组的个电子元件串联起来,成组进行检测,若检测通过,则本组全部电子元件为正品,不需要再检测;若检测不通过,则本组至少有一个电子元件是次品,再对本组个电子元件逐一检测.
(1)当时,估算一组待检测电子元件中有次品的概率;
(2)设一组电子元件的检测次数为,求的数学期望;
(3)估算当为何值时,每个电子元件的检测次数最小,并估算此时检测的总次数(提示:利用进行估算).
20、(本小题满分12分)
已知椭圆的焦点在圆上,且椭圆上一点与两焦点围成的三角形周长为.
(1)求椭圆的方程;
(2)过圆上一点作圆的切线交椭圆于两点,证明:点在以为直径的圆内.
21、(本小题满分12分)
已知函数有两个极值点,且.
(1)求实数的取值范围;
(2)若,证明:.
(二)选考题:共10分.请学生在第22,23题中任选一题作答。如果多选,则按所做的第一题计分,作答时请用2B铅笔在答题卡上将所选题号后的方框涂黑.
22、[选修4-4:坐标系与参数方程](10分)
已知曲线的参数方程为(为参数),直线的极坐标方程为,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线的直角坐标方程和直线的普通方程;
(2)设点在曲线上,求点到直线距离的取值范围.
23、[选修4-5:不等式选讲](10分)
(1)已知函数,求不等式的解集;
(2)已知,求证:.
2020届韶关高三调研测试数学(理科)试题
参考答案和评分标准
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
A
B
A
C
C
B
B
B
A
C
二、填空题
13、 14、 15、 16、
三、解答题
17、解:(1)在中,由余弦定理知
由已知,
代入上式得:,即
又由正弦定理得:
即:,解得:……………………………………6分
(2)在中,由余弦定理知
故
所以
故………………………………………………………………12分
18、解:(1)证明:取的中点,连接
∵分别是的中点
∴
在正方形中,是的中点
∴
∴四边形是平行四边形
∴
又平面,平面
∴平面……………………………………………………………………………6分
(2)以为原点,延长线,所在直线分别为轴建立如图所示的空间坐标系,则
∴
设是平面的法向量,则
,令,得
设是平面的法向量,则
,令,得
由图形可知二面角为钝二面角
∴二面角的余弦值为……………………………………………………12分
19、解:(1)设事件:一组待检测电子元件中由次品,则事件表示一组待检测电子元件中没有次品
因为
所以…………………………4分
(2)依题意,的可能取值为
分布列如下:
1
所以的数学期望为:………………8分
(3)由(2)可得:每个元件的平均检验次数为:
因为
当且仅当时,检验次数最小
此时总检验次数(次)……………………………………
12分
20、(1)∵圆与轴的交点为,∴
∵椭圆上一点与两焦点围成的三角形周长为
∴ ∴ ∴
∴椭圆的方程为………………………………………………………………4分
(2)当直线的斜率不存在时,两点的坐标分别为
此时点到切线的距离为1,以为直径的圆的半径为
∵,∴点在以为直径的圆内;
当直线的斜率存在时,设直线的方程为
因为直线与圆相切,所以,即
联立,化简得:
∴……………………………………………………9分
∴
∴即 ∴点在以为直径的圆内
综上所述,点在以为直径的圆内。…………………………………………………12分
21、(1)的定义域为,
设,则在内有两个变号零点,
令得,令得
∴在递增,在递减
∴
又当时,,在没有两个零点
当时,
(令,因为,所以在递减,
)
∴使得,使得
当时,,∴递减
当时,,∴递增
当时,,∴递增;
当时,,递减
∴分别为的极小值与极大值点
综上,的取值范围为………………………………………………………………6分
(2)由(1)知,∴,∴
∴时,∴
要证,只需证
∵由(1)得
∴得,即
设,则,∴,∴
∴…………………………………………………………………………9分
下面说明
即,设
∴
∴递增,∴即
∴成立……………………………………………………………12分
22、 (1)由曲线的参数方程得:
曲线的普通方程为:…………………………………………………3分
由直线的极坐标方程得:
由代入上式得执行的直角坐标方程为…………5分
(2)由题意,可设点
到直线的距离
当时,,当时,
所以的取值范围是……………………………………………………10分
23、(1)当时,,解得
当时,,解得
当时,,无解
综上所述,不等式的解集为
(2)因为
所以(当且仅当取等号)
同理(当且仅当取等号)
(当且仅当取等号)
相加(当且仅当取等号)
所以
因为,所以
所以……………………………………………………………10分