【数学】2020届一轮复习（文）通用版9-5抛物线及其性质作业 14页

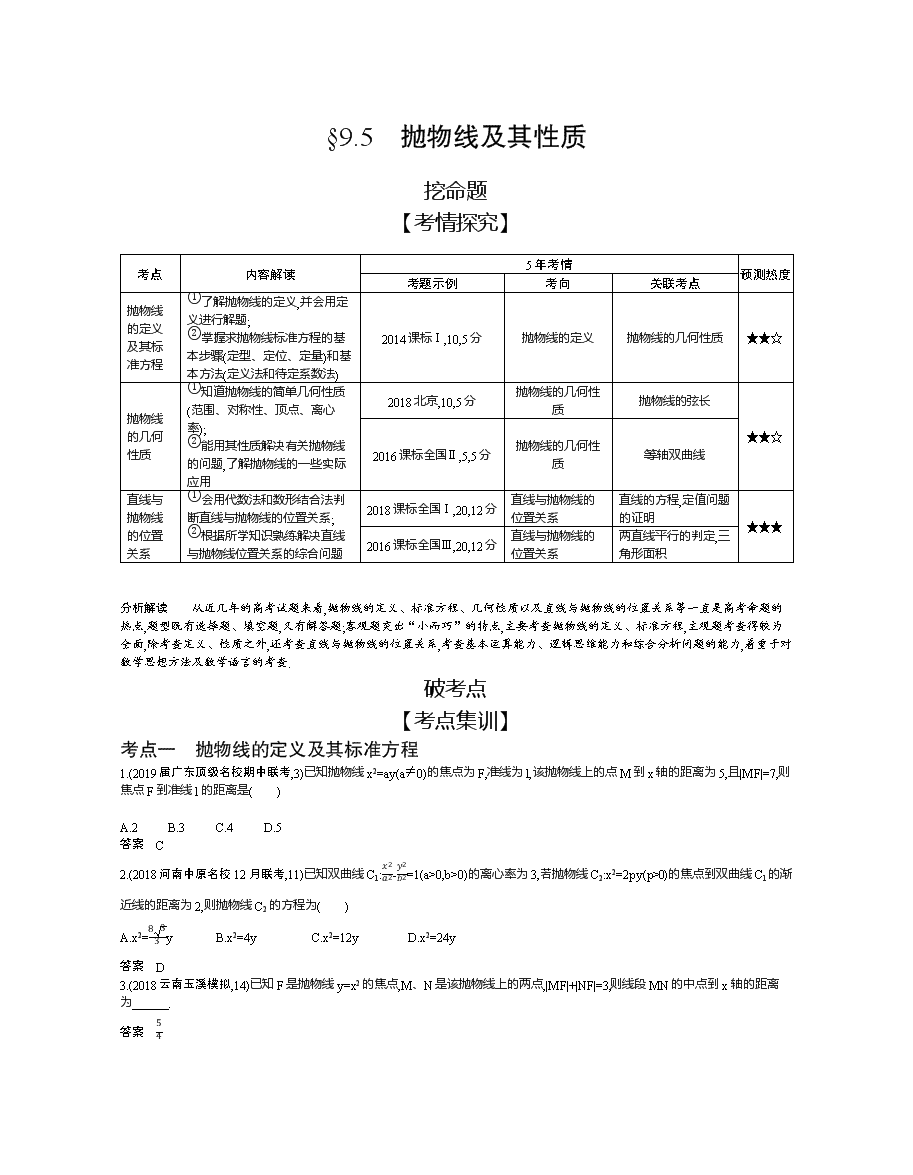
‎§9.5　抛物线及其性质 挖命题 ‎【考情探究】‎ 考点 内容解读 ‎5年考情 预测热度 考题示例 考向 关联考点 抛物线的定义及其标准方程 ‎①了解抛物线的定义,并会用定义进行解题;‎ ‎②掌握求抛物线标准方程的基本步骤(定型、定位、定量)和基本方法(定义法和待定系数法)‎ ‎2014课标Ⅰ,10,5分 抛物线的定义 抛物线的几何性质 ‎★★☆‎ 抛物线的几何性质 ‎①知道抛物线的简单几何性质(范围、对称性、顶点、离心率);‎ ‎②能用其性质解决有关抛物线的问题,了解抛物线的一些实际应用 ‎2018北京,10,5分 抛物线的几何性质 抛物线的弦长 ‎★★☆‎ ‎2016课标全国Ⅱ,5,5分 抛物线的几何性质 等轴双曲线 直线与抛物线的位置关系 ‎①会用代数法和数形结合法判断直线与抛物线的位置关系;‎ ‎②根据所学知识熟练解决直线与抛物线位置关系的综合问题 ‎2018课标全国Ⅰ,20,12分 直线与抛物线的位置关系 直线的方程,定值问题的证明 ‎★★★‎ ‎2016课标全国Ⅲ,20,12分 直线与抛物线的位置关系 两直线平行的判定,三角形面积 分析解读　　从近几年的高考试题来看,抛物线的定义、标准方程、几何性质以及直线与抛物线的位置关系等一直是高考命题的热点,题型既有选择题、填空题,又有解答题;客观题突出“小而巧”的特点,主要考查抛物线的定义、标准方程,主观题考查得较为全面,除考查定义、性质之外,还考查直线与抛物线的位置关系,考查基本运算能力、逻辑思维能力和综合分析问题的能力,着重于对数学思想方法及数学语言的考查.‎ 破考点 ‎【考点集训】‎ 考点一　抛物线的定义及其标准方程 ‎1.(2019届广东顶级名校期中联考,3)已知抛物线x2=ay(a≠0)的焦点为F,准线为l,该抛物线上的点M到x轴的距离为5,且|MF|=7,则焦点F到准线l的距离是(　　)‎ ‎　　　　　　　　　　　　 　　　　　　　　　　　　 　　　　　　　　　　　　 ‎ A.2 B.3 C.4 D.5‎ 答案　C　‎ ‎2.(2018河南中原名校12月联考,11)已知双曲线C1:x‎2‎a‎2‎-y‎2‎b‎2‎=1(a>0,b>0)的离心率为3,若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为(　　)‎ A.x2=‎8‎‎3‎‎3‎y B.x2=4y C.x2=12y D.x2=24y 答案　D　‎ ‎3.(2018云南玉溪模拟,14)已知F是抛物线y=x2的焦点,M、N是该抛物线上的两点,|MF|+|NF|=3,则线段MN的中点到x轴的距离为　　　. ‎ 答案　‎‎5‎‎4‎ 考点二　抛物线的几何性质 ‎1.(2015陕西,3,5分)已知抛物线y2=2px(p>0)的准线经过点(-1,1),则该抛物线焦点坐标为(　　)‎ A.(-1,0) B.(1,0) C.(0,-1) D.(0,1)‎ 答案　B　‎ ‎2.(2017广东中山一调,5)已知抛物线x2=2py(p>0)的准线与椭圆x‎2‎‎6‎+y‎2‎‎4‎=1相切,则p的值为(　　)‎ A.4 B.3 C.2 D.1‎ 答案　A　‎ ‎3.(2019届安徽皖中地区9月调研,9)抛物线E:y2=2px(p>0)的焦点为F,点A(0,2),若线段AF的中点B在抛物线上,则|BF|=(　　)‎ A.‎5‎‎4‎ B.‎5‎‎2‎ C.‎2‎‎2‎ D.‎‎3‎‎2‎‎4‎ 答案　D　‎ 考点三　直线与抛物线的位置关系 ‎1.(2019届安徽皖东第二次联考,8)若抛物线x2=2y在点a,‎a‎2‎‎2‎(a>0)处的切线与两条坐标轴围成的三角形的面积是8,则此切线方程是(　　)‎ A.x-4y-8=0 B.4x-y-8=0‎ C.x-4y+8=0 D.4x-y+8=0‎ 答案　B　‎ ‎2.(2014课标Ⅱ,10,5分)设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,则|AB|=(　　)‎ A.‎30‎‎3‎ B.6 C.12 D.7‎‎3‎ 答案　C　‎ ‎3.(2019届福建福州9月质检,9)抛物线C的顶点在原点,焦点在x轴上,直线x-y=0与抛物线C交于A、B两点,若P(1,1)为线段AB的中点,则抛物线C的方程为(　　)‎ A.y=2x2 B.y2=2x C.x2=2y D.y2=-2x 答案　B　‎ ‎4.(2018广东深圳二模,15)设过抛物线y2=2px(p>0)上任意一点P(异于原点O)的直线与抛物线y2=8px(p>0)交于A,B两点,直线OP与抛物线y2=8px(p>0)的另一个交点为Q,则S‎△ABQS‎△ABO=　　　　. ‎ 答案　3‎ 炼技法 ‎【方法集训】‎ 方法1　求抛物线的标准方程的方法 ‎　　　　　　　　　　　　 　　　　　　　　　　　　 　　　　　　　　　　　　 ‎ ‎1.(2018河南顶级名校12月联考,7)已知直线l过抛物线y2=-2px(p>0)的焦点,且与抛物线交于A、B两点,若线段AB的长是8,AB的中点到y轴的距离是2,则此抛物线的方程是(　　)‎ A.y2=-12x B.y2=-8x C.y2=-6x D.y2=-4x 答案　B　‎ ‎2.(2019届湖南八校第一次调研,9)在平面直角坐标系xOy中,动点P到圆(x-2)2+y2=1上的点的最小距离与其到直线x=-1的距离相等,则P点的轨迹方程是(　　)‎ A.y2=8x B.x2=8y C.y2=4x D.x2=4y 答案　A　‎ ‎3.(2017河北六校模拟,14)抛物线C:y2=2px(p>0)的焦点为F,点O是坐标原点,过点O,F的圆与抛物线C的准线相切,且该圆的面积为36π,则抛物线的方程为　　　　. ‎ 答案　y2=16x 方法2　抛物线定义的应用策略 ‎1.(2014课标Ⅰ,10,5分)已知抛物线C:y2=x的焦点为F,A(x0,y0)是C上一点,|AF|=‎5‎‎4‎x0,则x0=(　　)　　　　　　　　　　　 　　　　　　　　　　　　 　　　　　　　　　　　　 ‎ A.1 B.2 C.4 D.8‎ 答案　A　‎ ‎2.过抛物线y2=2px(p>0)的焦点F的直线l与抛物线交于B、C两点,l与抛物线的准线交于点A,且|AF|=6,AF=2FB,则|BC|=(　　)‎ A.8 B.‎13‎‎2‎ C.6 D.‎‎9‎‎2‎ 答案　D　‎ ‎3.(2019届河南顶级名校高三入学测试,15)抛物线y2=8x的焦点为F,点A(6,3),P为抛物线上一点,且P不在直线AF上,则△PAF周长的最小值为　　　　. ‎ 答案　13‎ 方法3　与直线和抛物线位置关系有关问题的求解方法 ‎1.(2018福建莆田模拟,6)已知O为坐标原点,F为抛物线C:y2=8x的焦点,过F作直线l与C交于A,B两点.若|AB|=10,则△OAB的重心的横坐标为(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.‎4‎‎3‎ B.2 C.‎8‎‎3‎ D.3‎ 答案　B　‎ ‎2.(2018湖北武汉模拟,9)过点P(2,-1)作抛物线x2=4y的两条切线,切点分别为A,B,PA,PB分别交x轴于E,F两点,O为坐标原点,则△PEF与△OAB的面积之比为(　　)‎ A.‎3‎‎2‎ B.‎3‎‎3‎ C.‎1‎‎2‎ D.‎‎3‎‎4‎ 答案　C　‎ ‎3.(2019届河南洛阳期中检测,20)已知抛物线C:x2=2py(p>0)的焦点为F,抛物线上一点P的纵坐标为3,且|PF|=4,过M(m,0)作抛物线C的切线MA(斜率不为0),切点为A.‎ ‎(1)求抛物线C的方程;‎ ‎(2)求证:以FA为直径的圆过点M.‎ 解析　(1)∵|PF|=yP+p‎2‎,∴4=3+p‎2‎,∴p=2.‎ ‎∴抛物线C的方程为x2=4y.(4分)‎ ‎(2)证明:设Ax‎0‎‎,‎x‎0‎‎2‎‎4‎(x0≠0),切线MA的斜率为k(k≠0).‎ ‎∵x2=4y,∴y=x‎2‎‎4‎,‎ ‎∴y'=x‎2‎,∴k=x‎0‎‎2‎.(5分)‎ ‎∴切线MA的方程为y-x‎0‎‎2‎‎4‎=x‎0‎‎2‎(x-x0),即y=x‎0‎‎2‎x-x‎0‎‎2‎‎4‎.(6分)‎ ‎∵切线过M(m,0),∴x‎0‎m‎2‎-x‎0‎‎2‎‎4‎=0.‎ 又∵x0≠0,∴x0=2m.(8分)‎ ‎∵F(0,1),M(m,0),Ax‎0‎‎,‎x‎0‎‎2‎‎4‎(x0≠0),‎ ‎∴MF·MA=(-m,1)·x‎0‎‎-m,‎x‎0‎‎2‎‎4‎=(-m,1)·(m,m2)=0,(10分)‎ ‎∴∠FMA=90°,‎ 因此,以FA为直径的圆过点M.(12分)‎ 过专题 ‎【五年高考】‎ A组　统一命题·课标卷题组 ‎1.(2016课标全国Ⅱ,5,5分)设F为抛物线C:y2=4x的焦点,曲线y=kx(k>0)与C交于点P,PF⊥x轴,则k=(　　)　　　　　　　　　　　　 　　　　　　　　　　　　 　　　　　　　　　　　　 ‎ A.‎1‎‎2‎ B.1 C.‎3‎‎2‎ D.2‎ 答案　D　‎ ‎2.(2018课标全国Ⅰ,20,12分)设抛物线C:y2=2x,点A(2,0),B(-2,0),过点A的直线l与C交于M,N两点.‎ ‎(1)当l与x轴垂直时,求直线BM的方程;‎ ‎(2)证明:∠ABM=∠ABN.‎ 解析　(1)当l与x轴垂直时,l的方程为x=2,可得M的坐标为(2,2)或(2,-2).‎ 所以直线BM的方程为y=‎1‎‎2‎x+1或y=-‎1‎‎2‎x-1.‎ ‎(2)证明:当l与x轴垂直时,AB为MN的垂直平分线,所以∠ABM=∠ABN.‎ 当l与x轴不垂直时,设l的方程为y=k(x-2)(k≠0),M(x1,y1),N(x2,y2),则x1>0,x2>0.‎ 由y=k(x-2),‎y‎2‎‎=2x得ky2-2y-4k=0,可知y1+y2=‎2‎k,y1y2=-4.‎ 直线BM,BN的斜率之和为 kBM+kBN=y‎1‎x‎1‎‎+2‎+y‎2‎x‎2‎‎+2‎=x‎2‎y‎1‎‎+x‎1‎y‎2‎+2(y‎1‎+y‎2‎)‎‎(x‎1‎+2)(x‎2‎+2)‎.①‎ 将x1=y‎1‎k+2,x2=y‎2‎k+2及y1+y2,y1y2的表达式代入①式分子,可得x2y1+x1y2+2(y1+y2)=‎2y‎1‎y‎2‎+4k(y‎1‎+y‎2‎)‎k=‎-8+8‎k=0.‎ 所以kBM+kBN=0,可知BM,BN的倾斜角互补,所以∠ABM=∠ABN.‎ 综上,∠ABM=∠ABN.‎ ‎3.(2016课标全国Ⅲ,20,12分)已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1,l2分别交C于A,B两点,交C的准线于P,Q两点.‎ ‎(1)若F在线段AB上,R是PQ的中点,证明AR∥FQ;‎ ‎(2)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.‎ 解析　由题设知F‎1‎‎2‎‎,0‎.设l1:y=a,l2:y=b,易知ab≠0,‎ 且Aa‎2‎‎2‎‎,a,Bb‎2‎‎2‎‎,b,P‎-‎1‎‎2‎,a,Q‎-‎1‎‎2‎,b,R‎-‎1‎‎2‎,‎a+b‎2‎.‎ 记过A,B两点的直线为l,则l的方程为2x-(a+b)y+ab=0.(3分)‎ ‎(1)证明:由于F在线段AB上,故1+ab=0.‎ 记AR的斜率为k1,FQ的斜率为k2,则 k1=a-b‎1+‎a‎2‎=a-ba‎2‎‎-ab=‎1‎a=‎-aba=-b=k2.‎ 所以AR∥FQ.(5分)‎ ‎(2)设l与x轴的交点为D(x1,0),则S△ABF=‎1‎‎2‎|b-a||FD|=‎1‎‎2‎|b-a|x‎1‎‎-‎‎1‎‎2‎,S△PQF=‎|a-b|‎‎2‎.‎ 由题设可得2×‎1‎‎2‎|b-a|x‎1‎‎-‎‎1‎‎2‎=‎|a-b|‎‎2‎,‎ 所以x1=0(舍去)或x1=1.‎ 设满足条件的AB的中点为E(x,y).‎ 当AB与x轴不垂直时,‎ 由kAB=kDE可得‎2‎a+b=yx-1‎(x≠1).‎ 而a+b‎2‎=y,所以y2=x-1(x≠1).‎ 当AB与x轴垂直时,E与D重合.‎ 所以,所求轨迹方程为y2=x-1.(12分)‎ B组　自主命题·省(区、市)卷题组 考点一　抛物线的定义及其标准方程 ‎1.(2014辽宁,8,5分)已知点A(-2,3)在抛物线C:y2=2px的准线上,记C的焦点为F,则直线AF的斜率为(　　)　　　　　　　　　　　　 　　　　　　　　　　　　 　　　　　　　　　　　　 ‎ A.-‎4‎‎3‎ B.-1 C.-‎3‎‎4‎ D.-‎‎1‎‎2‎ 答案　C　‎ ‎2.(2016浙江,19,15分)如图,设抛物线y2=2px(p>0)的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1.‎ ‎(1)求p的值;‎ ‎(2)若直线AF交抛物线于另一点B,过B与x轴平行的直线和过F与AB垂直的直线交于点N,AN与x轴交于点M.求M的横坐标的取值范围.‎ 解析　(1)由题意可得,抛物线上点A到焦点F的距离等于点A到直线x=-1的距离,由抛物线的定义得p‎2‎=1,即p=2.‎ ‎(2)由(1)得,抛物线方程为y2=4x,F(1,0),可设A(t2,2t),t≠0,t≠±1.‎ 因为AF不垂直于y轴,可设直线AF:x=sy+1(s≠0),由y‎2‎‎=4x,‎x=sy+1‎消去x得y2-4sy-4=0,‎ 故y1y2=-4,所以,B‎1‎t‎2‎‎,-‎‎2‎t.‎ 又直线AB的斜率为‎2tt‎2‎‎-1‎,故直线FN的斜率为-t‎2‎‎-1‎‎2t.‎ 从而得直线FN:y=-t‎2‎‎-1‎‎2t(x-1),直线BN:y=-‎2‎t.‎ 所以Nt‎2‎‎+3‎t‎2‎‎-1‎‎,-‎‎2‎t.‎ 设M(m,0),由A,M,N三点共线得 ‎2tt‎2‎‎-m‎=‎2t+‎‎2‎tt‎2‎‎-‎t‎2‎‎+3‎t‎2‎‎-1‎,‎ 于是m=‎2‎t‎2‎t‎2‎‎-1‎.‎ 所以m<0或m>2.‎ 经检验,m<0或m>2满足题意.‎ 综上,点M的横坐标的取值范围是(-∞,0)∪(2,+∞).‎ 思路分析　(1)利用抛物线的定义来解题;(2)由(1)知抛物线的方程,可设A点坐标及直线AF的方程,与抛物线方程联立可得B点坐标,进而得直线FN的方程与直线BN的方程,联立可得N点坐标,最后利用A,M,N三点共线可得kAN=kAM,最终求出结果.‎ 考点二　抛物线的几何性质 ‎1.(2016四川,3,5分)抛物线y2=4x的焦点坐标是(　　)　　　　　　　　　　　 　　　　　　　　　　　　 　　　　　　　　　　　　 ‎ A.(0,2) B.(0,1) C.(2,0) D.(1,0)‎ 答案　D　‎ ‎2.(2014安徽,3,5分)抛物线y=‎1‎‎4‎x2的准线方程是(　　)‎ A.y=-1 B.y=-2‎ C.x=-1 D.x=-2‎ 答案　A　‎ ‎3.(2018北京,10,5分)已知直线l过点(1,0)且垂直于x轴.若l被抛物线y2=4ax截得的线段长为4,则抛物线的焦点坐标为　　　　. ‎ 答案　(1,0)‎ ‎4.(2017天津,12,5分)设抛物线y2=4x的焦点为F,准线为l.已知点C在l上,以C为圆心的圆与y轴的正半轴相切于点A.若∠FAC=120°,则圆的方程为　　　　　　　　. ‎ 答案　(x+1)2+(y-‎3‎)2=1‎ 考点三　直线与抛物线的位置关系 ‎1.(2014湖南,14,5分)平面上一机器人在行进中始终保持与点F(1,0)的距离和到直线x=-1的距离相等.若机器人接触不到过点P(-1,0)且斜率为k的直线,则k的取值范围是　　　　　　　. ‎ 答案　(-∞,-1)∪(1,+∞)‎ ‎2.(2015浙江,19,15分)如图,已知抛物线C1:y=‎1‎‎4‎x2,圆C2:x2+(y-1)2=1,过点P(t,0)(t>0)作不过原点O的直线PA,PB分别与抛物线C1和圆C2相切,A,B为切点.‎ ‎(1)求点A,B的坐标;‎ ‎(2)求△PAB的面积.‎ 注:直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则称该直线与抛物线相切,称该公共点为切点.‎ 解析　(1)由题意知直线PA的斜率存在,故可设直线PA的方程为y=k(x-t),‎ 由y=k(x-t),‎y=‎‎1‎‎4‎x‎2‎消去y,整理得x2-4kx+4kt=0,‎ 由于直线PA与抛物线相切,得k=t.‎ 因此,点A的坐标为(2t,t2).‎ 设圆C2的圆心为D(0,1),点B的坐标为(x0,y0),由题意知:点B,O关于直线PD对称,故y‎0‎‎2‎‎=-x‎0‎‎2t+1,‎x‎0‎t-y‎0‎=0,‎ 解得x‎0‎‎=‎2t‎1+‎t‎2‎,‎y‎0‎‎=‎2‎t‎2‎‎1+‎t‎2‎.‎ 因此,点B的坐标为‎2t‎1+‎t‎2‎‎,‎‎2‎t‎2‎‎1+‎t‎2‎.‎ ‎(2)由(1)知|AP|=t·‎1+‎t‎2‎,‎ 和直线PA的方程tx-y-t2=0.‎ 点B到直线PA的距离是d=t‎2‎‎1+‎t‎2‎,‎ 设△PAB的面积为S(t),所以S(t)=‎1‎‎2‎|AP|·d=t‎3‎‎2‎.‎ C组　教师专用题组 考点一　抛物线的定义及其标准方程 ‎1.(2013课标Ⅰ,8,5分)O为坐标原点,F为抛物线C:y2=4‎2‎x的焦点,P为C上一点,若|PF|=4‎2‎,则△POF的面积为(　　)　　　　　　　　　　　　 　　　　　　　　　　　　 　　　　　　　　　　　　 ‎ A.2 B.2‎2‎ C.2‎3‎ D.4‎ 答案　C　‎ ‎2.(2011课标,9,5分)已知直线l过抛物线C的焦点,且与C的对称轴垂直,l与C交于A,B两点,|AB|=12,P为C的准线上一点,则△ABP的面积为(　　)‎ A.18 B.24‎ C.36 D.48‎ 答案　C　‎ ‎3.(2017山东,15,5分)在平面直角坐标系xOy中,双曲线x‎2‎a‎2‎-y‎2‎b‎2‎=1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点.若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为　　　　　　. ‎ 答案　y=±‎2‎‎2‎x 考点二　抛物线的几何性质 ‎1.(2013课标Ⅱ,10,5分)设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点.若|AF|=3|BF|,则l的方程为(　　)‎ A.y=x-1或y=-x+1‎ B.y=‎3‎‎3‎(x-1)或y=-‎3‎‎3‎(x-1)‎ C.y=‎3‎(x-1)或y=-‎3‎(x-1)‎ D.y=‎2‎‎2‎(x-1)或y=-‎2‎‎2‎(x-1)‎ 答案　C　‎ ‎2.(2014陕西,11,5分)抛物线y2=4x的准线方程为　　　　. ‎ 答案　x=-1‎ ‎3.(2014上海,4,4分)若抛物线y2=2px的焦点与椭圆x‎2‎‎9‎+y‎2‎‎5‎=1的右焦点重合,则该抛物线的准线方程为　　　　. ‎ 答案　x=-2‎ 考点三　直线与抛物线的位置关系 ‎1.(2015四川,10,5分)设直线l与抛物线y2=4x相交于A,B两点,与圆(x-5)2+y2=r2(r>0)相切于点M,且M为线段AB的中点.若这样的直线l恰有4条,则r的取值范围是(　　)‎ A.(1,3) B.(1,4) C.(2,3) D.(2,4)‎ 答案　D　‎ ‎2.(2014四川,10,5分)已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧,OA·OB=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是(　　)‎ A.2 B.3 C.‎17‎‎2‎‎8‎ D.‎‎10‎ 答案　B　‎ ‎3.(2014浙江,22,14分)已知△ABP的三个顶点都在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点,PF=3FM.‎ ‎(1)若|PF|=3,求点M的坐标;‎ ‎(2)求△ABP面积的最大值.‎ 解析　(1)由题意知焦点F(0,1),准线方程为y=-1.‎ 设P(x0,y0),由抛物线定义知|PF|=y0+1,得到y0=2,‎ 所以P(2‎2‎,2)或P(-2‎2‎,2).‎ 由PF=3FM,分别得M‎-‎2‎‎2‎‎3‎,‎‎2‎‎3‎或M‎2‎‎2‎‎3‎‎,‎‎2‎‎3‎.‎ ‎(2)设直线AB的方程为y=kx+m,点A(x1,y1),B(x2,y2),P(x0,y0).‎ 由y=kx+m,‎x‎2‎‎=4y得x2-4kx-4m=0,‎ 于是Δ=16k2+16m>0,x1+x2=4k,x1x2=-4m,‎ 所以AB中点M的坐标为(2k,2k2+m).‎ 由PF=3FM,得(-x0,1-y0)=3(2k,2k2+m-1),‎ 所以x‎0‎‎=-6k,‎y‎0‎‎=4-6k‎2‎-3m,‎由x‎0‎‎2‎=4y0得k2=-‎1‎‎5‎m+‎4‎‎15‎.‎ 由Δ>0,k2≥0,得-‎1‎‎3‎f‎4‎‎3‎,‎ 所以,当m=‎1‎‎9‎时, f(m)取到最大值‎256‎‎243‎,此时k=±‎55‎‎15‎.‎ 所以,△ABP面积的最大值为‎256‎‎5‎‎135‎.‎ ‎4.(2014福建,21,12分)已知曲线Γ上的点到点F(0,1)的距离比它到直线y=-3的距离小2.‎ ‎(1)求曲线Γ的方程;‎ ‎(2)曲线Γ在点P处的切线l与x轴交于点A,直线y=3分别与直线l及y轴交于点M,N.以MN为直径作圆C,过点A作圆C的切线,切点为B.试探究:当点P在曲线Γ上运动(点P与原点不重合)时,线段AB的长度是否发生变化?证明你的结论.‎ 解析　(1)解法一:设S(x,y)为曲线Γ上任意一点,‎ 依题意,点S到F(0,1)的距离与它到直线y=-1的距离相等,‎ 所以曲线Γ是以点F(0,1)为焦点、直线y=-1为准线的抛物线,所以曲线Γ的方程为x2=4y.‎ 解法二:设S(x,y)为曲线Γ上任意一点,‎ 则|y-(-3)|-‎(x-0‎)‎‎2‎+(y-1‎‎)‎‎2‎=2,‎ 依题意,知点S(x,y)只能在直线y=-3的上方,所以y>-3,‎ 所以‎(x-0‎)‎‎2‎+(y-1‎‎)‎‎2‎=y+1,‎ 化简得,曲线Γ的方程为x2=4y.‎ ‎(2)当点P在曲线Γ上运动时,线段AB的长度不变.证明如下:‎ 由(1)知抛物线Γ的方程为y=‎1‎‎4‎x2,‎ 设P(x0,y0)(x0≠0),则y0=‎1‎‎4‎x‎0‎‎2‎,‎ 由y'=‎1‎‎2‎x,得切线l的斜率k=y'‎|‎x=‎x‎0‎=‎1‎‎2‎x0,‎ 所以切线l的方程为y-y0=‎1‎‎2‎x0(x-x0),即y=‎1‎‎2‎x0x-‎1‎‎4‎x‎0‎‎2‎.‎ 由y=‎1‎‎2‎x‎0‎x-‎1‎‎4‎x‎0‎‎2‎,‎y=0‎得A‎1‎‎2‎x‎0‎‎,0‎.‎ 由y=‎1‎‎2‎x‎0‎x-‎1‎‎4‎x‎0‎‎2‎,‎y=3‎得M‎1‎‎2‎x‎0‎‎+‎6‎x‎0‎,3‎.‎ 又N(0,3),所以圆心C‎1‎‎4‎x‎0‎‎+‎3‎x‎0‎,3‎,‎ 半径r=‎1‎‎2‎|MN|=‎1‎‎4‎x‎0‎‎+‎‎3‎x‎0‎,‎ ‎|AB|=‎‎|AC‎|‎‎2‎-‎r‎2‎ ‎=‎1‎‎2‎x‎0‎‎-‎‎1‎‎4‎x‎0‎‎+‎‎3‎x‎0‎‎2‎‎+‎3‎‎2‎-‎‎1‎‎4‎x‎0‎‎+‎‎3‎x‎0‎‎2‎=‎6‎.‎ 所以点P在曲线Γ上运动时,线段AB的长度不变.‎ ‎5.(2014湖北,22,14分)在平面直角坐标系xOy中,点M到点F(1,0)的距离比它到y轴的距离多1.记点M的轨迹为C.‎ ‎(1)求轨迹C的方程;‎ ‎(2)设斜率为k的直线l过定点P(-2,1).求直线l与轨迹C恰好有一个公共点、两个公共点、三个公共点时k的相应取值范围.‎ 解析　(1)设点M(x,y),依题意得|MF|=|x|+1,即‎(x-1‎)‎‎2‎+‎y‎2‎=|x|+1,‎ 化简整理得y2=2(|x|+x).‎ 故点M的轨迹C的方程为y2=‎‎4x,x≥0,‎‎0,x<0.‎ ‎(2)在点M的轨迹C中,记C1:y2=4x,C2:y=0(x<0),‎ 依题意,可设直线l的方程为y-1=k(x+2).‎ 由方程组y-1=k(x+2),‎y‎2‎‎=4x,‎ 可得ky2-4y+4(2k+1)=0.①‎ ‎(i)当k=0时,y=1.把y=1代入轨迹C的方程,得x=‎1‎‎4‎.‎ 故此时直线l:y=1与轨迹C恰好有一个公共点‎1‎‎4‎‎,1‎.‎ ‎(ii)当k≠0时,方程①的判别式为Δ=-16(2k2+k-1).②‎ 设直线l与x轴的交点为(x0,0),则 由y-1=k(x+2),令y=0,得x0=-‎2k+1‎k.③‎ 若Δ<0,‎x‎0‎‎<0,‎由②③解得k<-1或k>‎1‎‎2‎,‎ 即当k∈(-∞,-1)∪‎1‎‎2‎‎,+∞‎时,直线l与C1没有公共点,与C2有一个公共点,‎ 故此时直线l与轨迹C恰好有一个公共点.‎ 若Δ=0,‎x‎0‎‎<0‎或Δ>0,‎x‎0‎‎≥0,‎ 由②③解得k∈‎-1,‎‎1‎‎2‎或-‎1‎‎2‎≤k<0,‎ 即当k∈‎-1,‎‎1‎‎2‎时,直线l与C1只有一个公共点,与C2有一个公共点.‎ 当k∈‎-‎1‎‎2‎,0‎时,直线l与C1有两个公共点,与C2没有公共点.‎ 故当k∈‎-‎1‎‎2‎,0‎∪‎-1,‎‎1‎‎2‎时,直线l与轨迹C恰好有两个公共点.‎ 若Δ>0,‎x‎0‎‎<0,‎由②③解得-10)的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且|QF|=‎5‎‎4‎|PQ|.‎ ‎(1)求C的方程;‎ ‎(2)过F的直线l与C相交于A、B两点,若AB的垂直平分线l'与C相交于M、N两点,且A、M、B、N四点在同一圆上,求l的方程.‎ 解析　(1)设Q(x0,4),代入y2=2px得x0=‎8‎p.‎ 所以|PQ|=‎8‎p,|QF|=p‎2‎+x0=p‎2‎+‎8‎p.‎ 由题设得p‎2‎+‎8‎p=‎5‎‎4‎×‎8‎p,解得p=-2(舍去)或p=2.‎ 所以C的方程为y2=4x.(5分)‎ ‎(2)依题意知l与坐标轴不垂直,故可设l的方程为x=my+1(m≠0).代入y2=4x得y2-4my-4=0.‎ 设A(x1,y1),B(x2,y2),则y1+y2=4m,y1y2=-4.‎ 故AB的中点为D(2m2+1,2m),|AB|=m‎2‎‎+1‎|y1-y2|=4(m2+1).‎ 又l'的斜率为-m,所以l'的方程为x=-‎1‎my+2m2+3.‎ 将上式代入y2=4x,并整理得y2+‎4‎my-4(2m2+3)=0.‎ 设M(x3,y3),N(x4,y4).则y3+y4=-‎4‎m,y3y4=-4(2m2+3).‎ 故MN的中点为E‎2‎m‎2‎‎+2m‎2‎+3,-‎‎2‎m,|MN|=‎1+‎‎1‎m‎2‎|y3-y4|=‎4(m‎2‎+1)‎‎2m‎2‎+1‎m‎2‎.(10分)‎ 由于MN垂直平分AB,故A、M、B、N四点在同一圆上等价于|AE|=|BE|=‎1‎‎2‎|MN|,从而‎1‎‎4‎|AB|2+|DE|2=‎1‎‎4‎|MN|2,‎ 即4(m2+1)2+‎2m+‎‎2‎m‎2‎+‎2‎m‎2‎‎+2‎‎2‎=‎4(m‎2‎+1‎)‎‎2‎(2m‎2‎+1)‎m‎4‎,‎ 化简得m2-1=0,解得m=1或m=-1.‎ 所求直线l的方程为x-y-1=0或x+y-1=0.(12分)‎ ‎7.(2012课标全国,20,12分)设抛物线C:x2=2py(p>0)的焦点为F,准线为l.A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.‎ ‎(1)若∠BFD=90°,△ABD的面积为4‎2‎,求p的值及圆F的方程;‎ ‎(2)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.‎ 解析　(1)由已知可得△BFD为等腰直角三角形,|BD|=2p,圆F的半径|FA|=‎2‎p.‎ 由抛物线定义可知A到l的距离d=|FA|=‎2‎p.‎ 因为△ABD的面积为4‎2‎,所以‎1‎‎2‎|BD|·d=4‎2‎,即‎1‎‎2‎·2p·‎2‎p=4‎2‎,‎ 解得p=-2(舍去)或p=2.‎ 所以F(0,1),圆F的方程为x2+(y-1)2=8.‎ ‎(2)因为A,B,F三点在同一直线m上,所以AB为圆F的直径,∠ADB=90°.‎ 由抛物线定义知|AD|=|FA|=‎1‎‎2‎|AB|,‎ 所以∠ABD=30°,m的斜率为‎3‎‎3‎或-‎3‎‎3‎.‎ 当m的斜率为‎3‎‎3‎时,由已知可设n:y=‎3‎‎3‎x+b,代入x2=2py得x2-‎2‎‎3‎‎3‎px-2pb=0.‎ 由于n与C只有一个公共点,故Δ=‎4‎‎3‎p2+8pb=0.解得b=-p‎6‎.‎ 因为m在y轴上的截距b1=p‎2‎,所以‎|b‎1‎|‎‎|b|‎=3,所以坐标原点到m,n距离的比值为3.当m的斜率为-‎3‎‎3‎时,由图形对称性可知,坐标原点到m,n距离的比值为3.‎ ‎8.(2010全国Ⅰ,22,12分)已知抛物线C:y2=4x的焦点为F,过点K(-1,0)的直线l与C相交于A、B两点,点A关于x轴的对称点为D.‎ ‎(1)证明:点F在直线BD上;‎ ‎(2)设FA·FB=‎8‎‎9‎,求△BDK的内切圆M的方程.‎ 解析　设A(x1,y1),B(x2,y2),D(x1,-y1),l的方程为x=my-1(m≠0).‎ ‎(1)证明:将x=my-1代入y2=4x并整理得y2-4my+4=0,‎ 从而y1+y2=4m,y1y2=4.①‎ 直线BD的方程为y-y2=y‎2‎‎+‎y‎1‎x‎2‎‎-‎x‎1‎·(x-x2),‎ 即y-y2=‎4‎y‎2‎‎-‎y‎1‎·x-‎y‎2‎‎2‎‎4‎.‎ 令y=0,得x=y‎1‎y‎2‎‎4‎=1.所以点F(1,0)在直线BD上.‎ ‎(2)由(1)知,‎ x1+x2=(my1-1)+(my2-1)=4m2-2,‎ x1x2=(my1-1)(my2-1)=1.‎ 因为FA=(x1-1,y1),FB=(x2-1,y2),‎ FA‎·FB=(x1-1)(x2-1)+y1y2‎ ‎=x1x2-(x1+x2)+1+4=8-4m2,‎ 故8-4m2=‎8‎‎9‎,解得m=±‎4‎‎3‎.‎ 所以l的方程为3x+4y+3=0,或3x-4y+3=0.‎ 又由①知y2-y1=±‎(4m‎)‎‎2‎-4×4‎=±‎4‎‎3‎‎7‎,‎ 故直线BD的斜率为‎4‎y‎2‎‎-‎y‎1‎=±‎3‎‎7‎,‎ 因而直线BD的方程为3x+‎7‎y-3=0,或3x-‎7‎y-3=0.‎ 因为KF为∠BKD的平分线,故可设圆心M(t,0)(-10)的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,若‎|FM|‎‎|MN|‎=‎5‎‎5‎,则p的值等于(　　)‎ A.‎1‎‎8‎ B.‎1‎‎4‎ C.2 D.4‎ 答案　C　‎ ‎5.(2019届湖北武汉重点中学期初调研,12)已知F是抛物线C:y2=8x的焦点,M是C上一点,FM的延长线交y轴于点N.若M为FN的中点,则|FN|=(　　)‎ A.4 B.6 C.8 D.10‎ 答案　B　‎ ‎6.(2019届广东韶关第一中学9月月考,11)直线l过抛物线y2=ax(a>0)的焦点F且与抛物线交于A,B两点,则‎|AF|·|BF|‎‎|AF|+|BF|‎=(　　)‎ A.a‎2‎ B.a‎4‎ C.2a D.4a 答案　B　‎ ‎7.(2019届广东佛山第一中学9月月考,11)已知P为抛物线y=ax2(a≠0)准线上一点,过点P作抛物线的切线PA,PB,切点分别为A,B.若切线PA的斜率为‎1‎‎3‎,则切线PB的斜率为(　　)‎ A.-a B.-3 C.-‎1‎‎3‎ D.-‎‎1‎a 答案　B　‎ ‎8.(2017江西新余、宜春联考,11)抛物线y2=2px(p>0)的焦点为F,准线为l,A,B是抛物线上的两个动点,且满足∠AFB=‎2π‎3‎,设线段AB的中点M在l上的投影为N,则‎|MN|‎‎|AB|‎的最大值是(　　)‎ A.‎3‎ B.‎3‎‎2‎ C.‎3‎‎3‎ D.‎‎3‎‎4‎ 答案　C　‎ 二、填空题(共5分)‎ ‎9.(2017安徽黄山二模,14)已知抛物线C:y2=8x,焦点为F,点P(0,4),点A在抛物线上,当点A到抛物线准线l的距离与点A到点P的距离之和最小时,延长AF交抛物线于点B,则△AOB的面积为　　　　. ‎ 答案　4‎‎5‎ 三、解答题(共20分)‎ ‎10.(2018广东惠州调研,20)已知圆x2+y2=12与抛物线x2=2py(p>0)相交于A,B两点,点B的横坐标为2‎2‎,F为抛物线的焦点.‎ ‎(1)求抛物线的方程;‎ ‎(2)若过点F且斜率为1的直线l与抛物线和圆交于四个不同的点,从左至右依次为P1,P2,P3,P4,求|P1P2|-|P3P4|的值.‎ 解析　(1)设B(2‎2‎,y0),由题意得‎(2‎2‎‎)‎‎2‎+y‎0‎‎2‎=12,‎‎(2‎2‎‎)‎‎2‎=2py‎0‎,‎ 解之得y‎0‎‎=2,‎p=2,‎所以抛物线的方程为x2=4y.‎ ‎(2)设点P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4),由题意知P1,P3在圆上,P2,P4在抛物线上.因为直线l过点F且斜率为1,所以直线l的方程为y=x+1.‎ 联立y=x+1,‎x‎2‎‎+y‎2‎=12,‎得2x2+2x-11=0,所以x1+x3=-1,x1x3=-‎11‎‎2‎,‎ 所以|P1P3|=‎1+‎‎1‎‎2‎‎(x‎1‎+x‎3‎‎)‎‎2‎-4‎x‎1‎x‎3‎=‎2‎×‎(-1‎)‎‎2‎-4×‎‎-‎‎11‎‎2‎=‎46‎.‎ 由y=x+1,‎x‎2‎‎=4y,‎得x2-4x-4=0,所以x2+x4=4,x2x4=-4.‎ 所以|P2P4|=‎1+‎‎1‎‎2‎‎(x‎2‎+x‎4‎‎)‎‎2‎-4‎x‎2‎x‎4‎=‎2‎×‎4‎‎2‎‎-4×(-4)‎=8.‎ 由题意易知|P1P2|=|P1P3|-|P2P3|①,‎ ‎|P3P4|=|P2P4|-|P2P3|②,‎ ‎①-②得|P1P2|-|P3P4|=|P1P3|-|P2P4|,‎ ‎∴|P1P2|-|P3P4|=‎46‎-8.‎ ‎11.(2019届广东佛山第一中学9月月考,20)已知抛物线C:y2=2px(p>0)的焦点为F,抛物线C上的点M(2,y0)到F的距离为3.‎ ‎(1)求抛物线C的方程;‎ ‎(2)斜率存在的直线l与抛物线相交于相异的两点A(x1,y1),B(x2,y2),且x1+x2=4.若线段AB的垂直平分线交x轴于点G,且GA·GB=5,求直线l的方程.‎ 解析　(1)由抛物线定义知|MF|=2+p‎2‎,‎ 所以2+p‎2‎=3,解得p=2,‎ 所以,抛物线C的方程为y2=4x.‎ ‎(2)设线段AB的中点坐标为(2,m),则y1+y2=2m.‎ 因为直线l的斜率存在,所以m≠0,‎ kAB=y‎2‎‎-‎y‎1‎x‎2‎‎-‎x‎1‎=y‎2‎‎-‎y‎1‎y‎2‎‎2‎‎4‎‎-‎y‎1‎‎2‎‎4‎=‎2‎m,‎ 所以直线AB的方程为y-m=‎2‎m(x-2),即2x-my+m2-4=0.‎ 由‎2x-my+m‎2‎-4=0,‎y‎2‎‎=4x,‎得y2-2my+2m2-8=0,‎ 其中Δ>0,即m2<8,‎y‎1‎‎+y‎2‎=2m①,‎y‎1‎y‎2‎‎=2m‎2‎-8②,‎ 线段AB的垂直平分线方程为y-m=-m‎2‎(x-2),令y=0,得x=4,‎ 所以G(4,0),所以GA=(x1-4,y1),GB=(x2-4,y2).‎ 因为GA·GB=5,所以(x1-4)(x2-4)+y1y2=5,‎ 即x1x2-4(x1+x2)+16+y1y2=5,也即y‎1‎‎2‎y‎2‎‎2‎‎16‎-4×4+16+y1y2=5③,‎ 把②代入③得(m2-4)2+8(m2-4)-20=0,‎ 化简,得(m2+6)(m2-6)=0,‎ 所以m2=6<8,所以m=±‎6‎.‎ 所以直线l的方程为2x-‎6‎y+2=0或2x+‎6‎y+2=0.‎