- 2.24 MB
- 2021-04-18 发布
2018年湖北省高三4月调考
理科数学
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,集合,则( )
A. B. C. D.
2.欧拉公式为虚数单位)是由著名数学家欧拉发明的,她将指数函数定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”.根据欧拉公式,若将表示的复数记为,则的值为( )
A. B. C. D.
3.记不等式组的解集为,若,则实数的最小值是( )
A.0 B.1 C.2 D.4
4.已知,则的值等于( )
A. B. C. D.
5.函数的图像大致为( )
A. B. C. D.
6.已知双曲线的一条渐近线方程为分别是双曲线
的左、右焦点,点在双曲线上,且,则( )
A.1 B.3 C.1或9 D.3或7
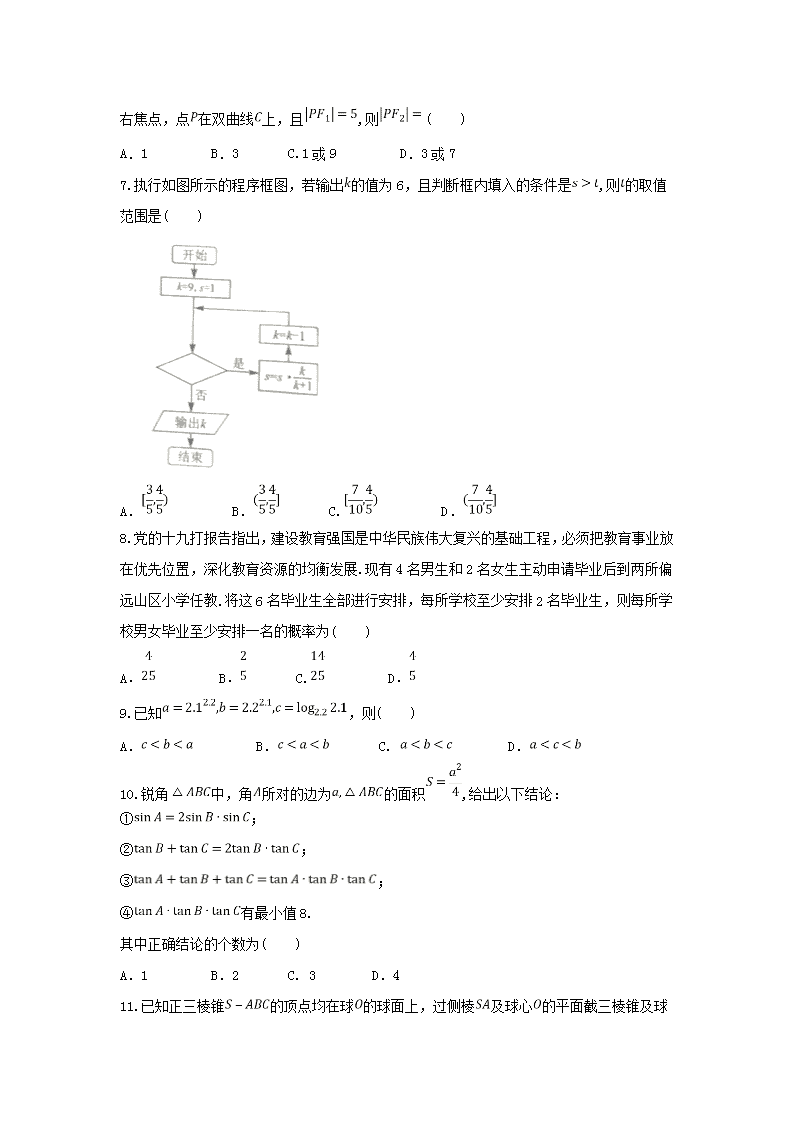
7.执行如图所示的程序框图,若输出的值为6,且判断框内填入的条件是,则的取值范围是( )
A. B. C. D.
8.党的十九打报告指出,建设教育强国是中华民族伟大复兴的基础工程,必须把教育事业放在优先位置,深化教育资源的均衡发展.现有4名男生和2名女生主动申请毕业后到两所偏远山区小学任教.将这6名毕业生全部进行安排,每所学校至少安排2名毕业生,则每所学校男女毕业至少安排一名的概率为( )
A. B. C. D.
9.已知,则( )
A. B. C. D.
10.锐角中,角所对的边为的面积,给出以下结论:
①;
②;
③;
④有最小值8.
其中正确结论的个数为( )
A.1 B.2 C. 3 D.4
11.已知正三棱锥的顶点均在球的球面上,过侧棱及球心
的平面截三棱锥及球面所得截面如图所示,已知三棱锥的体积为,则球的表面积为( )
A. B. C. D.
12.设,其中,则的最小值为( )
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.在的展开式中,常数项为 .(用数字填写答案)
14.已知向量与的夹角为30°,,则的最大值为 .
15.已知函数在区间上恰有三个零点,则的取值范围是 .
16.点是直线上的动点,是圆的两条切线,是切点,则三角形面积的最小值为 .
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. 已知数列,其中,且满足,.
(1)求证:数列为等比数列;
(2)求数列的前项和.
18. 如图,在平行四边形中,°,四边形是矩形,,平面平面.
(1) 若,求证:;
(2) (2)若二面角的正弦值为,求的值.
19.随着网络的飞速发展,人们的生活发生了很大变化,其中无现金支付是一个显著特征,某评估机构对无现金支付的人群进行网络问卷调查,并从参与调查的数万名受访者中随机选取了300人,把这300人分为三类,即使用支付宝用户、使用微信用户、使用银行卡用户,各类用户的人数如图所示,同时把这300人按年龄分为青年人组与中年人组,制成如图所示的列联表:
支付宝用户
非支付宝用户
合计
中老年
90
青年
120
合计
300
(1) 完成列联表,并判断是否有99%的把握认为使用支付宝用户与年龄有关系?
(2)把频率作为概率,从所有无现金支付用户中(人数很多)随机抽取3人,用表示所选3人中使用支付宝用户的人数,求的分布列与数学期望.
附:
0.100
0.050
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
,其中.
20.已知椭圆的离心率为分别为椭圆的左、右焦点,点在椭圆上,当时,内切圆的半径为.
(1)求椭圆的方程;
(2)已知直线与椭圆相较于两点,且,当直线的斜率之和为2时,问:点到直线的距离是否存在最大值?若存在,求出最大值;若不存在,说明理由.
21. 已知函数.
(1)当时,讨论函数的单调性;
(2)求函数的极值.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4-4:坐标系与参数方程
在直角坐标系中,曲线,曲线为参数),以坐标原点为极点,以轴正半轴为极轴,建立极坐标系.
(1)求曲线的极坐标方程;
(2)已知射线与曲线分别交于点(异于原点),当时,求的取值范围.
23.选修4-5:不等式选讲
已知函数的最小值为3.
(1)求的值;
(2)若,求证:.
2018年湖北省高三4月调考
理科数学参考答案
一、选择题
1-5:BACCC 6-10:CCCBD 11、12:AC
二、填空题
13. 112 14. 15. 16.
三、解答题
17.解:(1),
又,所以是首项为4,公比为2的等比数列
(2)由(1)知, ①
又
又,所以为常数数列,) ②
联立①②得:,
所以
18.解:(1)连接,在中,由,由余弦定理易得,又,则;同理由余弦定理易得:,由四边形是矩形,则,又平面平面,所以平面,所以,同理,由勾股定理易求得,,显然,故;
由,所以面,所以,所以面,所以;
(2)以点为原点,所在的直线分别为轴,轴,过点与平面垂直的直线轴建立空间直角坐标系,则
设平面的法向量为,则,即,
取,则,即,
同理可求得平面的法向量为
设二面角的平面角为,则
则,即,解之得或,又,
所以或
19.(1)列联表补充如下
支付宝用户
非支付宝用户
合计
中老年
60
90
150
青年
120
30
150
合计
180
120
300
,
故有99%的把握认为支付宝用户与年龄有关系.
(2)把频率作为概率,从所有无现金支付用户(人数最多)中抽取3人,可以近似看作3次独立重复实验,所以的取值依次为0,1,2,3,且服从二项分布
所以的分布列为
0
1
2
3
20.(1)依题意:,则,即
又,联立解得:,故,所以椭圆的方程为
(2)设,
联立直线和椭圆的方程得:,
当时有:
由得:,即,
整理得:,所以,
化简整理得:,代入得:,
解之得:或,
点到直线的距离,
设,易得或,则,
当时;当时,,
若,则;若,则,当时,
综上所述:,故点到直线的距离没有最大值.
21.解:(1)函数的定义域为,其导数为.当时,
设,则,显然时递增;
时,递减,故,于是,
所以时,递减;时,递增;
(2)由(1)知,
函数在递增,在递减,所以
又当时,,
讨论:
①当时,,此时:
因为时,递增;时,递减;
所以,无极小值;
②当时,,此时:
因为时,递减;时,递增;
所以,无极大值;
③当时,
又在递增,所以在上有唯一零点,且,
易证:时,,所以,
所以
又在递减,所以在上有唯一零点,且,故:
当时,递减;当,递增;
当时,递减;当,递增;
所以,,,
.
22.解:(1)因为,所以曲线的普通方程为:,由,得曲线的极坐标方程,
对于曲线,,则曲线的极坐标方程为
(2)由(1)得,,
因为,则
23.(1)解:
所以,即
(2)由,则原式等价为:,即,
而,
故原不等式成立