- 595.00 KB
- 2021-04-18 发布
高三数学周练22(A)
命题人:曾维平 审题人:辜曦 2017.2.25
一、 选择题:
1.若集合, 集合, 则( )
A. B. C. D.
2.已知是虚数单位, 若, 则( )
A. B. C. D.
3.若, 则( )
A. B. C. D.
4.已知命题, 是简单命题, 则“是真命题”是“是假命题”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分有不必要条件
5. 如图, 四边形是正方形, 延长至, 使得,
若点为的中点, 且, 则( )
A.3 B. C.2 D.1
6.执行下图的程序框图, 则输出的为( )
A.9 B.11 C. 13 D.15
7.从1, 3, 5, 7, 9中任取3个数字, 从2, 4, 6, 8中任取2个数字,
组成没有重复数字的五位数, 则组成的五位数是偶数的概率是( )
A. B. C. D.
8.已知数列满足若对于任意的都
有, 则实数的取值范围是( )
A. B. C. D.
9.已知不等式对于恒成立, 则实数的取值范围是( )
A. B. C. D.
10.如图, 在三棱锥中, 已知三角形和三角形所在平面互相垂直, , , 则直线与平面所角
的大小是( )
A. B. C. D.
11.椭圆的一个焦点为, 该椭圆上有一点, 满足是等边三角形(为坐标原点) , 则椭圆的离心率是( )
A. B. C. D.
12.已知函数与的图象关于轴对称, 当函数和在区间同时递增或同时递减时, 把区间叫做函数的“不动区间”, 若区间为函数的“不动区间”, 则实数的取值范围是( )
A. B. C. D.
一、 填空题
13.二项式的展开式中常数项为 .
14.学校艺术节对同一类的, , , 四项参赛作品, 只评一项一等奖, 在评奖揭晓前, 甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是或作品获得一等奖”;
乙说:“作品获得一等奖”;
丙说:“, 两项作品未获得一等奖”;
丁说:“是作品获得一等奖”.
若这四位同学中只有两位说的话是对的, 则获得一等奖的作品是 .
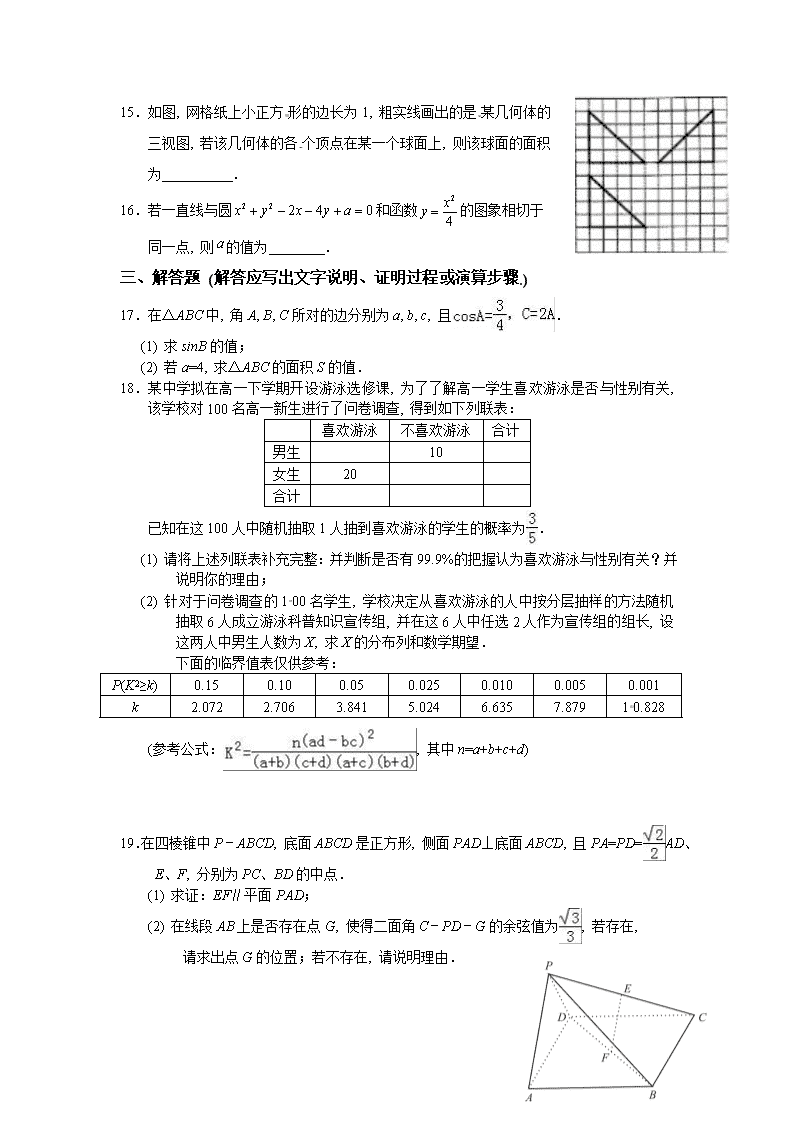
15.如图, 网格纸上小正方形的边长为1, 粗实线画出的是某几何体的
三视图, 若该几何体的各个顶点在某一个球面上, 则该球面的面积
为 .
16.若一直线与圆和函数的图象相切于
同一点, 则的值为 .
三、解答题 (解答应写出文字说明、证明过程或演算步骤.)
17.在△ABC中, 角A, B, C所对的边分别为a, b, c, 且.
(1) 求sinB的值;
(2) 若a=4, 求△ABC的面积S的值.
18.某中学拟在高一下学期开设游泳选修课, 为了了解高一学生喜欢游泳是否与性别有关, 该学校对100名高一新生进行了问卷调查, 得到如下列联表:
喜欢游泳
不喜欢游泳
合计
男生
10
女生
20
合计
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为.
(1) 请将上述列联表补充完整:并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(2) 针对于问卷调查的100名学生, 学校决定从喜欢游泳的人中按分层抽样的方法随机抽取6人成立游泳科普知识宣传组, 并在这6人中任选2人作为宣传组的组长, 设这两人中男生人数为X, 求X的分布列和数学期望.
下面的临界值表仅供参考:
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:, 其中n=a+b+c+d)
19.在四棱锥中P﹣ABCD, 底面ABCD是正方形, 侧面PAD⊥底面ABCD, 且PA=PD=AD、E、F, 分别为PC、BD的中点.
(1) 求证:EF∥平面PAD;
(2) 在线段AB上是否存在点G, 使得二面角C﹣PD﹣G的余弦值为, 若存在,
请求出点G的位置;若不存在, 请说明理由.
20.已知椭圆C:的短轴长为2, 离心率e=,
(1) 求椭圆C的标准方程:
(2) 若F1、F2分别是椭圆C的左、右焦点, 过F2的直线l与椭圆C交于不同的两点A、B,
求△F1AB的内切圆半径的最大值.
21.已知函数(为自然对数的底数), 是的导函数.
(Ⅰ)当时, 求证;
(Ⅱ)是否存在正整数, 使得对一切恒成立?若存在, 求出的最大值;若不存在, 说明理由.
请考生在第22、23题中任选一题作答, 如果多做, 则按所做的第一题记分.作答时请写清题号.[选修4-4:坐标系与参数方程]
22.已知在直角坐标系中, 曲线的C参数方程为(φ为参数) , 现以原点为极点, x轴的正半轴为极轴建立极坐标系, 直线l的极坐标方程为ρ=.[来源:学科网]
(1) 求曲线C的普通方程和直线l的直角坐标方程;
(2) 在曲线C上是否存在一点P, 使点P到直线l的距离最小?若存在, 求出距离的最小值及
点P的直角坐标;若不存在, 请说明理由.
[选修4-5:不等式选讲][来源:Z|xx|k.Com]
23.已知函数f(x) =|x|+|x﹣3|.
(1) 解关于x的不等式f(x) ﹣5≥x;
(2) 设m, n∈{y|y=f(x) }, 试比较mn+4与2(m+n) 的大小.
高三数学周练22(A)
参考答案
一、ABB CDBBB AC
二、13、24 14、B 15、 16、3
三、17、解:(1)∵由得, …
∴cosC=cos2A=cos2A﹣sin2A=, …2分
∴sinC==, …3分
又∵A+B+C=π, sinB=sin[π﹣(A+C)]=sin(A+C), …4分
∴.…
(2)由正弦定理得, …
∴△ABC的面积.…
18.解:(1)因为在100人中随机抽取1人抽到喜欢游泳的学生的概率为,
所以喜欢游泳的学生人数为人…
其中女生有20人, 则男生有40人, 列联表补充如下:
喜欢游泳
不喜欢游泳
合计
男生
40
10
50
女生
20
30
50
合计
60
40
100
…
因为…
所以有99.9%的把握认为喜欢游泳与性别有关…
(2)喜欢游泳的共60人, 按分层抽样抽取6人, 则每个个体被抽到的概率均为,
从而需抽取男生4人, 女生2人.
故X的所有可能取值为0, 1,
2…,
X的分布列为:[来源:学#科#网Z#X#X#K]
X
0
1
2
P
…
…
19.(1)证明:连接AC, 由正方形性质可知, AC与BD相交于点F,
所以, 在△PAC中, EF∥PA…
又PA⊂平面PAD, EF⊄平面PAD…
所以EF∥平面PAD…
(2)取AD的中点O, 连接OP, OF,
因为PA=PD, 所以PO⊥AD,
又因为侧面PAD⊥底面ABCD, 交线为AD, 所以PO⊥平面ABCD,
以O为原点, 分别以射线OA, OF和OP为x轴, y轴和z轴建立空间直角坐标系, O﹣xyz, 不妨设AD=2…
则有P(0, 0, 1), D(﹣1, 0, 0), C(﹣1, 2, 0), 假设在AB上存在点G(1, a, 0), 0<a<2,
则=(﹣1, 2, ﹣1), =(﹣1, 0, ﹣1), =(2, a, 0)…
因为侧面PAD⊥底面ABCD, 交线为AD, 且底面是正方形,
所以CD⊥平面PAD, 则CD⊥PA,
由PA2+PD2=AD2得PD⊥PA,
所以PA⊥PDC, 即平面PDC的一个法向量为=(1, 0, ﹣1)…
设平面PDG的法向量为=(x, y, z), 则, 亦即, 可取=(a, ﹣2, ﹣a)…
由二面角C﹣PD﹣G的余弦值为, 可得a=1…,
所以线段AB上存在点G, 且G为AB的中点,
使得二面角C﹣PD﹣G的余弦值为…
20.解:(1)由题意可得…
解得…
故椭圆的标准方程为…
(2)设A(x1, y1), B(x2, y2), 设△F1AB的内切圆的半径为R,
因为△F1AB的周长为4a=8, ,
因此最大, R就最大…,
由题意知, 直线l的斜率不为零, 可设直线l的方程为x=my+1,
由得(3m2+4)y2+6my﹣9=0, [来源:学+科+网]
所以, …
又因直线l与椭圆C交于不同的两点,
故△>0, 即(6m)2+36(3m2+4)>0, m∈R, 则
…
令, 则t≥1, .
令, 由函数的性质可知, 函数f(t)在上是单调递增函数,
即当t≥1时, f(t)在[1, +∞)上单调递增,
因此有, 所以,
即当t=1, m=0时, 最大, 此时,
故当直线l的方程为x=1时, △F1AB内切圆半径的最大值为…
21.解:(Ⅰ)当时, , 则 ,
令, 则 ,
令, 得, 故在时取得最小值,
在上为增函数,
,
(Ⅱ) ,
由, 得对一切恒成立,
当时, 可得, 所以若存在, 则正整数的值只能取1,2.
下面证明当时, 不等式恒成立,
设 , 则 ,
由(Ⅰ) , ,
当时, ;当时, ,
即在上是减函数, 在上是增函数,
,
当时, 不等式恒成立
所以的最大值是2.
22.解:(1)曲线的C参数方程为(φ为参数), 普通方程为(x﹣1)2+(y﹣1)2=4,
直线l的极坐标方程为ρ=, 直角坐标方程为x﹣y﹣4=0;
(2)点P到直线l的距离d==
∴φ﹣=2kπ﹣, 即φ=2kπ﹣(k∈Z), 距离的最小值为, 点P的直角坐标(3, -1).
23.解:(1)…
得或或, 解之得或x∈ϕ或x≥8,
所以不等式的解集为…
(2)由(1)易知f(x)≥3, 所以m≥3, n≥3…
由于2(m+n)﹣(mn+4)=2m﹣mn+2n﹣4=(m﹣2)(2﹣n)…
且m≥3, n≥3, 所以m﹣2>0, 2﹣n<0, 即(m﹣2)(2﹣n)<0,
所以2(m+n)<mn+4…