- 863.50 KB
- 2021-04-18 发布
北京市朝阳区2017-2018学年度第一学期高三年级期中统一考试
数学试卷(理工类) 2017.11
(考试时间120分钟 满分150分)
本试卷分为选择题(共40分)和非选择题(共110分)两部分
第一部分(选择题 共40分)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.
1. 已知集合,,则
A. B. C. D.
2. 已知实数满足条件则的最大值为
A. 12 B. 10 C. 8 D. 6
3.要得到函数的图象,只需将函数的图象上所有的点
A. 先向右平移个单位长度,再将横坐标伸长为原来的倍,纵坐标不变
B. 先向右平移个单位长度,横坐标缩短为原来的倍,纵坐标不变
C. 横坐标缩短为原来的倍,纵坐标不变,再向右平移个单位长度
D. 横坐标变伸长原来的倍,纵坐标不变,再向右平移个单位长度
4. 已知非零平面向量,则“”是“存在非零实数,使”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.已知是等差数列( )的前项和,且,以下有四个命题:
①数列中的最大项为 ②数列的公差
③ ④
其中正确的序号是( )
A. ②③ B. ②③④ C. ②④ D. ①③④
6. 如图,在直角梯形中,,,是的中点,,则
A. B. C. D.
(
7. 袋子里有编号为的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,再让甲、乙分别推断这两个球的编号.
甲说:“我无法确定.”
乙说:“我也无法确定.”
甲听完乙的回答以后,甲说:“我现在可以确定两个球的编号了.”
根据以上信息, 你可以推断出抽取的两球中
A.一定有3号球 B.一定没有3号球 C.可能有5号球 D.可能有6号球
8. 已知函数与函数在区间都为减函数,设,且,,,则的大小关系是( )
A. B. C. D.
第二部分(非选择题 共110分)
二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.
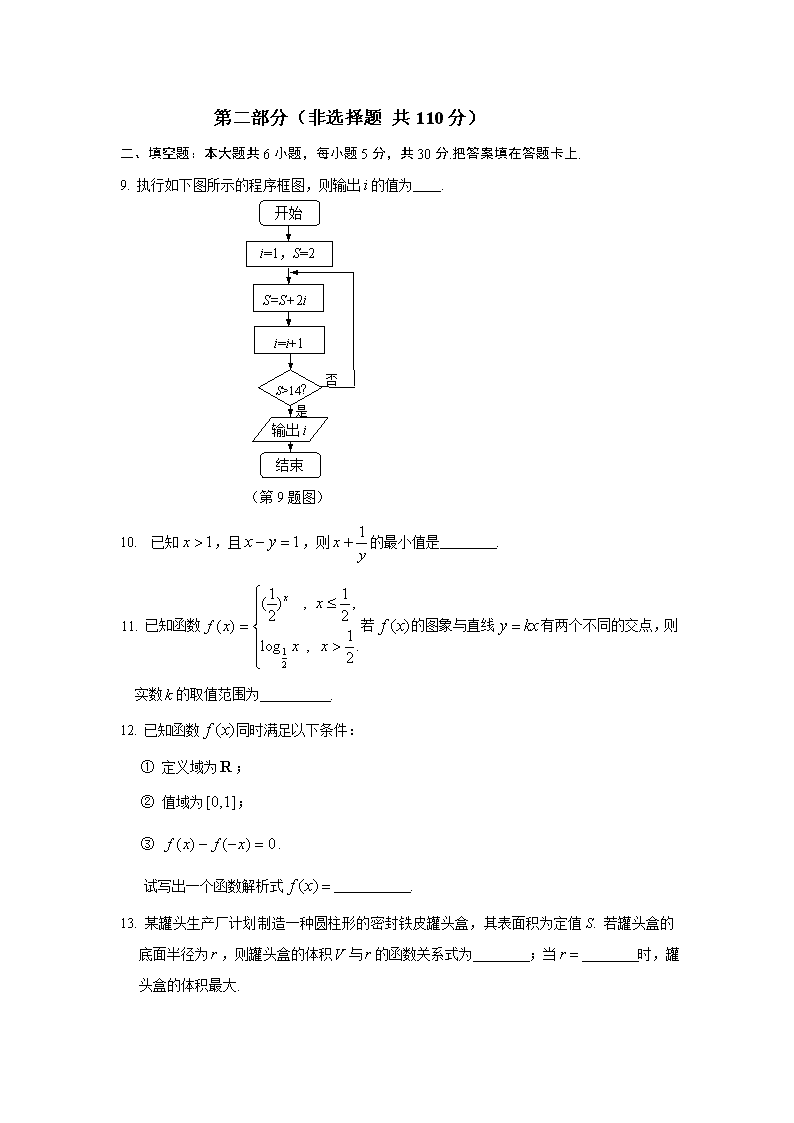
9. 执行如下图所示的程序框图,则输出的值为 .
开始
i=1,S=2
结束
i=i+1
S>14?
输出i
是
否
S=S+2i
(第9题图)
10. 已知,且,则的最小值是 .
11. 已知函数若的图象与直线有两个不同的交点,则实数的取值范围为 .
12. 已知函数同时满足以下条件:
① 定义域为;
② 值域为;
③ .
试写出一个函数解析式 .
13. 某罐头生产厂计划制造一种圆柱形的密封铁皮罐头盒,其表面积为定值S. 若罐头盒的底面半径为,则罐头盒的体积与的函数关系式为 ;当 时,罐头盒的体积最大.
14. 将集合表示为它的5个三元子集(三元集:含三个元素的集合)的并集,并且这些三元子集的元素之和都相等,则每个三元集的元素之和为 ;请写出满足上述条件的集合的5个三元子集 . (只写出一组)
三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.
15. (本小题满分13分)
已知数列的前项和为( ),满足.
(Ⅰ)求数列的通项公式;
(Ⅱ)若数列满足,求数列的前项和.
16. (本小题满分13分)
已知函数.
(Ⅰ)求函数的最小正周期;
(Ⅱ)当时,求函数的取值范围.
17. (本小题满分13分)
在中,,.
(Ⅰ)试求的值;
(Ⅱ)若,试求的面积.
18. (本小题满分14分)
已知函数,.
(Ⅰ)求函数的单调区间;
(Ⅱ)设,其中为函数的导函数.判断在定义域内是否为单调函数,并说明理由.
19. (本小题满分14分)
已知函数.
(Ⅰ)求曲线在点处的切线方程;
(Ⅱ)求证:;
(Ⅲ)判断曲线是否位于轴下方,并说明理由.
20. (本小题满分13分)
数列是正整数的任一排列,且同时满足以下两个条件:
①;②当时,().
记这样的数列个数为.
(I)写出的值;
(II)证明不能被4整除.
北京市朝阳区2017-2018学年度第一学期高三年级期中统一考试
数学答案(理工类)2017.11
一、 选择题:
题号
1
2
3
4
5
6
7
8
答案
C
B
C
A
B
D
D
C
二、 填空题:
9. 5 10. 3 11.
12. 或或(答案不唯一)
13. ;
14. 24;, ,,,(答案不唯一)
三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.
15. (本小题满分13分)
解:(Ⅰ)当时,.
当时,,
,即
所以数列是首项为1,公比为2的等比数列.
故, . ┈┈ 8分
(Ⅱ)由已知得.
因为,
所以是首项为0,公差为的等差数列.
故的前项和. ┈┈ 13分
16. (本小题满分13分)
解:因为,
所以
.
(Ⅰ)函数的最小正周期为. ┈┈ 8分
(Ⅱ)因为,所以.
所以.
所以. ┈┈ 13分
17. (本小题满分13分)
解:(Ⅰ)因为,,所以.
所以.
所以.
所以.
所以.
所以. ┈┈ 7分
(Ⅱ)因为,,,由余弦定理得
.
所以,.
所以△的面积. ┈┈ 13分
18. (本小题满分14分)
解:(Ⅰ)函数的定义域为..
① 当时,令,解得:或,为减函数;
令,解得:,为增函数.
② 当时,恒成立,函数为减函数;
③ 当时,令,解得:或,函数为减函数;
令,解得:,函数为增函数.
综上,
当时,的单调递减区间为;单调递增区间为;
当时, 的单调递减区间为 ;
当时,的单调递减区间为;单调递增区间为.
┈┈ 8分
(Ⅱ)在定义域内不为单调函数,以下说明:
.
记,则函数为开口向上的二次函数.
方程的判别式 恒成立.
所以,有正有负. 从而有正有负.
故在定义域内不为单调函数. ┈┈ 14分
19. (本小题满分14分)
解:函数的定义域为,
(Ⅰ),又,
曲线在处的切线方程为
.
即. ┈┈ 4分
(Ⅱ)“要证明”等价于“”.
设函数.
令,解得.
因此,函数的最小值为.故.
即. ┈┈ 9分
(Ⅲ)曲线位于轴下方. 理由如下:
由(Ⅱ)可知,所以.
设,则.
令得;令得.
所以在上为增函数,上为减函数.
所以当时,恒成立,当且仅当时,.
又因为, 所以恒成立.
故曲线位于轴下方. ┈┈ 14分
20. (本小题满分13分)
(Ⅰ)解:. ┈┈ 3分
(Ⅱ)证明:把满足条件①②的数列称为项的首项最小数列.
对于个数的首项最小数列,由于,故或3.
(1)若,则构成项的首项最小数列,其个数为;
(2)若,则必有,故构成项的首项最小数列,其个数为;
(3)若则或. 设是这数列中第一个出现的偶数,则前项应该是,是或,即与是相邻整数.
由条件②,这数列在后的各项要么都小于它,要么都大于它,因为2在之后,故后的各项都小于它.
这种情况的数列只有一个,即先排递增的奇数,后排递减的偶数.
综上,有递推关系:,.
由此递推关系和(I)可得,各数被4除的余数依次为:
1,1,2,0,2,1,2,1,3,2,0,0,3,0,1,1,2,0,…
它们构成14为周期的数列,又,
所以被4除的余数与被4除的余数相同,都是1,
故不能被4整除. ┈┈ 13分