2018届二轮复习空间中的平行与垂直的证明问题课件（全国通用） 31页

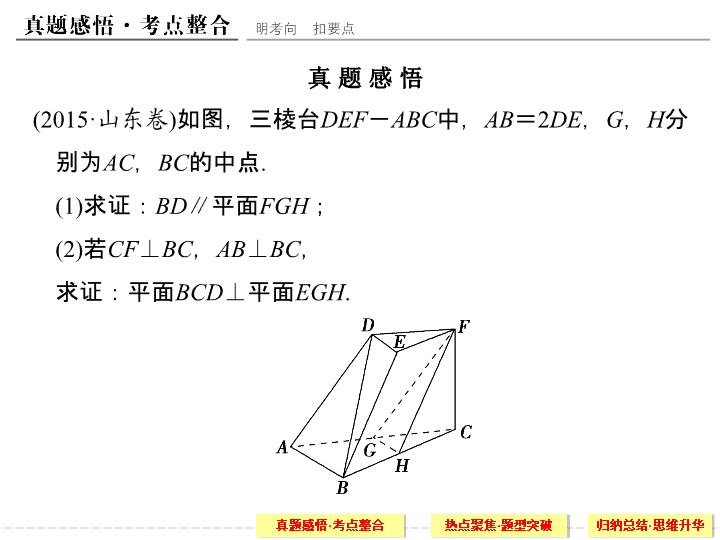
第 2 讲　 空间中的平行与垂直的证明问题 高考定位 　 空间中的平行与垂直的证明每年必考，主要以解答题形式出现，属中等难度题 . 真 题 感 悟 (2015· 山东卷 ) 如图，三棱台 DEF － ABC 中， AB ＝ 2 DE ， G ， H 分别为 AC ， BC 的中点 . (1) 求证： BD ∥ 平面 FGH ； (2) 若 CF ⊥ BC ， AB ⊥ BC ， 求证：平面 BCD ⊥ 平面 EGH . 证明　 (1) 法一 　连接 DG ， CD ，设 CD ∩ GF ＝ M ，连接 MH . 在三棱台 DEF － ABC 中， AB ＝ 2 DE ， G 为 AC 的中点， 可得 DF ∥ GC ， DF ＝ GC ， 所以四边形 DFCG 为平行四边形 . 则 M 为 CD 的中点， 又 H 为 BC 的中点， 所以 HM ∥ BD ， 又 HM ⊂ 平面 FGH ， BD ⊄ 平面 FGH ， 所以 BD ∥ 平面 FGH . 法二　 在三棱台 DEF － ABC 中，由 BC ＝ 2 EF ， H 为 BC 的中点， 可得 BH ∥ EF ， BH ＝ EF ， 所以四边形 HBEF 为平行四边形， 可得 BE ∥ HF . 在 △ ABC 中， G 为 AC 的中点， H 为 BC 的中点，所以 GH ∥ AB . 又 GH ∩ HF ＝ H ， 所以平面 FGH ∥ 平面 ABED . 又因为 BD ⊂ 平面 ABED ， 所以 BD ∥ 平面 FGH . (2) 连接 HE ， GE ，因为 G ， H 分别为 AC ， BC 的中点， 所以 GH ∥ AB . 由 AB ⊥ BC ，得 GH ⊥ BC . 又 H 为 BC 的中点， 所以 EF ∥ HC ， EF ＝ HC ， 因此四边形 EFCH 是平行四边形， 所以 CF ∥ HE . 又 CF ⊥ BC ， 所以 HE ⊥ BC . 又 HE ， GH ⊂ 平面 EGH ， HE ∩ GH ＝ H ， 所以 BC ⊥ 平面 EGH . 又 BC ⊂ 平面 BCD ， 所以平面 BCD ⊥ 平面 EGH . 考 点 整 合 1. 直线、平面平行的判定及其性质 (1) 线面平行的判定定理： a ⊄ α ， b ⊂ α ， a ∥ b ⇒ a ∥ α . (2) 线面平行的性质定理： a ∥ α ， a ⊂ β ， α ∩ β ＝ b ⇒ a ∥ b . (3) 面面平行的判定定理： a ⊂ β ， b ⊂ β ， a ∩ b ＝ P ， a ∥ α ， b ∥ α ⇒ α ∥ β . (4) 面面平行的性质定理： α ∥ β ， α ∩ γ ＝ a ， β ∩ γ ＝ b ⇒ a ∥ b . 2. 直线、平面垂直的判定及其性质 (1) 线面垂直的判定定理： m ⊂ α ， n ⊂ α ， m ∩ n ＝ P ， l ⊥ m ， l ⊥ n ⇒ l ⊥ α . (2) 线面垂直的性质定理： a ⊥ α ， b ⊥ α ⇒ a ∥ b . (3) 面面垂直的判定定理： a ⊂ β ， a ⊥ α ⇒ α ⊥ β . (4) 面面垂直的性质定理： α ⊥ β ， α ∩ β ＝ l ， a ⊂ α ， a ⊥ l ⇒ a ⊥ β . 热点一　以棱柱、棱锥为载体的平行、垂直关系的证明 证明　 (1) 由题意知， E 为 B 1 C 的中点， 又 D 为 AB 1 的中点， 因此 DE ∥ AC . 又因为 DE ⊄ 平面 AA 1 C 1 C ， AC ⊂ 平面 AA 1 C 1 C ， 所以 DE ∥ 平面 AA 1 C 1 C . (2) 因为棱柱 ABC － A 1 B 1 C 1 是直三棱柱， 所以 CC 1 ⊥ 平面 ABC . 因为 AC ⊂ 平面 ABC ， 所以 AC ⊥ CC 1 . 又因为 AC ⊥ BC ， CC 1 ⊂ 平面 BCC 1 B 1 ， BC ⊂ 平面 BCC 1 B 1 ， BC ∩ CC 1 ＝ C ， 所以 AC ⊥ 平面 BCC 1 B 1 . 又因为 BC 1 ⊂ 平面 BCC 1 B 1 ， 所以 BC 1 ⊥ AC . 因为 BC ＝ CC 1 ，所以矩形 BCC 1 B 1 是正方形， 因此 BC 1 ⊥ B 1 C . 因为 AC ， B 1 C ⊂ 平面 B 1 AC ， AC ∩ B 1 C ＝ C ，所以 BC 1 ⊥ 平面 B 1 AC . 又因为 AB 1 ⊂ 平面 B 1 AC ， 所以 BC 1 ⊥ AB 1 . 探究提高 　 垂直、平行关系证明中应用转化与化归思想的常见类型 . (1) 证明线面、面面平行，需转化为证明线线平行 . (2) 证明线面垂直，需转化为证明线线垂直 . (3) 证明线线垂直，需转化为证明线面垂直 . (4) 证明面面垂直，需转化为证明线面垂直，进而转化为证明线线垂直 . 证明 　 (1) 法一 　如图 1 ，取 PA 的中点 H ，连接 EH ， DH . 又因为 E 为 PB 的中点， 所以 EH ∥ AB ， EH ＝ AB . 又 AB ∥ CD ， CD ＝ AB ， 所以 EH ∥ CD ， EH ＝ CD . 所以四边形 DCEH 是平行四边形 . 所以 CE ∥ DH . 又 DH ⊂ 平面 PAD ， CE ⊄ 平面 PAD ， 所以 CE ∥ 平面 PAD . 又 DH ⊂ 平面 PAD ， CE ⊄ 平面 PAD ， 所以 CE ∥ 平面 PAD . 因为 E ， F 分别为 PB ， AB 的中点， 所以 EF ∥ PA . 又 EF ⊄ 平面 PAD ， PA ⊂ 平面 PAD ， 所以 EF ∥ 平面 PAD . 因为 CF ∩ EF ＝ F ， 故平面 CEF ∥ 平面 PAD . 又 CE ⊂ 平面 CEF ， 所以 CE ∥ 平面 PAD . (2) 因为 E ， F 分别为 PB ， AB 的中点， 所以 EF ∥ PA . 又 AB ⊥ PA ，所以 AB ⊥ EF . 同理可证 AB ⊥ FG . 又 EF ∩ FG ＝ F ， EF ⊂ 平面 EFG ， FG ⊂ 平面 EFG ， 因此 AB ⊥ 平面 EFG . 又 M ， N 分别为 PD ， PC 的中点， 所以 MN ∥ DC . 又 AB ∥ DC ， 所以 MN ∥ AB ， 所以 MN ⊥ 平面 EFG . 又 MN ⊂ 平面 EMN ， 所以平面 EFG ⊥ 平面 EMN . 热点二　利用平行、垂直关系判断点的存在性 探究提高 　 探求点的位置常常是线段的中点、三等分点等，关键是通过垂直、平行关系寻找线线平行转化为线段成比例 . (1) 证明　 因为四边形 ABB 1 A 1 和 ACC 1 A 1 都是矩形， 所以 AA 1 ⊥ AB ， AA 1 ⊥ AC . 因为 AB ， AC 为平面 ABC 内两条相交的直线， 所以 AA 1 ⊥ 平面 ABC . 因为直线 BC ⊂ 平面 ABC ，所以 AA 1 ⊥ BC . 又由已知， AC ⊥ BC ， AA 1 ， AC 为平面 ACC 1 A 1 内两条相交的直线， 所以 BC ⊥ 平面 ACC 1 A 1 . 连接 OM ，从而四边形 MDEO 为平行四边形， 则 DE ∥ MO . 因为直线 DE ⊄ 平面 A 1 MC ， MO ⊂ 平面 A 1 MC ， 所以直线 DE ∥ 平面 A 1 MC . 即线段 AB 上存在一点 M ( 线段 AB 的中点 ) ， 使直线 DE ∥ 平面 A 1 MC . 热点三　图形翻折中的平行、垂直关系 探究提高 　 (1) 解决折叠问题的关键是搞清翻折前后哪些位置关系和数量关系改变，哪些不变，抓住翻折前后不变的量，充分利用原平面图形的信息是解决问题的突破口 .(2) 把平面图形翻折后，经过恰当连线就能得到三棱锥、四棱锥，从而把问题转化到我们熟悉的几何体中解决 . 1. 空间中点、线、面的位置关系的判定 (1) 可以从线、面的概念、定理出发，学会找特例、反例 . 　 (2) 可以借助长方体，在理解空间点、线、面位置关系的基础上，抽象出空间线、面的位置关系的定义 . 2. 垂直、平行关系的基础是线线垂直和线线平行，常用方法如下： 　(1) 证明线线平行常用的方法：一是利用平行公理，即证两直线同时和第三条直线平行；二是利用平行四边形进行平行转换：三是利用三角形的中位线定理证线线平行；四是利用线面平行、面面平行的性质定理进行平行转换 . (2) 证明线线垂直常用的方法： ① 利用等腰三角形底边中线即高线的性质； ② 勾股定理； ③ 线面垂直的性质：即要证两线垂直，只需证明一线垂直于另一线所在的平面即可， l ⊥ α ， a ⊂ α ⇒ l ⊥ a . 3. 在应用直线和平面平行的性质定理时，要防止出现 “ 一条直线平行于一个平面就平行于这个平面内的所有直线 ” 的错误 . 4. 解决平面图形的翻折问题，关键是抓住平面图形翻折前后的不变 “ 性 ” 与 “ 量 ” ，即两条直线的平行与垂直关系以及相关线段的长度、角度等 .