- 1.95 MB
- 2021-04-18 发布
广东惠来一中高二理数试题
本试卷分第Ⅰ卷和第Ⅱ卷两部分,全卷满分150分,考试时间120分钟。
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在空间直角坐标系中,点关于平面对称的点的坐标为( )
A. B. C. D.
2.集合,,则( )
A. B. C. D.
3.已知,则( )
A. B. C. D.
4.当时,的最小值为( )
A.9 B.10 C.12 D.13
5.已知关于的方程为,若,则方程有实数根的概率为( )
A. B. C. D.
6.在△ABC中,BC=2,B=,当△ABC的面积等于时,AB= ( )
A. B. C. D.
7.若“”是“函数的图象不过第三象限”的必要不充分条件,则实数能取的最大整数为( )
A. 1 B. 0 C. -2 D.-1
8.已知动点M到椭圆左焦点的距离比到其右焦点的距离大2,则动点M的轨迹方程是( )
A. B.
C. D.
9.已知实数满足,则=的最大值与最小值之差为( )
A. B. C. D.
10.已知为定义在实数集R上的奇函数,且在区间(0,+∞)上是增函数,又=0,则不等式的解集是( )
A. B.
C. D.
11.已知函数=(,,)的最大值为2,周期为,将函数=图象向右平移个单位得到函数=的图象,若函数=是偶函数,则函数的一条对称轴为( )
A. B. C. D.
12.已知函数的定义域的R,当时,,且对任意的实数,等式
成立,若数列{an}满足,且,则下
列结论成立的是( )
A. B.
C. D.
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分。
13.若命题:“存在,使成立”为假命题,则实数的取值范围为 .
14.已知坐标原点到直线()的距离为,点在以点为圆心的圆上,则圆的最大半径是 .
1 15.直线与抛物线交于两点,为坐标原点,若直线的斜率, 满足
,则直线过定点 .
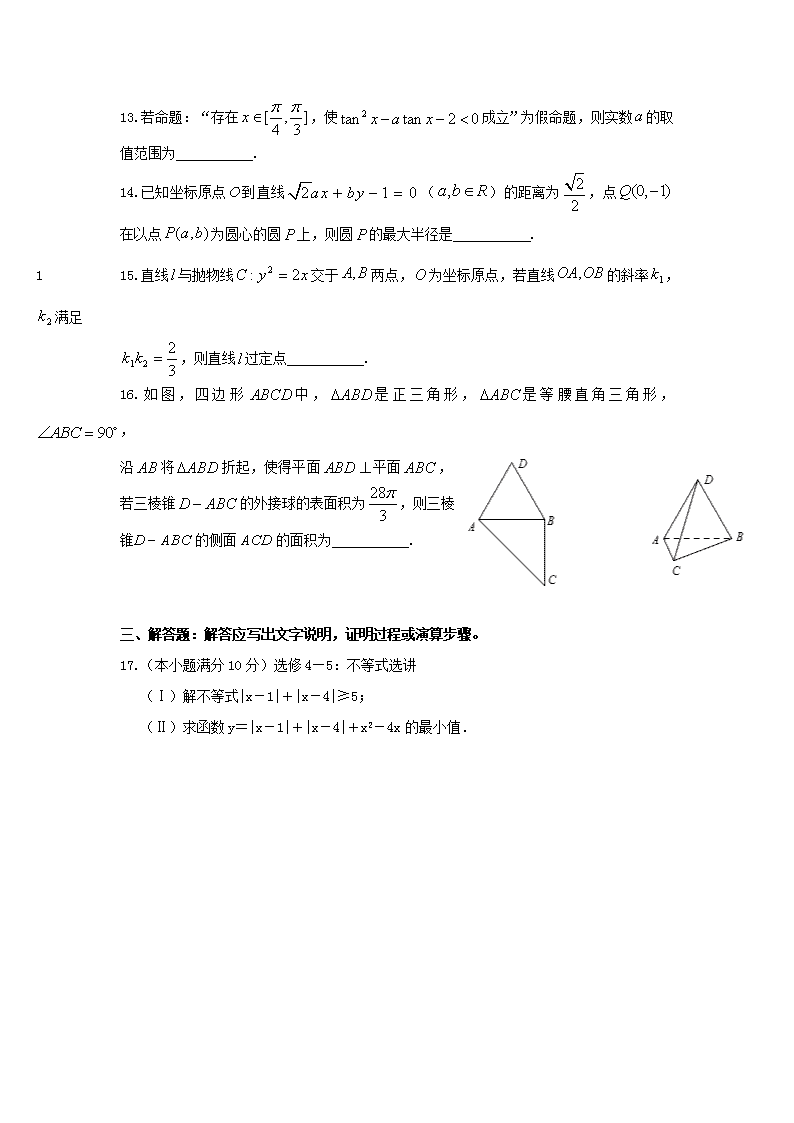
16.如图,四边形中,是正三角形,是等腰直角三角形,,
沿将折起,使得平面平面,若三棱锥的外接球的表面积为,则三棱锥的侧面的面积为 .
三、解答题:解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分10分)选修4—5:不等式选讲
(Ⅰ)解不等式|x-1|+|x-4|≥5;
(Ⅱ)求函数y=|x-1|+|x-4|+x2-4x的最小值.
18.(本小题满分12分)
在中,角、、的对边分别为、、,且.
(Ⅰ)求角的值;
(Ⅱ)若,边上的中线,求AB.
19.(本小题满分12分)
已知数列{}的各项均不为0,,且满足,数列满足.
(Ⅰ)求证:数列为等比数列;
(Ⅱ)若,求数列的前项和.
20.(本小题满分12分)
如图,是平行四边形,已知,,平面平面.
(Ⅰ)证明:;
(Ⅱ)若,求平面与平面所成二面角的余弦值.
21.(本小题满分12分)
已知椭圆的焦距为4,设右焦点为,过原点的直线与椭圆交于两点,线段的中点为,线段的中点为,且.
(Ⅰ)求弦的长;
(Ⅱ) 若直线的斜率为, 且, 求椭圆的长轴长的取值范围.
22.(本小题满分12分)
已知f(x)=loga是奇函数(其中a>1).
(Ⅰ)求实数m的值;
(Ⅱ)判断f(x)在区间(2,+∞)内的单调性,并证明;
(Ⅲ)当x∈(r,a﹣2)时,f(x)的值域恰为(1,+∞),求实数a与r的值.
参考答案及评分标准
一、选择题
1.A 2.B 3.D 4.A 5.B 6.D 7.D 8.C 9.B 10.D 11. C 12.D
二、填空题
13. 14. 15. 16.
三、解答题
17.解:(Ⅰ)当x<1时,1-x+4-x≥5,得x≤0,此时x≤0;
当1≤x≤4时,x-1+4-x≥5,得3≥5,此时x∈∅;
当x>4时,x-1+x-4≥5,得x≥5,此时x≥5.
综上所述,原不等式的解集是(-∞,0]∪[5,+∞). …………5分
(Ⅱ)因为|x-1|+|x-4|≥|(x-1)-(x-4)|=3,
当且仅当1≤x≤4时取等号;
x2-4x=(x-2)2-4≥-4,当且仅当x=2时取等号.
故|x-1|+|x-4|+x2-4x≥3-4=-1,当x=2时取等号.
所以y=|x-1|+|x-4|+x2-4x的最小值为-1. …………10分
18.解:(Ⅰ)因为,
所以,由正弦定理,得, ………………………2分
即,
因为,所以, ………………………5分
因为为三角形内角,所以. ………………………6分
(Ⅱ)在中,,,,
由余弦定理,得,
即, ………………………8分
解得(舍去), ………………………10分
在中,由余弦定理,得,
所以. ………………………12分
19.解:(Ⅰ)∵,,∴,………………1分
即,,
∵,∴,∴,
∴数列是首项为3,公比为3的等比数列.………………4分
(Ⅱ)由(Ⅰ)知,=,∴=,
∴, ┄5分
∴数列{}的通项公式; ………………6分
=,┄7分
∴=
=,………………8分
设=,①
∴=②
①-②得,===,
∴=,………………………………10分
∵=, ………………11分
∴=.………………12分
20.解:(Ⅰ)∵是平行四边形,且
∴,∴,即 ,
取BC的中点F,连接EF,∵,∴ , ………………2分
又∵平面平面,平面平面,∴平面,
∵平面,∴ ,
∵平面,∴平面,
∵平面,∴ . ……………………………… 6分
(Ⅱ)∵,由(Ⅰ)得 .
以B为坐标原点,所在直线分别为轴,以过点B且与FE平行的直线为z轴建立空间直角坐标系(如图),
则,
∴……………… 8分
设平面的一个法向量为,则
,即 ,
得平面的一个法向量为,
由(Ⅰ)知平面,∴可设平面的一个法向量为,……………… 11分
设平面与平面所成二面角为,
则 ,
即平面与平面所成二面角的余弦值为.……………… 12分
21.解:(Ⅰ)设,……………2分
则
所以的长为 .……………………………5分
(Ⅱ)设方程为,和椭圆方程联立消元整理得…………………7分
又,则, …………10分
则,长轴长的取值范围是 .……………………12分
22.解:(Ⅰ)因为f(x)是奇函数,则f(﹣x)+f(x)=0,
即loga+loga=0,
所以,解得m=±1. ………………………………2分
当m=﹣1时,f(x)无意义.
故m的值为1. ………………………………3分
(Ⅱ)函数f(x)在区间(2,+∞)内单调递减.
由(Ⅰ)得,.
设2<x1<x2,
则f(x2)﹣f(x1)=﹣=.………4分
因为2<x1<x2,
所以0<x1x2+2(x1﹣x2)﹣4<x1x2﹣2(x1﹣x2)﹣4,
因为a>1,所以f(x2)<f(x1).
所以函数f(x)在区间(2,+∞)内单调递减. ………………………………7分
(Ⅲ)由(Ⅰ)得,.
由,得函数f(x)的定义域为(﹣∞,﹣2)∪(2,+∞).
又因为,所以f(x)∈(﹣∞,0)∪(0,+∞). ………………………………8分
令f(x)=1,则=a,解得.
所以f()=1. ………………………………9分
当a>1时,>2,此时f(x)在区间(2,+∞)内单调递减.
所以当x∈(2,)时,f(x)∈(1,+∞). ………………………………10分
由题意,得r=2,a﹣2=,解得a=5.
所以当x∈(r,a﹣2),f(x)的值域恰为(1,+∞)时,a和r的值分别为5和2.………12分