2020届二轮复习解三角形学案（全国通用） 49页

解三角形 ​ 一般地，把三角形的三个角 ， ， 和它们的对边 ， ， 叫做三角形的元素．已知三角 形的几个元素求其他元素的过程叫做解三角形． 正弦定理 正弦定理（law of sines）在一个三角形中，各边的长和它所对角正弦的比相等，即 sin sin sin ㄍ㌰ （ ㌰ 为三角形外接圆半径）． 一般地，我们把三角形的三个角及其对边分别叫做三角形的元素．已知三角形的几个元素求其 他元素的过程叫做解三角形． 余弦定理 余弦定理（law of cosines）三角形任何一边的平方等于其他两边的平方和减去这两边与它们夹 角的余弦值的积的两倍，即 ​ ㄍ ㄍ ㄍ ㄍcos ㄍ ㄍ ㄍ ㄍcos ㄍ ㄍ ㄍ ㄍcos ​ 从以上公式中解出 cos ， cos ， cos ，则可以得到余弦定理的另一 种形式： ​ cos ㄍ ㄍ ㄍ ㄍ cos ㄍ ㄍ ㄍ ㄍ cos ㄍ ㄍ ㄍ ㄍ 判断三角形形状 利用三角恒等变换、正弦定理和余弦定理进行边角互化，从而找到三角形元素之间的关系，进 而判断三角形形状． 三角形的面积 ​ ㄍ ㄍ ㄍ （ 、 、 分别表示 、 、 上的高） ​ ㄍ sin ㄍ sin ㄍ sin ，其中 ㄍ （海伦公式） 解三角形的应用 利用正弦定理、余弦定理解决实际测量中的一些问题． 精选例题 解三角形 1. 若锐角三角形 的面积为 ㄍ ， ㄍ ， ，则 cos ． 【答案】 ㄍ 2. 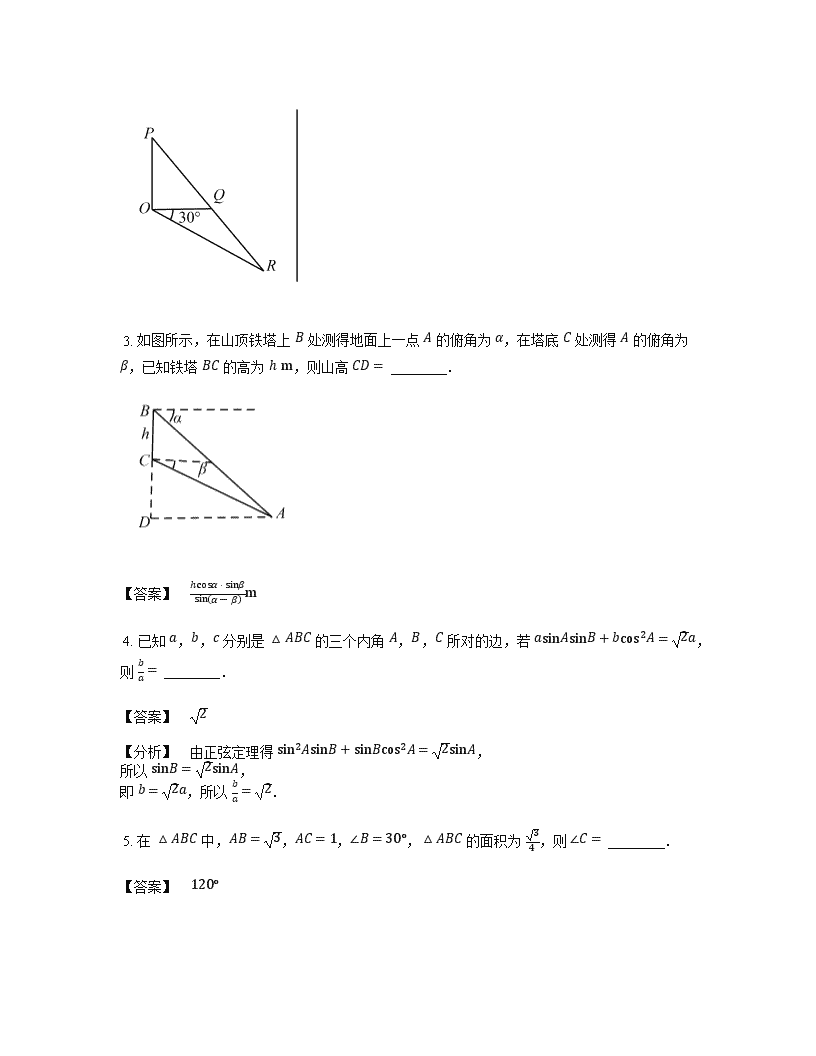在 点测量到远处有一物体在做匀速直线运动，开始时刻物体于 点，一分钟后，其位置 在 点，且 ，再过一分钟，该物体位于 ㌰ 点，且 ㌰ ，则 tan ． 【答案】 ㄍ【分析】 根据题意， ㌰ ，不妨设其长度为 ，在 Rt 中， sin ， cos ，在 ㌰ 中，由正弦定理得 ㄍ sin sin㌰ cos sin㌰ ，同理在 ㌰ 中， 由正弦定理得 sin sin㌰ sin sin㌰ ，两式两边同时相除得 sin sinㄍ ㄍ sin sin sin㌰ cos tan tan sinㄍ ㄍsin ㄍ ． 3. 如图所示，在山顶铁塔上 处测得地面上一点 的俯角为 ，在塔底 处测得 的俯角为 ，已知铁塔 的高为 m ，则山高 㤵 ． 【答案】 cossin sin m 4. 已知 ， ， 分别是 的三个内角 ， ， 所对的边，若 sinsin cos ㄍ ㄍ ， 则 ． 【答案】 ㄍ【分析】 由正弦定理得 sin ㄍ sin sincos ㄍ ㄍsin ， 所以 sin ㄍsin ， 即 ㄍ ，所以 ㄍ ． 5. 在 中， ， ， ， 的面积为 ，则 ． 【答案】 ㄍ 6. 如图，在海岸 处发现北偏东 方向上，距 处（ ）海里的 处有一艘走私 船．在 处北偏西 方向上，距 处 ㄍ 海里的 处的我方缉私船奉命以 海里 小时 的速度追截走私船，此时走私船正以 海里 小时的速度，从 处向北偏东 方向逃 窜．问：缉私船沿什么方向行驶才能最快截获走私船？并求出所需时间． 【解】 如图，设缉私船应沿 㤵 方向行驶 小时，才能最快截获（在 㤵 点）走私船， 则 㤵 海里， 㤵 海里， 在 中，由余弦定理，有 ㄍ ㄍ ㄍ ㄍ cos ㄍ ㄍ ㄍ ㄍ ㄍ cosㄍ 晦䁑 解得 晦 （海里）． 又因为 sin sin ， 所以 sin sin ㄍsinㄍ 晦 ㄍ ㄍ ， 可知 ， 所以 点在 点的正东方向上， 所以 㤵 ㄍ ， 在 㤵 中，由正弦定理，得 㤵 sin㤵 㤵 sin㤵 ， 所以 sin㤵 㤵sin㤵 㤵 sinㄍ ㄍ ． 可知 㤵 ． 因为在 㤵 中， 㤵 ㄍ ， 㤵 ， 所以 㤵 ， 所以 㤵 ， 即 晦 ． 所以 晦 ， 易知 晦 小时 分钟． 所以缉私船应沿北偏东 晦 的方向行驶，才能最快截获走私船，大约需要 分钟． 7. 已知 的角 ， ， 所对的边分别是 ， ， ，设向量 䁑 ， sin䁑cos ， 䁑 ． (1)若 ，求角 的大小； 【解】 因为 ，所以 cos sin ， 在 中，由正弦定理得： sin sin ， 所以 cos sin ，即 tan ， 所以 π ． (2)若 ，边长 ㄍ ，角 π ，求 的面积． 【解】 因为 ，所以 ， 又因为 ㄍ ， π ， 由余弦定理 ㄍ ㄍ ㄍ ㄍcos 得： ㄍ ， 解得： ， 所以 ㄍ sin ㄍ ㄍ ． 8. 已知 ， ， 为 的三内角，且其对应边分别为 ， ， ，若 coscos sinsin ㄍ ． (1)求 ； 【解】 因为 coscos sinsin ㄍ ， 所以 cos ㄍ ， 又因为 a a π ， 所以 π ， 因为 π ， 所以 ㄍπ ． (2)若 ㄍ ， ㄍ ，求 的面积． 【解】 因为 ㄍπ ， 所以 sin ㄍ ， 所以 ㄍ sin ㄍ ㄍ ． 9. 在锐角 中， ， ，且 ， 是方程 ㄍ ㄍ ㄍ 的两根， ㄍsin ．求角 的度数及 的长． 【解】 由 ㄍsin ，得 sin ㄍ ， 因为 为锐角三角形，所以 ㄍ ，所以 晦 ， 因为 ， 是方程 ㄍ ㄍ ㄍ 的两根， 所以 ㄍ ， ㄍ ， 所以 ㄍ ㄍ ㄍ ㄍcos ㄍ 晦 ， 所以 晦 ，即 的长为 晦 ． 10. 三角形 中，已知 sin ㄍ sin ㄍ sinsin sin ㄍ ，其中，角 ， ， 所对的边分别 为 ， ， ． (1)求角 的大小 【解】 由 sin ㄍ sin ㄍ sinsin sin ㄍ ，利用正弦定理化简得： ㄍ ㄍ ㄍ ， 所以 cos ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ ， 即 ㄍπ ． (2)求 的取值范围 【解】 因为由（1）可得： π ，所以由正弦定理可得： sin sin sin sin sin π ㄍ ㄍ cos ㄍ sin ㄍ sin π ㄍ 因为 a a π ， π a π a ㄍπ ， ㄍ a sin π a ， 所以 ㄍ ㄍ a sin π ㄍ a ㄍ ，从而解得： 䁑 ㄍ ． 正弦定理 1. 在 中，内角 ， ， 所对的边分别为 ， ， ，若 ， π ， sin ，则 ． 【答案】 ㄍ 【分析】 由 sin sin ，得 sin π ， 所以 ㄍ ． 2. 在 中， 晦 ， ㄍ 晦 ， ，则 ． 【答案】 【分析】 由正弦定理得 sin ㄍ ㄍ ，所以 或 ． 又因为 晦 ，所以 ，则 ． 3. 在 中， 晦 ， ， ㄍ ，则此三角形的最小边长为 ． 【答案】 ㄍ ㄍ【分析】 由题意知 t 晦 ， 由大角对大边，可知 边最小． 由正弦定理得 sin sin ㄍsin sin ㄍsin sin ㄍ ㄍ ． 4. 在 中， ， ㄍ ， ，若这个三角形只有一解，则 的取值范围 是 【答案】 ㄍ ㄍ 或 a ㄍ【分析】 如图，本题是研究解三角形中两边一对角的情况，应分不同情况讨论，结论如图， 应用数形结合思想可得． 5. 在锐角 中， ㄍ ， ㄍ ，则 的取值范围是 ． 【答案】 ㄍ ㄍ 䁑 ㄍ 【分析】 由正弦定理得 sin sin ，所以 sinㄍ ㄍ sin ，所以 cos ， 又 是锐角三角形，所以 a a t ，且 a ， 又 ㄍ ，所以 a a ， 所以 ㄍ ㄍ a cos a ㄍ ，即 的取值范围是 ㄍ ㄍ 䁑 ㄍ ． 6. 在 中， ， ㄍ ， ，则 sin 的值为 ． 【答案】 ㄍ 7. 的内角 ， ， 的对边分别为 ， ， ，已知 cos cos ， ㄍ ，求 ． 【解】 由 π ，得 cos cos 于是 cos cos cos cos ㄍsinsin䁑 由已知得 sinsin ㄍ 䁑쳌쳌ㄳ由 ㄍ 及正弦定理得 sin ㄍsin䁑쳌쳌 由①②得 sin ㄍ ，于是 sin ㄍ 舍去 或 sin ㄍ 又 ㄍ ，所以 π 晦 8. 在 中， cos cos ． (1)证明： ； 【解】 在 中，由正弦定理及已知得 sin sin cos cos 于是 sincos cossin 䁑 即 sin 因为 π a a π䁑 从而 ．所以 ． (2)若 cos ，求 sin π 的值． 【解】 由 π 和（1）得 π ㄍ䁑 故 cosㄍ cos π ㄍ cos 又 a ㄍ a π ，于是 sinㄍ cos ㄍ ㄍ ㄍ ㄍ 从而 sin ㄍsinㄍcosㄍ ㄍ 䁑cos cos ㄍ ㄍ sin ㄍ ㄍ 所以 sin π sincos π cossin π ㄍ t 9. 在 中，角 ， ， 的对边分别是 ， ， ，且 ， t ， 晦 ． (1)求 sin 的值； 【解】 由正弦定理得， sin sin ， 因为 ， t ， 晦 ， 所以 sin sin ㄍ ． (2)求 cos 的值． 【解】 由（1）得， sin ㄍ ，且 ᦙ ， 所以 cos sin ㄍ ， 又因为 晦 ， 所以 sin ㄍ ， cos ㄍ ， 所以 cos cos sinsin coscos ㄍ ㄍ ㄍ 晦 10. 如图所示，在四边形 㤵 中， 平分 㤵 ， 晦 ， ， 㤵 晦 ， 㤵 ㄍ ，求 的长． 【解】 在 㤵 中， 㤵 ㄍ 㤵sin ， 所以 sin ㄍ㤵 㤵 ㄍ ㄍ 晦 ， 所以 sinㄍ ， 在 中， sinㄍ sin晦 ， 且 cosㄍ sin ㄍ ㄍ ， 所以 ㄍ ㄍ ㄍ ㄍ cosㄍ ， 即 ㄍ ㄍ ， t ， 所以 t 或 ． 11. 在一个直角边长为 m 的等腰直角三角形 的草地上，铺设一个也是等腰直角三角形 ㌰ 的花地，要求 ， ， ㌰ 三点分别在 的三条边上，且要使 ㌰ 的面积最小．现 有两种设计方案： 方案一：直角顶点 在斜边 上， ㌰ ， 分别在直角边 ， 上； 方案二：直角顶点 在直角边 上， ㌰ ， 分别在直角边 ，斜边 上．请问应选用哪一 种方案？并说明理由． 【解】 方案一：过 做 于 ，作 于 ， 因为 ㌰ 为等腰直角三角形，且 ㌰ ， 所以 ㌰ ， 所以 ， 从而 为 的中点， 则 m ， 设 ㌰ ，则 ㌰ cos ， 䁑 所以 ㌰ ㄍ ㌰ ㄍ ㄍ ㄍcos ㄍ ， 所以 ㌰ 的最小值为 ㄍ ㄍ m ㄍ ； 方案二： 设 ， ㌰ ， 䁑 ， 在 ㌰ 中， ㌰ cos ， 在 中， ， 所以 sin sin ，即 ㄍ ㄍ cos sin ， 化简为： cos sinㄍcos ， 所以 ㌰ ㄍ ㌰ ㄍ sinㄍcos ㄍ ， 因为 sin ㄍcos ㄍ ， 所以 ㌰ 的最小值为 m ㄍ ． 综上，应选用方案二． 12. 中，其内角 ， ， 所对的边 ， ， 满足 ㄍ ㄍ ，且 晦 ，求 ． 【解】 因为 晦 ， 所以 ㄍ ， 由 ㄍ ㄍ 及正弦定理得， ㄍsin ㄍ sinsin ， 所以 sinsin ㄍ ， 又 cos coscos sinsin coscos ㄍ cosㄍ ㄍ ， 所以 coscos ， 所以 cos 或 cos ， 所以 或 ． 余弦定理 1. 在 中， ， π ，则 的面积为 ． 【答案】 【分析】 由余弦定理得 ㄍ ㄍ ㄍ ㄍcos ㄍ ㄍ ，由 得 ㄍ ㄍ ㄍ ㄍ ， 所以 ， 所以 的面积为 ㄍ sin ． 2. 在 中， ㄍ ， ㄍ ，正弦等于 ㄍ ，则三边长为 ． 【答案】 ， ， 【分析】 由题意知 边最大， sin ㄍ ， 所以 ㄍ ， 所以 ㄍ ㄍ ㄍ ㄍcos ． 所以 ㄍ ㄍ ㄍ ㄍ ㄍ ． 所以 ㄍ ， ㄍ （舍去）， ． 所以 ㄍ ， ㄍ ． 3. 在 中，角 、 、 所对的边分别是 、 、 ，若 cos cos ㄍ ，则 ． 【答案】 ㄍ 【分析】 由 cos cos ㄍ 得 ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ ， 所以 ㄍ ． 4. 的内角 ， ， 的对边分别为 ， ， ，若 ㄍ ㄍ ， π 晦 ，则 ． 【答案】 π 【分析】 由余弦定理，得 ㄍ ㄍ ㄍ ，与 ㄍ ㄍ 联立，得 ㄍ ，即 ，代入 ㄍ ㄍ ，得 ㄍ ㄍ ，解得 ， 所以 ㄍ ， 所以 cos ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ ㄍㄍ ㄍ ， 所以 π ． 5. 在 中， ， ， 分别为角 ， ， 的对边， ， ， ，则 ． 【答案】 或 ㄍ 6. 已知三角形的三边为 ， ， 和面积 ㄍ ㄍ ，则 cos ． 【答案】 【分析】 由已知得 ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ ㄍcos ㄍ ． 又 ㄍ sin ， 所以 ㄍ sin ㄍ ㄍcos ． 所以 cos sin ，平方得 cos ㄍ ㄍcos ． 所以 cos cos ． 所以 cos （舍去）或 cos ． 7. 设 的内角 ， ， 的对边分别为 ， ， ，已知 䁑 ， 䁑 ，且 ． (1)求角 的大小； 【解】 由 ， 得 䁑 䁑 䁑 即 ， 即 ㄍ ㄍ ㄍ ． 由余弦定理得 cos ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ 䁑又因为 a a π ， 所以 π 晦 ． (2)计算 ㄍsincos sin 的值． 【解】 ㄍsincos sin ㄍsincos sincos cossin sincos cossin sin sin π sin π 晦 ㄍ 8. 在 中，已知 ， 㤵 是 边上的一点， 㤵 ， ， 㤵 晦 ，求 的长． 【解】 在 㤵 中， 㤵 ， ， 㤵 晦 ， 由余弦定理得 cos㤵 㤵 ㄍ 㤵 ㄍ ㄍ ㄍ㤵㤵 晦晦 ㄍ晦 ㄍ ， 所以 㤵 ㄍ ， 所以 㤵 晦 ． 在 㤵 中， 㤵 ， ， 㤵 晦 ． 由正弦定理得 sin㤵 㤵 sin ， 所以 㤵sin㤵 sin sin晦 sin ㄍ ㄍ ㄍ 晦 ． 9. 设 是锐角三角形， ， ， 分别是内角 、 、 所对边长，并且 sin ㄍ sin π sin π sin ㄍ (1)求角 的值； 【解】 因为 sin ㄍ ㄍ cos ㄍ sin ㄍ cos ㄍ sin sin ㄍ cos ㄍ sin ㄍ sin ㄍ 䁑所以 sin ㄍ 䁑又 为锐角，所以 π (2)若 ㄍ ， ㄍ ，求 䁑 （其中 a ）． 【解】 由 ㄍ ，可得 cos ㄍ쳌쳌ㄳ 由（1）知 π ，所以 ㄍ䁑쳌쳌 由余弦定理知 ㄍ ㄍ ㄍ ㄍcos䁑 将 ㄍ 及 代入，得 ㄍ ㄍ ㄍ䁑쳌쳌得 得 ㄍ ，得 ㄍ 䁑 即 因此， ， 是一元二次方程 ㄍ ㄍ 的两个根． 解此方程并由 ᦙ 知 晦䁑 10. 设 的三内角 ， ， 所对的边分别为 ， ， ，函数 cos ㄍ sin sin ㄍ ㄍ ， 且 ㄍ ． (1)求 的大小； 【解】 cos ㄍ sin cos ㄍ ㄍ sin ㄍ cos ㄍ sin π 晦 ㄍ 因为 sin π 晦 ㄍ ㄍ ， 所以 sin π 晦 ． 由 a a π ，得 π 晦 a π 晦 a π 晦 ， 所以 π 晦 π ㄍ ，即 π ． (2)若 ，求 的最小值． 【解】 因为 ㄍ ㄍ ㄍ ㄍcos ， 所以 ㄍ ㄍ ㄍ ， 即 ． 又因为 ㄍ ㄍ ， 所以当且仅当 时， 的最小值为 ㄍ ． 11. 在 中，内角 ， ， 所对的边长分别是 ， ， ，已知 π ， cos ． (1)求 cos 的值； 【解】 因为 cos ，且 䁑π ， 所以 sin cos ㄍ ． cos cos π cos π cos π cos sin π sin ㄍ ㄍ ㄍ ㄍ ㄍ (2)若 ， 㤵 为 的中点，求 㤵 的长． 【解】 由（ ）可得 sin cos ㄍ ㄍ ㄍ ㄍ ． 由正弦定理得 sin sin ，即 ㄍ ㄍ ㄍ ，解得 ． 在 㤵 中， 㤵 ， 㤵 ㄍ ㄍ ㄍ ㄍ ， 所以 㤵 ． 12. 中，角 ， ， 对边分别是 ， ， ，满足 ㄍ ㄍ ㄍ ． (1)求角 的大小； 【解】 由已知 ㄍcos ㄍ ㄍ ㄍ ㄍ ， 由余弦定理 ㄍ ㄍ ㄍ ㄍcos 得 cos ㄍ ，所以 cos ㄍ ， 因为 a a π ，所以 ㄍπ ． (2)求 ㄍ cos ㄍ ㄍ sin π 的最大值，并求取得最大值时角 ， 的大小． 【解】 因为 ㄍπ ，所以 π ， a a π ． ㄍ cos ㄍ ㄍ sin π ㄍ cos ㄍ sin π ㄍsin π 因为 a a π ，所以 π a π a ㄍπ ， 所以当 π π ㄍ ， ㄍ cos ㄍ ㄍ sin π 取最大值 ㄍ ，解得 π 晦 ． 判断三角形形状 1. 在 中，已知 ㄍcossin sin ，则 的形状是 ． 【答案】 等腰三角形 2. 在 中， cos cos ，则该三角形是 三角形． 【答案】 等腰 【分析】 由条件得 sin ． 3. 已知 sinㄍ sinㄍ ，则 的形状为 ． 【答案】 等腰或直角三角形 【分析】 ㄍ ㄍ 或 ㄍ ㄍ π ，所以 为等腰或直角三角形． 4. 中，若 sinsin a coscos ，则这个三角形是 三角形． 【答案】 钝角 【分析】 因为 coscos ᦙ sinsin ， 所以 coscos sinsin ᦙ ， 即 cos cos ᦙ ，即 cos a ． 又 䁑π ，所以 为钝角． 5. 在 中，三个内角 ， ， 的对边分别是 ， ， ，若 ㄍcoscos cos ，则 是 三角形． 【答案】 等腰 【分析】 π ， cos cos ， ㄍcoscos cos cos ， ㄍcoscos coscos sinsin ， cos ， ，即 ． 6. 在 中，内角 ， ， 所对的边长分别为 ， ， ，若 sin sin sinㄍ 试 判断 的形状． 【解】 由已知得 sin sin sinㄍ ， sinsin cossin sincos cossin sinㄍ ， ㄍcossin ㄍsincos ， cos sin sin ． 所以 cos 或 sin sin ， 所以 或 ． 所以 是直角三角形或等腰三角形． 7. 已知 ， ， 分别是 的三个内角 ， ， 所对的边． (1)若 面积 ㄍ ， ㄍ ， 晦 ，求 ， 的值； 【解】 因为 ㄍ sin ㄍ ， 所以 ㄍ ㄍsin晦 ㄍ ，得 ， 由余弦定理得： ㄍ ㄍ ㄍ ㄍcos ㄍ ㄍ ㄍ ㄍ ㄍ cos晦 ， 所以 ． (2)若 cos 且 sin ，试判断 的形状． 【解】 由余弦定理得： ㄍ ㄍ ㄍ ㄍ ， 所以 ㄍ ㄍ ㄍ所以 ； 在 Rt 中， sin ， 所以 ， 所以 是等腰直角三角形． 8. 根据下列条件，判断三角形的形状． (1)在 中， cos cos ； 【解】 由正弦定理得 ㄍ㌰ sin ， ㄍ㌰ sin （ ㌰ 为 的外接圆的半径）． 代入 cos cos ，整理得 sinㄍ sinㄍ ，化积得 ㄍcos sin ． a a π ， a a π ， π a a π ． 假设 sin ，则 ， ，这与已知 矛盾， sin ． cos ， π ㄍ ，即 π ㄍ ． 是直角三角形． (2)在 中， ㄍ ，且 sinsin ． 【解】 由已知条件，得 ㄍ ， ㄍ ㄍ ㄍ ． ， ㄍ ㄍ ㄍ ， ㄍ ㄍ ㄍ ． 又 ㄍ ㄍ ㄍ ㄍcos ， cos ㄍ ， π ． 由 sin sin ， 得 ㄍ cos cos ， ㄍ cos cos ， cos ． π a a π ， ，即 ． π ， 为等边三角形． 9. 在 中，若 cos cos ，试判断三角形的形状． 【解】 由正弦定理，得 cos cos sin sin ， sincos sincos ， sinㄍ sinㄍ ， ㄍ ㄍ ，或 ㄍ ㄍ π ， ，或 π ㄍ ． 又 ᦙ ，即 ᦙ ， ᦙ ， π ㄍ ，从而 为直角三角形． 10. 在 中，已知 cos cos cos ， ㄍcos ，试判断 的形状． 【解】 ㄍcos ，由正弦定理可得， ㄍsincos sin sin sincos cossin ， sincos cossin ，即 sin ， ， ， ， cos cos ， cos cos cos ， cos ， ， cos ， π ㄍ ， 是等腰直角三角形． 三角形的面积 1. 已知 的三边长分别为 ， ， 晦 ，则 的面积为 ． 【答案】 2. 已知 中， t ， ， t ，则 等于 ． 【答案】 晦 或 ㄍ 3. 已知 ， ， 分别为 三个内角 ， ， 的对边， ㄍ ，且 ㄍ sin sin sin ，则 面积的最大值为 ． 【答案】 【分析】 因为 ㄍ ，所以 ㄍ sin sin sin 即为 sin sin sin ， 由正弦定理可得 ，即 ㄍ ㄍ ㄍ ， 由余弦定理可得 cos ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ ，又 a a π ，故 π ， 所以 cos ㄍ ㄍ ㄍ ㄍ ᦙ ㄍ ㄍ ，所以 ，当且仅当 时取等号，由三角形面积公式知 ㄍ sin ㄍ ㄍ ， 故 面积的最大值为 ． 4. 在 中， sin cos ㄍ ㄍ ， ， ，则 的面积是 ． 【答案】 ㄍ 晦 ㄍ 【分析】 根据题意， sin cos ㄍsin π ㄍ ㄍ a ，所以 sin π ㄍ 且 为锐 角，所以 π π 晦 ，即 π ㄍ ． 的面积为 ㄍ sin π ㄍ ㄍ 晦 ㄍ ． 5. 满足条件 ㄍ ， ㄍ 的三角形 的面积的最大值是 ． 【答案】 ㄍ ㄍ【分析】 设 ，则 ㄍ ，根据面积公式，得 ㄍ sin cos ㄍ ． 根据余弦定理，得 cos ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ ， 于是 ㄍ ㄍ ㄍt ㄍㄍ ㄍ 晦 ． 由三角形三边关系有 ㄍ ᦙ ㄍ䁑 ㄍ ᦙ ㄍ䁑 解得 ㄍ ㄍ ㄍ a a ㄍ ㄍ ㄍ ，故当 ㄍ 时， 取 到最大值 ㄍ ㄍ ． 6. 在 中，角 ， ， 所对的边分别为 ， ， ． (1)若 cos sin ，求角 ； 【解】 因为 cos sin ， 由正弦定理可得 sincos sinsin sin sin ． 即 sincos sinsin sincos cossin ． 即 sinsin cossin ， 所以 sin cos ， 所以 tan ， 所以 晦 ． (2)若 ， ㄍ ，且 的面积为 ，求 的值． 【解】 解法一：因为 ， 的面积为 ， 所以 ㄍ sin ． 所以 ㄍ sin ㄍ ， 所以 sin ㄍ ㄍ 䁑쳌쳌ㄳ由余弦定理 ㄍ ㄍ ㄍ ㄍcos ， 所以 ㄍ ㄍ ㄍ cos ， 所以 cos ㄍ ㄍ ㄍ ㄍ 䁑쳌쳌由 ㄳ ， 得： ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ ， 化简得 t ㄍ 晦 ， 所以 ㄍ ㄍ ， 所以 ㄍ ． 解法二：由 ㄍ sin 得 ㄍ sin ㄍ䁑쳌쳌ㄳ由 ㄍ ㄍ ㄍ cos 得 ㄍ ㄍ cos ㄍ䁑쳌쳌由 ㄳ ， 得： sin ㄍ cos ，即 sin π ， 所以 π 晦 ， ㄍ ㄍ sin ． 所以 ㄍ ． 7. 在 中，若一直三边为连续正整数，最大角为钝角． (1)求最大角的余弦值； 【解】 设这三个数为 ， ， ㄍ 最大角为 ， 则 cos ㄍ ㄍ ㄍ ㄍ ㄍ a 䁑化简得 ㄍ ㄍ a 得 a a ． 又因为 且 ᦙ 䁑 所以 a a ， 所以 ㄍ ． 所以 cos 晦 ㄍㄍ ． (2)求以此最大角为内角，夹此角的两边之和为 的平行四边形的最大面积． 【解】 设此平行四边形的一边长为 䁑 则夹角 角的另一边长长为 ， 平行四边形的面积为 ·sin ㄍ ㄍ ㄍ ≤ 当且仅当 ㄍ 时， max ． 8. 如图， 中， 边上的高为 㤵 ．求证： 的面积 ㄍ sin ． 【解】 由题意知 ㄍ 㤵 ， 在 ㌰ 㤵 中， 㤵 sin ， 所以 ㄍ sin ． 9. 在 中，三个内角 ， ， 满足 sin ㄍ sin ㄍ sin ㄍ sin sin ，若 cm ， cm ，求 的值． 【解】 由条件及正弦定理得 ㄍ ㄍ ㄍ ． ㄍ ㄍ ㄍ ㄍ ㄍ ． 由余弦定理得 cos ㄍ ，则 晦 ． ㄍ sin ㄍ ㄍ （ cm ㄍ ）． 10. 在 中，角 ， ， 所对的边分别为 ， ， ， ㄍ ， sin ． (1)求 cos 及 sin 的值； 【解】 因为 ㄍ ， 所以 cos cosㄍ ㄍsin ㄍ ． 因为 sin ， 所以 cos ㄍ ． 由题意可知， 䁑 π ㄍ ． 所以 cos sin ㄍ 晦 ． 因为 sin sinㄍ ㄍsincos ㄍ ㄍ ． 所以 sin sin π sin sincos cossin ． (2)若 ㄍ ，求 的面积． 【解】 因为 sin sin ， ㄍ ， 所以 ㄍ ㄍ ㄍ ． 所以 晦 ． 所以 ㄍ sin ㄍ ㄍ ． 解三角形的应用 1. 某同学骑电动车以 ㄍkmh 的速度沿正北方向的公路行驶，在点 处测得电视塔 在电动 车的北偏东 方向上， min 后到点 处，测得电视塔 在电动车的北偏东 方向上， 则点 与电视塔的距离是 km ． 【答案】 ㄍ【分析】 如图所示，由题意知 ㄍ 晦 晦 ，在 中， ， 晦 ， t ， 所以 ．由正弦定理知 sin sin ，所以， sin sin ㄍ ． 2. 如图所示，设 ， 两点在河的两岸，一测量者在 的同侧，在 所在的河岸边选定一点 ， 测出 的距离为 m ， ， 后，就可以计算 ， 两点的距离 为 ． 【答案】 ㄍm【分析】 因为 ， ， 所以 ． 由正弦定理得 sin sin ， 即 ㄍ ㄍ ㄍ ， 可得 ㄍm ． 3. 如图，在铁路建设中需要确定隧道长度和隧道的施工方向．已测得隧道两道墙两年端点的 两点 ， 到某一点 的距离分别为 ㄍ 千米、 ㄍ 千米及 ，则 ， 两点间得距 离为 千米． 【答案】 ㄍ 4. 如下图，为了测定河的宽度，在河岸取定基线 ，其长为 ，在河对岸取定点 ，测得 ， ，则河的宽度为 ． 【答案】 sinsin sin 【分析】 由角 ， 可得 ，由正弦定理可求得 或 的长，过 作 㤵 于 㤵 ， 由 Rt 可求得 㤵 即河的宽度． 由题意可知： π ， 在 中， sin sin sin sin ， 所以 㤵 sin sinsin sin ． 5. 如图，为了测量两座山峰上两点 ， 之间的距离，选择山坡上一段长度为 米且和 ， 两点在同一平面内的路段 的两个端点作为观测点，现测得四个角的大小分别是 ， 晦 ，可求得 ， 两点间的距离为 米． 【答案】 【分析】 令 和 相交于点 ，则： 由图象可知 ，又因为 晦 ，所以 ， 所以 为等腰三角形． 所以 ， ，所以 为等腰三角形． 又因为 晦 ，所以 为等腰三角形，所以 ． 在直角三角形 中， ，易求出 ，所以 ． 6. 如图，飞机的航线和山顶在同一个铅直平面内，已知飞机的高度为海拔 ㄍ 米，速度为 米/分钟．飞行员先在点 看到山顶 的俯角为 ，经过 t 分钟后到达点 ，此时看到 山顶 的俯角为 晦 ，求山顶的海拔高度． （参考数据： ㄍ ， ㄍ ， 晦 ㄍ ） 【解】 如图， 过 作 的垂线，垂足为 㤵 ． 依题意， t ㄍ （米）， 又 ， 㤵 晦 ，则 ． 故 ㄍ 米． 在 Rt 㤵 中， 㤵 㤵sin晦 ㄍ t晦晦 ㄍt （米）． 故山顶的海拔高度约为 ㄍ ㄍt ㄍ晦 （米）． 7. 如图，当甲船位于 处时获悉，在其正东方向相距 ㄍ 海里的 处有一艘渔船遇险等待营 救．甲船立即前往救援，同时把消息告知在甲船的南偏西 ，相距 海里 处的乙船，试 问乙船应朝北偏东多少度的方向沿直线前往 处救援（角度精确到 ）？（参考数据： sin ） 【解】 连接 ，在 中由余弦定理得： ㄍ ㄍ ㄍ ㄍ ㄍ ㄍ cosㄍ ， 于是， ， 在 中由正弦定理得： sin sinㄍ ， 故 ㄍ sin sinㄍ ， 所以 sin ， 又因为 sin ，所以 ， ， 所以乙船应朝北偏东 方向沿直线前往 处救援． 8. 如图，为测算河两岸上 ， 两目标的距离，在岸边取 、 㤵 两点，测得 㤵 ㄍm ， 㤵 ， 㤵 ， 㤵 ㄍ ， 㤵 ，求 ， 间距离． 【解】 如图， 在 㤵 中，由于 㤵 ， 㤵 ㄍ ． 㤵 ， 又 㤵 ㄍ ，根据正弦定理， 㤵 ㄍsinㄍ sin 晦 ． 在 㤵 中， 㤵 ， 㤵 ， 㤵 ． 根据正弦定理， 㤵 ㄍsin sin ㄍ ． 连 ，易求得 㤵 ． 所以 㤵 为直角三角形． 㤵 ㄍ 㤵 ㄍ ㄍ ㄍ m ． 9. 在某次军事演习中红方为了准确分析战场形势，在两个相距为 ㄍ 的军事基地 和 㤵 测得 蓝方两支精锐部队分别在 处和 处，且 㤵 ， 㤵 ， 㤵 晦 ， ，如图所示，求蓝方这两支精锐部队的距离． 【解】 解法一： 㤵 㤵 㤵 晦 ， 㤵 晦 ， 㤵 晦 ， 㤵 㤵 ㄍ ， 在 㤵 中， 㤵 t ， 由正弦定理，得 㤵 sin㤵 㤵 sin㤵 ， 㤵 㤵 sin㤵 sin㤵 ㄍ 晦 ㄍ ㄍ ㄍ ． 在 㤵 中，由余弦定理，得 ㄍ 㤵 ㄍ 㤵 ㄍ ㄍ 㤵 㤵 cos㤵 ㄍ ㄍ ㄍ ㄍ ㄍ t ㄍ 䁑 晦 ， 蓝方这两支精锐部队的距离为 晦 ． 解法二： （同解法一） 㤵 㤵 ㄍ ，在 㤵 中， 㤵 ， sin 㤵 sin ， 晦 ， 在 中，由余弦定理得： ㄍ ㄍ ㄍ ㄍ cos ㄍ t ㄍ ㄍ ㄍ 晦 ㄍ ㄍ t ㄍ 䁑 晦 ， 蓝方这两支精锐部队的距离为 晦 ． 10. 某轮船在海上遇险，一架救援直升机从 地沿北偏东 晦 方向飞行了 km 到 地，再由 地沿正北方向飞行了 km 到达 地，求此时直升机与 地的相对位置． 【解】 由已知可得 ， ㄍ ， ， 由余弦定理可得 ㄍ ㄍ ㄍ ㄍ cos 晦 ，故 ， 所以此时直升机位于 地北偏东 方向，且距离 地 km 处． 课后练习 1. 在不等边三角形 中， 是最大的边，若 ㄍ a ㄍ ㄍ ，则角 的取值范围是 A. π ㄍ 䁑π B. π 䁑 π ㄍ C. π 䁑 π ㄍ D. 䁑 π ㄍ2. 在 中， 、 、 分别为 、 、 的对边，如果 ， π 晦 ，那么 等于 A. ㄍπ B. π C. π 晦 D. π ㄍ 3. 如图，测量河对岸的塔高 时，可以选与塔底 在同一水平面内的两个观测点 与 㤵 ， 测得 㤵 ， 㤵 ， 㤵 米，并在 处测得塔顶 的仰角为 晦 ，则塔的高 度 为 A. ㄍ 米 B. 米 C. 米 D. 晦 米 4. 已知 的三边 ， ， 所对角分别为 ， ， ，且 sin sin ㄍ ，则 cos 的值为 A. ㄍ B. ㄍ C. ㄍ D. ㄍ5. 满足条件 ， ㄍ ， 的 的个数是 A. 一个 B. 两个 C. 无数个 D. 不存在 6. 在 中，若 t ， ㄍ ， ，则此三角形解的情况为 A. 无解 B. 两解 C. 一解 D. 解的个数不确定 7. 在 中，已知三边 ， ， 满足 ㄍ ㄍ ㄍ ，则角 ． 8. 已知三条线段的大小关系为： ㄍ a a ，若这三条线段能构成钝角三角形，则 的取值范 围为 ． 9. 在 中，若 ， ㄍ ，则 的值为 ． 10. 如果等腰三角形的周长是底边长的 倍，那么它的顶角的余弦值为 ． 11. 在钝角 中， ， ㄍ ，则最大边 的取值范围是 ． 12. 在 中，若 ǣǣ ǣㄍǣ ，则 ǣǣ ． 13. 若 ㄍ ， ㄍ ，则有 sinǣsinǣsin ． 14. 在 中，已知 晦 ， ，则 sinsinsin ． 15. 如图， ， ， 是直线上三点， 是直线外一点， ， ， ，则 ． 16. 在 中，角 ， ， 所对的边分别为 ， ， ，已知 ， ㄍ ， sin ，则 sin 的值为 ． 17. 在 中，已知 ǣǣ ǣǣ ，则 ㄍsinsin sin ． 18. 在锐角三角形 中， 晦 ， ㄍ ，则边 的取值范围是 ． 19. 已知 的三个内角为 ， ， ， ㄍsin sin sin ，则 cos 的值是 ． 20. 设函数 sin ㄍ sincos ㄍ ，若 ， ， 分别是 的内角 ， ， 所对的 边， ㄍ ， ， 为锐角，且 是函数 在 䁑 π ㄍ 上的最大值，则 的值 为 ． 21. 已知三角形的两边分别为 和 ，它们的夹角的余弦值是方程 ㄍ 晦 的根，则 三角形的另一边边长为 ． 22. 在 中， ㄍ ， 晦 ， ， 㤵 为边 上的高，则 㤵 的长 是 ． 23. 在 中，内角 ， ， 所对的边分别为 ， ， ．已知 的面积为 ， ㄍ ， cos ，则 的值为 ． 24. 在 中， ㄍcos ，则该三角形的形状为 ． 25. 若 cos π sin π ㄍ ，内角 ， 的对边分别为 ， ，则三角形 的形状 为 ． 26. 在 中，若 ，且 sin ㄍsincos ，则 是 三角形． 27. 已知 ， ， 为 的内角，且 sincos sincos ，则 是 三角形． 28. 在 中， ㄍ ，且 ㄍ ，则 的形状为 29. 已知 的面积为 晦 ， ， ，则 ． 30. 如图，如果 与 㤵䳌䁨 都是正方形网格中的格点三角形（顶点在格点上），那么 㤵䳌䁨ǣ 的值为 ． 31. 已知 的三个内角 、 、 成等差数列，且 ， ，则 的面积 为 ． 32. 已知在 中， ㄍ ， 晦 ， ， 的面积 ． 33. 在 中，已知 晦 ， sin cos ， 的面积 ，则 ， ， ． 34. 如图，当太阳光线与水平面的倾角为 晦 时，一根长为 ㄍm 的竹竿，要使它的影子最长， 则竹竿与地面所成的角为 ． 35. 如图所示，从气球 上测得正前方的河流的两岸 ， 的俯角分别为 ， ，此时气球 的高是 晦m ，则河流的宽度 等于 m ． 36. 如图，某城市的电视台发射塔 㤵 建在市郊的小山上，小山的高 为 米，在地面上有 一点 ，测得 ， 间的距离为 米，从 观测电视发射塔 㤵 的视角 㤵 为 ，则这 座电视台发射塔的高度 㤵 为 ． 37. 如图所示，航空测量组的飞机航线和山顶在同一铅直平面内，已知飞机的飞行高度为 m ，速度为 ms ．某一时刻飞行员看山顶的俯角为 ，经过 ㄍs 后看山顶的俯角 为 ，则山顶的海拔高度为 m ．（参考数据： ㄍ ， ） 38. 如图，测量河对岸的塔高 时，可以选与塔底 在同一水平面内的两个观测点 与 㤵 ， 测得 㤵 ， 㤵 ，并在点 测得塔顶 的仰角为 晦 ，则塔高 ． 39. 如图，在 中， ， 㤵 为 中点， ㄍ ．记锐角 㤵 ．且满足 cosㄍ ㄍ ． (1)求 cos ； (2)求 边上高的值． 40. 一艘船在海上由西向东航行，在 处望见灯塔 在船的东北方向，半小时后在 处望见灯 塔 在船的北偏东 方向，航速为每小时 海里，当船到达 㤵 处时望见灯塔 在船的西北 方向，求 ， 㤵 两点间的距离． 41. 如图所示，一山顶有一信号塔 㤵 （ 㤵 所在的直线与地平面垂直），在山脚 处测得塔尖 的仰角为 ，沿倾斜角为 的山坡向上前进 m 后到达 处，测得 的仰角为 ． (1)求 的长； (2)若 ㄍ ， ， ， ，求信号塔 㤵 的高度． 42. 在 中，内角 ， ， 的对边分别为 ， ， ，且 ， ㄍ 晦 ， ㄍ ． (1)求 cos 的值； (2)求 的值． 43. 在 中，角 ， ， 的对边分别为 ， ， ，已知 cos sin ． (1)求 ； (2)若 ，求 ㄍ 的取值范围． 44. 为扑灭某着火点，现场安排了两支水枪，如图， 㤵 是着火点， ， 分别是水枪位置，已知 ㄍm ，在 处看到着火点的仰角为 晦 ， ， （其中 为 㤵在地面上的射影），求两支水枪的喷射距离至少是多少． 45. 在 中， ， ， 所对的边分别是 ， ， ． (1)用余弦定理证明：当 为钝角时， ㄍ ㄍ a ㄍ ； (2)当钝角 的三边 ， ， 是三个连续整数时，求 外接圆的半径． 46. 在 中， ， ， 所对的边分别为 ， ， ， π 晦 ， ㄍ ． (1)求 ； (2)若 ，求 ， ， ． 47. 已知向量 sin cos䁑 ， cos䁑 ㄍ ，若 ． (1)求函数 的单调递增区间； (2)已知 的三个内角 ， ， 的对边分别为 ， ， ，且 ， ㄍ π ㄍ ㄍ （ 为锐角）， ㄍsin sin ，求 ， ， 的值． 48. 在 中，点 是 上的一点， ， ㄍ ， ， cos ． (1)求线段 的长度； (2)求线段 的长度． 49. 设 的内角 ， ， 的对边分别为 ， ， ，且 cos ㄍ cos ． (1)求 的大小； (2)若 ，则 的最大值． 50. 如图所示，在海岛 上有一座海拔 km 的山，山顶设有一个观察站 ，上午 时，测得 一轮船在岛北偏东 ，俯角为 的 处，到 时 分又测得该船在岛北偏西 晦 ，俯角 为 晦 的 处． (1)求船的航行速度． (2)又经过一段时间后，船到达海岛的正西方向的 㤵 处，问此时船距岛 有多远？ 51. 已知在 中， ， ㄍ ， 晦 ，解此三角形． 52. 在 中，角 䁑䁑 的对边分别为 䁑䁑 ， tan ． (1)求 cos ； (2)若 ㄍ ，且 ，求 ． 53. 同学们对正弦定理的探索与研究中，得到 sin sin sin ㄍ㌰ （ ㌰ 为外接圆的半径）．请 利用该结论，解决下列问题： (1)现有一个破损的圆块如图（1），只给出一把带有刻度的直尺和一个量角器，请你设计一 种方案，求出这个圆块的直径的长度． (2)如图（2），已知三个角满足 sin ㄍ sin ㄍ sin ㄍ sin sin ， 㤵 是外接圆直径， 㤵 ㄍ ， 㤵 ，求 和直径的长． 54. 如图， ， 是单位圆 上的点， 是圆 与 轴正半轴的交点，点 的坐标为 䁑 ，三 角形 为直角三角形． (1)求 sin ， cos ； (2)求线段 的长． 55. 钝角三角形的三边为 ， ， ㄍ ，其中最大的角不超过 ㄍ ，则 的取值范围是什 么？ 56. 在 中，三个内角 ， ， 所对的边分别为 ， ， ， lg lg lgsin lg ㄍ ，且 为锐角，试判断 的形状． 57. 关于 的方程 ㄍ coscos cos ㄍ ㄍ 有一根为 ，判断 的形状． 58. 在 中，已知角 ， ， 的对边分别为 ， ， ，且 cos cos cos ，试判 断 的形状． 59. 在 中，三内角 ， ， 的对边分别是 ， ， ． (1)若 晦 ， ， ㄍ ，求 ； (2)若 ㄍ ㄍ ㄍ ㄍ ， sin ㄍ sinsin ，试判断 的形状． 60. 中， ， ， 所对的边分别为 ， ， ， 䁑ㄍ ， cosㄍ䁑cos ㄍ ㄍ ，且 ． (1)求 的大小； (2)若 ㄍ ㄍ ，求 的面积并判断 的形状． 61. ， ， 㤵 是首尾相接且不在同一个平面内的三条线段，且 ， ， 㤵 的三等分点分 别是 ， ； ㄍ ， ㄍ ； ， ．求证： (1)平面 ㄍ 平面 ㄍ ； (2) ㄍ 与 ㄍ 面积相等． 62. 某城市广场有一块不规则的绿地如图所示，城建部门欲在该地上建造一个底座为三角形的 环境标志，小李、小王设计的底座形状分别为 ， 㤵 ，经测量 㤵 㤵 m ， m ， tm ， 㤵 ． (1)求 的长度； (2)若不考虑其他因素，小李、小王谁的设计使建造费用较低（请说明理由）． 63. 在 中，角 ， ， 所对的边分别为 ， ， ．已知 ㄍsinsin ㄍsin ㄍ ㄍsin ㄍ cosㄍ ． (1)求角 的大小； (2)若 ㄍ ，且 的面积为 ㄍ ，求边 的长． 64. 在 中，内角 ， ， 所对的边分别为 ， ， ，已知 sin tan tan tantan ． (1)求证： ， ， 成等比数列； (2)若 ， ㄍ ，求 的面积 ． 65. 在 中，内角 䁑䁑 所对的边分别是 䁑䁑 ．已知 cos cos ，边 上的中线长 为 ． (1)若 π 晦 ，求 ； (2)求 面积的最大值． 66. 如图所示， 是海面上一条南北方向的海防警戒线，在 上点 处有一个水声监测点，另 两个监测点 䁑 分别在 的正东方向 ㄍkm 处和 km 处．某时刻，监测点 收到发自目标 的一个声波， ts 后监测点 䁑ㄍs 后监测点 相继收到这一信号，在当时的气象条件下，声 波在水中的传播速度是 km ． (1)设 到 的距离为 km ，用 分别表示 䁑 到 的距离，并求 的值； (2)求目标 的海防警戒线 的距离（精确到 km ）． 67. 隔河看两目标 与 ，但不能到达，在岸边选取相距 km 的 ， 㤵 两点，测得 ， 㤵 ， 㤵 ， 㤵 （ ， ， ， 㤵 在同一平面内），求两目标 ， 之间的距离． 68. 已知飞机从甲地按北偏东 的方向飞行 ㄍkm 到达乙地，再从乙地按南偏东 的方 向飞行 ㄍkm 到达丙地，再从丙地向西南方向飞行 ㄍkm 到达丁地，问：丁地在甲地 的什么方向？丁地距甲地多远？ 69. 某人从点 向正东方向走 千米后到达点 ，接着他向左转 ，然后朝新方向走 千米 到达点 ，结果他离出发点恰好为 千米，那么 的值是多少？ 70. 如图，测量河对岸的塔高 时，可以选与塔底 在同一水平面内的两个测点 与 㤵 ．现 测得 㤵 ， 㤵 ， 㤵 ，并在点 测得塔顶 的仰角为 ，求塔高 ． 解三角形-出门考 姓名 成绩 1. 已知在 中， ， ， 的对边分别为 ， ， ，若 晦 ㄍ 且 ， 则 ． 2. 从某电线杆的正东方向的 处测得电线杆顶端的仰角是 晦 ，从电线杆南偏西 晦 的 处 测得电线杆顶端的仰角是 ， ， 间的距离为 米，则此电线杆的高度是 米． 3. 在 中，若 ㄍ ， ， ㄍ ，则 ． 4. 在 中，若 ， ， ㄍπ ，则 ________． 5. 在锐角三角形 中， ， ㄍ ，则 cos 的值等于 ， 的取值范围 为 ． 6. 已知平面内两个非零向量 ， 满足 ，且 与 的夹角为 ，则 的取值 范围是 ． 7. 已知 ， ， 分别是 的三个内角 ， ， 所对的边，若 ， ， ㄍ ，则 sin ． 8. 在 中．若 ， π ， sin ，则 ． 9. 在 中，角 ， ， 所对的边分别为 ， ， ．若 ᦙ ，给出下列四个结论：① ᦙ ；② sin ᦙ sin ；③ cos a cos ；④ tan ᦙ tan ．其中所有正确结论的序号 是 ． 10. 在 中，若 ㄍ ， ǣ ǣ ，则 ． 11. 如图所示，已知四边形 㤵 各边的长分别为 ， ， 㤵 t ， 㤵 ，且点 ， ， ， 㤵 在同一个圆上，则对角线 的长为 ． 12. 在四边形 㤵 中， 㤵 㤵 ， 㤵 ， ， 㤵 晦 ， 㤵 ，则 ． 13. 已知 的三边长成公比为 ㄍ 的等比数列，则其最大角的余弦值为 ． 14. 在 中，若 ㄍ ㄍ ㄍ ，则 cos ． 15. 在 中，内角 、 、 的对边长分别为 、 、 ，已知 ㄍ ㄍ ㄍ ，且 sincos cossin ，则 ． 16. 给出下列三个命题： ①若 tantan ᦙ ，则 一定是钝角三角形； ②若 sin ㄍ sin ㄍ sin ㄍ ，则 一定是直角三角形； ③若 cos cos cos ，则 一定是等边三角形． 以上正确命题的代号为 ． 17. 在 中，若 sin sin sin cos cos ，此三角形的形状是 三角形． 18. 直角三角形 的斜边 在平面 内，直角顶点 在 内的射影是 ，则 的形 状为 ． 19. 已知 中， sin sin ，且 sin ㄍ sin ㄍ sin ㄍ ，则 的形状为 ． 20. 若一个钝角三角形的三条边长分别是 ， ㄍ ， ，则 的取值范围是 ． 21. 在 中，若 sin ， sin ㄍsinsin ，则 的形状为 ． 22. 在 中， ㄍcm ， ㄍcm ， 满足 sin cos ，则 的面积 是 ． 23. 在 中，已知 π ， ， 的面积为 ㄍ ，则 ． 24. 如图，点 为半圆的直径 延长线上一点， ㄍ ，过动点 作半圆的切线 ， 若 ，则 的面积的最大值为 ． 25. 在 中， ㄍ ， ，且 的面积为 ，则 ． 26. 三角形的两边分别为 cm ， cm ，它们所夹角 的余弦为方程 ㄍ 晦 的根，则 这个三角形的面积为 ． 27. 在 中，已知 t ， ，三角形面积为 ㄍ ，则 cosㄍ ． 28. 在湖面上高 米处，测得天空中一朵云的仰角为 ，测得云在湖中影子的俯角为 ，则云 距湖面的高度为 米． 29. 如图，一艘船上午 ǣ 在 处测得灯塔 在它的北偏东 处，之后它继续沿正北方向匀 速航行，上午 ǣ 到达 处，此时又测得灯塔 在它的北偏东 处，且与它相距 t ㄍ 海 里．此船的航速是 海里/小时． 30. 如图，一艘船以 ㄍ 千米/小时的速度向正北航行，船在 处看见灯塔 在船的东北方向， 小时后船在 处看见灯塔 在船的北偏东 的方向上，这时船与灯塔的距离 等 于 千米． 31. 如图，从高为 ㄍ 米的气球 上测量铁桥 的长，如果测得桥头 的俯角 晦 是， 桥头 的俯角是 ，则桥 长为 米． 32. 用同样的两根绳子挂一个物体，如果物体受到重力为 ，且 ttㄍN ，两根绳子的夹角 为 a a π ，绳子受到的拉力为 䁨 、 䁨ㄍ ，则 䁨 与 的关系是 （填写正确序 号）． ① 䁨 随 的增大而增大 ② 䁨 随 的增大而减小 ③不论 如何变化， 䁨 的大小不变 ④ 时， 䁨 最大 33. 在 中，角 ， ， 所对的边分别为 ， ， ，已知 ㄍ cos cos ． (1)求角 的大小； (2)若 ㄍ ，求使 面积最大时 ， 的值． 34. 设 的内角 䁑䁑 所对的边为 䁑䁑 ，且有 ㄍsincos sincos cossin ． (1)求角 的大小； (2)若 ㄍ ， ， 㤵 为 的中点，求 㤵 的长． 35. 在 中， ， ， ，求 ， 和 ． (1)答案： 36. 在 中，角 ， ， 所对边分别为 ， ， ，且 tan tan ㄍ ． (1)求角 ； (2)若 ，试判断 取得最大值时 的形状． 37. 在 中，已知 sin ㄍ sin ㄍ sin ㄍ ，且 sin ㄍsincos ，试判断 的形状． 38. 在 中，角 ， ， 的对边分别为 ， ， ．角 ， ， 成等差数列． (1)求 cos 的值； (2)若边 ， ， 成等比数列，求 sinsin 的值． 39. 中，内角 ， ， 成等差数列，其对边 ， ， 满足 ㄍ ㄍ ，求 ． 40. 中， 㤵 为边 上的一点， 㤵 ， sin ， cos㤵 ，求 㤵 ． 41. 已知 中， ， ㄍ ，则求角 的取值范围． 42. 在 中， ， ㄍ 晦 ， ㄍ ．求 cos 的值． 43. 设 的内角 䁑䁑 的对边长分别为 䁑䁑 ，且 ㄍ ㄍ ㄍ ㄍ ． (1)求 sin 的值； (2)求 ㄍsin π sin π cosㄍ 的值． 44. 在 中，角 、 、 的对边分别为 、 、 ．已知向量 ㄍcos ㄍ 䁑sin ㄍ ， cos ㄍ 䁑 ㄍsin ㄍ ， (1)求 cos 的值； (2)若 ㄍ ， ㄍ ，求 的值． 45. 在 中， ， ， ， 是方程 ㄍ ㄍ ㄍ 的两个根，且 ㄍcos ．求： （1）角 的度数； （2） 的长度． 46. 在 中， ， ， ， 是方程 ㄍ ㄍ 的两个根，且 ㄍcos ，求： (1)角 的度数； (2) 的长度； (3) 的面积． 47. 已知函数 cos sin ㄍ ㄍ ㄍ sin （ ）． (1)求 在 䁑π 上的最大值和最小值． (2)记 的内角 ， ， 所对的边分别为 ， ， ，若 ， ， ，求 的值． 48. 在 中，如果 lg lg lgsin lg ㄍ ，且 为锐角．试判断 的形状． 49. 中， ，且 sin ㄍsincos ，试判断 的形状． 50. 在 中，若 sin sin a coscos ，试判断 的形状． 51. 若三角形的两个内角 ， 满足 cos cos ᦙ sin sin ，试判断此三角形的形状． 52. 在 中， tan tan tantan ，且 tan tan tantan ，试 判断 的形状． 53. 在 中，三个内角 ， ， 所对的边分别为 ， ， ． (1)求证： ㄍ ㄍ ㄍ sin sin ； (2)若 cos ，判断 的形状． 54. 在 中，内角 ， ， 的对边分别为 ， ， ，且 cosㄍ cos ． (1)求角 的大小； (2)若 coscos t ，且 的面积为 ㄍ ，求 ． 55. 在 中，已知 sinㄍ cosㄍ ． (1)求角 的值； (2)若 ㄍ ， π ，求 的面积． 56. 在 中， sin cos ㄍ ㄍ ， ㄍ ， ，求 tan 的值和 的面积． 57. 在 中，内角 ， ， 的对边分别为 ， ， ，已知 cosㄍcos cos ㄍ ． (1)求 sin sin 的值； (2)若 cos ， ㄍ ，求 的面积 ． 58. 在 中， sin cos ㄍ ． (1)求 的大小； (2)现给出三个条件：① ㄍ ；② ；③ ．试从中选出两个可以确定 的条件，写出你的选择并以此为依据求 的面积（只需写出一个选定方案即可，选多种 方案以第一种方案记分）． 59. 如图，在 中，点 㤵 在 边上， 㤵 ， cos 晦 ， ㄍ ， 㤵 ． (1)求 㤵 的面积； (2)求线段 㤵 的长． 60. 如图，海中小岛 周围 t 海里内由暗礁，一艘船正在向南航行，在 处测得小岛 在船 的南偏东 方向，航行 海里后，在 处测得小岛 在船的南偏东 方向，如果此船不 改变航向，继续向南航向，有无触礁的危险？ 61. 如图， 䁑䁑䁑㤵 都在同一个与水平面垂直的平面内， 䁑㤵 为两岛上的两座灯塔的塔顶．测 量船于水面 处测得 点和 㤵 点的仰角分别为 ， ，于水面 处测得 点和 㤵 点的仰 角均为 晦 ， km ．试探究图中 ， 㤵 间距离与另外哪两点间距离相等，然后求 ， 㤵 的距离（计算结果精确到 km ， ㄍ ， 晦 ㄍ ）． 62. 某观测站 在目标 的南偏西 ㄍ 方向，从 出发有一条南偏东 走向的公路，在 处 测得与 相距 km 的公路上的 处，有一人正沿此公路向 走去，走 ㄍkm 到达 㤵 ，此时 测得 㤵 为 ㄍkm ，求此人在 㤵 处距离 还有多少？ 63. 郑州市某广场有一块不规则的绿地如图所示，城建部门欲在该地上建造一个底座为三角形 的环境标志，小李、小王设计的底座形状分别为 、 㤵 ，经测量 㤵 㤵 米， 米， t 米， 㤵 ． (1)求 的长度； (2)若建造环境标志的费用与用地面积成正比．不考虑其他因素，小李、小王谁的设计使建 造费用较低（请说明理由）． 64. 如图，一艘货轮位于海上 处，测得灯塔 位于货轮北偏东 的方向上，随后货轮沿北 偏西 的方向航行．已知货轮的速度为 ㄍnmileh ，半小时后在 处测得灯塔在货轮北偏 东 的方向上，求此时货轮与灯塔的距离．