- 88.99 KB
- 2021-04-17 发布
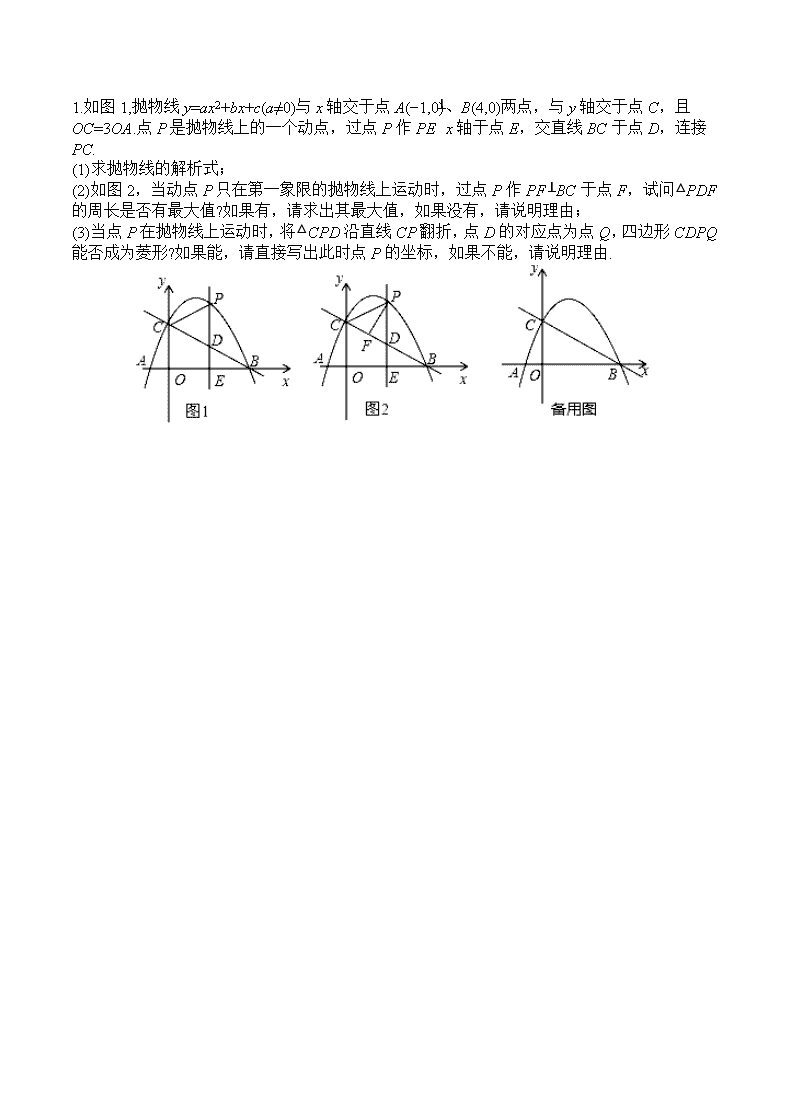
1.如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(−1,0)、B(4,0)两点,与y轴交于点C,且OC=3OA.点P是抛物线上的一个动点,过点P作PE⊥x轴于点E,交直线BC于点D,连接PC.
(1)求抛物线的解析式;
(2)如图2,当动点P只在第一象限的抛物线上运动时,过点P作PF⊥BC于点F,试问△PDF的周长是否有最大值?如果有,请求出其最大值,如果没有,请说明理由;
(3)当点P在抛物线上运动时,将△CPD沿直线CP翻折,点D的对应点为点Q,四边形CDPQ能否成为菱形?如果能,请直接写出此时点P的坐标,如果不能,请说明理由.
2.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,且OA=2,OB=8,OC=6.
(1)求抛物线的解析式;
(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时,点N从B出发,在线段BC上以每秒1个单位长度的速度向C点运动,当其中一个点到达终点时,另一个点也停止运动,当△MBN存在时,求运动多少秒使△MBN的面积最大,最大面积是多少?
(3)在(2)的条件下,△MBN面积最大时,在BC上方的抛物线上是否存在点P,使△BPC的面积是△MBN面积的9倍?若存在,求点P的坐标;若不存在,请说明理由.
3.如图,二次函数y=x2+bx+c的图象过点B(0,1)、C(4,3)两点,与x轴交于点D、点E,过点B、C的直线与x轴交于点A.
(1)求二次函数的解析式;
(2)在x轴上有一动点P,随着点P的移动,存在点P使△PBC是直角三角形,请求出点P的坐标.
(3)若动点P在x轴上,动点Q在射线AC上,同时从A点出发,点P沿x轴正方向以每秒2个单位的速度运动,点Q以每秒a个单位的速度沿射线AC运动,是否存在以A、P、Q为顶点的三角形与△ABD相似,若存在,求a的值,若不存在,说明理由。
4.如图(1),直线y=−x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点M,使以C、P、M为顶点的三角形为等腰三角形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由;
(3)连结AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
5.在平面直角坐标系中,我们定义直线y=ax−a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
已知抛物线y=−x2−x+与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,
点A的坐标为 ,点B的坐标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
相关文档
- 数学文卷·2018届江西省上高二中高2021-04-17 23:43:5511页
- 专题12-2+机械波(押题专练)-2019年高2021-04-17 23:43:4616页
- 2017-2018学年四川省绵阳市南山中2021-04-17 23:43:408页
- 高中生物二轮复习专题练习2:遗传规2021-04-17 23:43:347页
- 中考数学模拟试题分类汇编压轴题含2021-04-17 23:43:2430页
- 2018_2019学年八年级数学上册第二2021-04-17 23:43:0361页
- 内蒙古师范大学锦山实验中学2019--2021-04-17 23:42:5812页
- 高考数学复习专题练习第7讲 函数2021-04-17 23:42:538页
- 2019-2020学年辽宁省实验中学东戴2021-04-17 23:42:4410页
- 湖北省松滋市一中2019-2020学年高2021-04-17 23:42:3924页