- 774.00 KB
- 2021-04-17 发布
绝密★启用前
2017-2018 学年度第一学期期中考试卷
高二数学(理科)
考试时间:120 分钟;满分 150 分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第 I 卷(选择题; 共 60 分)
一、选择题(共 12 题,每题 5 分共 60 分)
1.如图所示,观察四个几何体,其中判断正确的是( ).
A.(1)是棱台 B.(2)是圆台 C.(3)是棱锥 D.(4)不是棱柱
2.如果直线 a⊂平面α,直线 b⊂平面α,M∈a,N∈b,M∈l,N∈l,则( )
A.l⊂α B.l⊄α
C.l∩α=M D.l∩α=N
3.已知向量 =(1,x,-3), =(2,4,y),且 // ,那么 x+y 等于( )
A. -4 B. -2 C. 2 D. 4
4. 为空间任意一点,若 ,则 四点 ( )
A. 一定不共面 B. 一定共面 C. 不一定共面 D. 无法判断
5.长方体的一个顶点上三条棱的长分别是 3、4、5,且它的八个顶点都在同一个球面上,
则这个球的表面积是( )
A.π B.25π C.50π D.200π
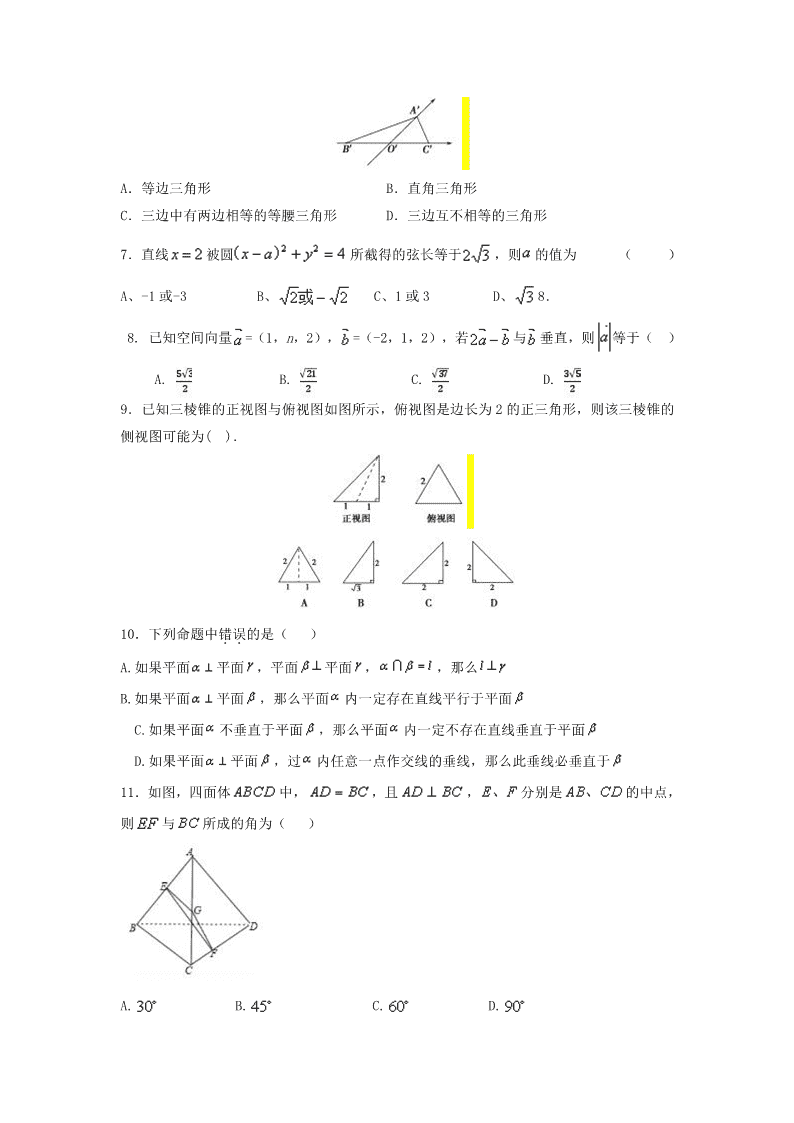
6.已知水平放置的△ABC 是按“斜二测画法”得到如右图所示的直观图,其中 B′O′=C′
O′=1,A′O′=
3
2,那么原△ABC 是一个( ).
A.等边三角形 B.直角三角形
C.三边中有两边相等的等腰三角形 D.三边互不相等的三角形
7.直线 被圆 所截得的弦长等于 ,则 的值为 ( )
A、-1 或-3 B、 C、1 或 3 D、 8.
8. 已知空间向量 =(1,n,2), =(-2,1,2),若 与 垂直,则 等于( )
A. B. C. D.
9.已知三棱锥的正视图与俯视图如图所示,俯视图是边长为 2 的正三角形,则该三棱锥的
侧视图可能为( ).
10.下列命题中错误..的是( )
A.如果平面 平面 ,平面 平面 , ,那么
B.如果平面 平面 ,那么平面 内一定存在直线平行于平面
C.如果平面 不垂直于平面 ,那么平面 内一定不存在直线垂直于平面
D.如果平面 平面 ,过 内任意一点作交线的垂线,那么此垂线必垂直于
11.如图,四面体 中, ,且 , 分别是 的中点,
则 与 所成的角为( )
A. B. C. D.
12.圆 上的点到直线 的最大距离与最小距离的差是
A.36 B. 18 C. D.
第 II 卷(非选择题 ;共 90 分)
二、填空题(共 4 题,每题 5 分共 20 分)
13 . 已 知 , 点 在 轴 上 , 且 , 则 点 的 坐 标 为
____________.
14.长方体 中, ,则 与平面 所
成的角的大小为
15.已知在长方 ABCD 中, ,点 是边 上的中点,则 __________.
16.如图所示,正方体 的棱长为 1,
分 别 是 棱 的 中 点 , 过 直 线 的 平 面 分 别 与 棱
交于 ,恰出以下四个命题:
① 平 面 一 定 为 矩 形 ; ② 平 面 平 面
;
③当 为 的中点时, 的面积最小;
④四棱锥 的体积为常数.
以上命题中正确命题的序号为__________.
三、解答题(共 6 题,70 分)
17.某个几何体的三视图如图所示(单位:m),
(1)求该几何体的表面积(结果保留π);
(2)求该几何体的体积(结果保留π).
18.已知圆经过 两点,并且圆心在直线 上。
(1)求圆的方程;
(2)求圆上的点到直线 的最小距离。
19.已知曲线是与两个定点 A(-4,0),B(2,0)距离比为 2 的点的轨迹,求此曲线的
方程
20.如图,在正三棱柱 ABC-A1B1C1 中,F,F1 分别是 AC,A1C1 的中点.
求证:(1)平面 AB1F1∥平面 C1BF;
(2)平面 AB1F1⊥平面 ACC1A1.
21.在直三棱柱 中, ∠ACB=90°
M是 的中点,N是 的中点。
(1)求证:MN∥平面 ;
(2)求点 到平面 BMC 的距离。
22.如图,ABCD 是边长为 3 的正方形,DE⊥平面 ABCD,AF∥DE,DE=3AF, BE
与平面 ABCD 所成角为 60°.
(Ⅰ)求证:AC⊥平面 BDE;(Ⅱ)求二面角 F-BE-D 的余弦值;
(Ⅲ)设点 M 是线段 BD 上一个动点,试确定点 M 的位置,使得 AM∥平面 BEF,
并证明你的结论.
2017-2018 学年度第一学期期中考试卷
高二数学(理科)答案
一、选择题:1-5CAABC 6-10ACDCD 11-12BC
二、填空题:13 0 0 3,, . 14.
6
15. 4 16.②③④
三、计算题:17 解 由三视图可知:该几何体的下半部分是棱长为 2 m 的正方体,上半部
分是半径为 1 m 的半球.
(1)几何体的表面积为 S=1
2
×4π×12+6×22-π×12=24+π(m2).
(2)几何体的体积为 V=23+1
2
×4
3
×π×13=8+2π
3 (m3).
18. 【解析】试题分析:(1)设出圆的一般方程,利用待定系数法求解;(2)结合几何图
形,先求出圆心到直线的距离,再减去半径的长度即可。
试题解析:
(1)设圆的方程为 2 2 0x y Dx Ey F ,
由已知条件有
2 2
2 2
2 5 2 5 0
{ 2 1 2 0
1
2 2 2
D E F
D E F
E D
,
解得
4
{ 2
11
D
E
F
所以圆的方程为 2 2 4 2 11 0,x y x y
2 22 1 16x y 即 .
(2)由(1)知,圆的圆心为 2,1 ,半径 r=4,
所以圆心到直线3 4 23 0x y 的距离 22
3 2 4 1 23 5
3 4
d
则圆上点到直线3 4 23 0x y 的最小距离为 1d r 。
19. 设 M(x,y)是曲线上任意点,点 M 在曲线上的条件是 MA
MB =2
则
2 2
2 2
( 4)
( 2)
x y
x y
=2
整理得(x-4) 2 +y 2 =16
所求曲线是圆心为(4,0),半径为 4 的圆
.20. 证明:(1)在正三棱柱 ABC-A1B1C1 中,
∵F,F1 分别是 AC,A1C1 的中点,
∴B1F1∥BF,AF1∥C1F.
又∵B1F1∩AF1=F1,C1F∩BF=F,
∴平面 AB1F1∥平面 C1BF.
(2)在正三棱柱 ABC-A1B1C1 中,AA1⊥平面 A1B1C1,
∴B1F1⊥AA1.
又 B1F1⊥A1C1,A1C1∩AA1=A1,
∴B1F1⊥平面 ACC1A1,而 B1F1⊂平面 AB1F1,
∴平面 AB1F1⊥平面 ACC1A1.
21. (1)如图所示,取 B1C1 中点 D,连结 ND、A1D
∴DN∥BB1∥AA1
又 DN= MAAABB 111 2
1
2
1
∴四边形 A1MND 为平行四边形。
∴MN∥A1 D 又 MN 平面 A1B1C1 AD1 平面 A1B1C1
∴MN∥平面 111 CBA --------------------------6 分
(2)因三棱柱 111 CBAABC 为直三棱柱, ∴C1 C ⊥BC,又∠ACB=90°
∴BC⊥平面 A1MC1
在平面 ACC1 A1 中,过 C1 作 C1H⊥CM,又 BC⊥C1H,故 C1H 为 C1 点到
平面 BMC 的距离。
在等腰三角形 CMC1 中,C1 C=2 2 ,CM=C1M= 6
∴
3
341
1
CM
ACCCHC .--------------------------8 分
22. (1)证明 ∵DE⊥平面 ABCD,∴DE⊥AC,∵四边形 ABCD 是正方形,
∴AC⊥BD,又 DE∩BD=D,
∴AC⊥平面 BDE.
(2)解 DE⊥平面 ABCD,
∴∠EBD 就是 BE 与平面 ABCD 所成的角,即∠EBD=60°.
∴ = .由 AD=3,得 BD=3 ,DE=3 ,AF= .
如图,分别以 DA,DC,DE 所在直线为 x 轴,y 轴,z 轴建立空间直角坐标系,则 A(3,0,0),F(3,0,
),E(0,0,3 ),B(3,3,0),C(0,3,0).
∴ =(0,-3, ), =(3,0,-2 ).
设平面 BEF 的法向量为 n=(x,y,z),则 即
令 z= ,则 n=(4,2, )
∵AC⊥平面 BDE,
∴ =(3,-3,0)为平面 BDE 的一个法向量,
∵cos〈n, 〉= = = ,
∴结合图形知二面角 F-BE-D 的余弦值为 .
(3)解 依题意,设 M(t,t,0)(0≤t<3),则 =(t-3,t,0),
∵AM∥平面 BEF,∴ ·n=0,
即 4(t-3)+2t=0,解得 t=2.
∴点 M 的坐标为(2,2,0),此时 = ,
∴点 M 是线段 BD 上靠近 B 点的三等分点