- 71.40 KB
- 2021-04-17 发布
第4.1.1节 圆的标准方程
1、情境设置:
在直角坐标系中,确定直线的基本要素是什么?圆作为平面几何中的基本图形,确定它的要素又是什么呢?什么叫圆?在平面直角坐标系中,任何一条直线都可用一个二元一次方程来表示,那么,原是否也可用一个方程来表示呢?如果能,这个方程又有什么特征呢?
探索研究:
2、探索研究:
确定圆的基本条件为圆心和半径,设圆的圆心坐标为A(a,b),半径为r。(其中a、b、r都是常数,r>0)设M(x,y)为这个圆上任意一点,那么点M满足的条件是(引导学生自己列出)P={M||MA|=r},由两点间的距离公式让学生写出点M适合的条件 ①
化简可得: ②
引导学生自己证明为圆的方程,得出结论。
方程②就是圆心为A(a,b),半径为r的圆的方程,我们把它叫做圆的标准方程。
3、知识应用与解题研究
例(1):写出圆心为半径长等于5的圆的方程,并判断点是否在这个圆上。
分析探求:可以从计算点到圆心的距离入手。
探究:点与圆的关系的判断方法:
(1)>,点在圆外
(2)=,点在圆上
(3)<,点在圆内
例(2):的三个顶点的坐标是求它的外接圆的方程
师生共同分析:从圆的标准方程 可知,要确定圆的标准方程,可用待定系数法确定三个参数.(学生自己运算解决)
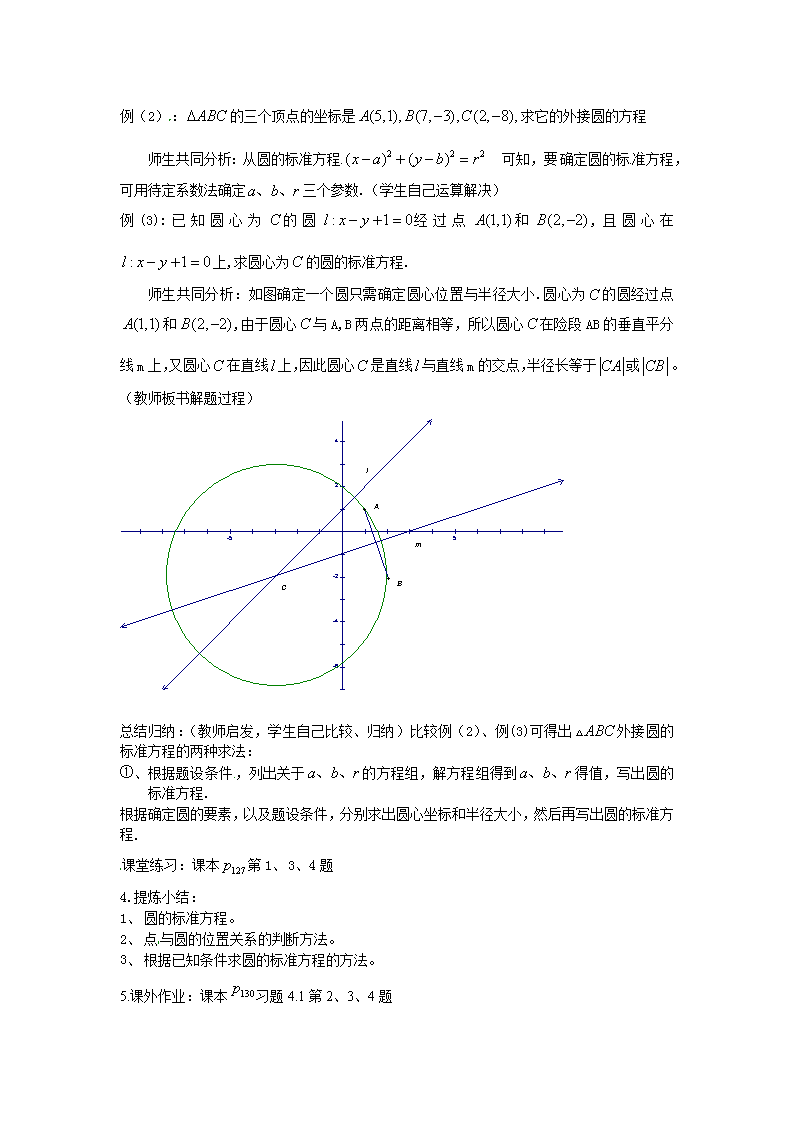
例(3):已知圆心为的圆经过点和,且圆心在上,求圆心为的圆的标准方程.
师生共同分析:如图确定一个圆只需确定圆心位置与半径大小.圆心为的圆经过点和,由于圆心与A,B两点的距离相等,所以圆心在险段AB的垂直平分线m上,又圆心在直线上,因此圆心是直线与直线m的交点,半径长等于或。
(教师板书解题过程)
总结归纳:(教师启发,学生自己比较、归纳)比较例(2)、例(3)可得出外接圆的标准方程的两种求法:
①、 根据题设条件,列出关于的方程组,解方程组得到得值,写出圆的标准方程.
根据确定圆的要素,以及题设条件,分别求出圆心坐标和半径大小,然后再写出圆的标准方程.
课堂练习:课本第1、3、4题
4.提炼小结:
1、 圆的标准方程。
2、 点与圆的位置关系的判断方法。
3、 根据已知条件求圆的标准方程的方法。
5.课外作业:课本习题4.1第2、3、4题
相关文档
- 2020高中语文散文部分第一单元那一2021-04-17 20:27:0383页
- 部编人教版语文八年级上册第12课《2021-04-17 20:26:591页
- 2019七年级数学下册 第5章5命题与2021-04-17 20:26:442页
- (山西专版)八年级语文上册专题九文言2021-04-17 20:26:3640页
- 高考数学 热点专题专练 专题五 数2021-04-17 20:26:3110页
- 江西省抚州市南城县第二中学2019-22021-04-17 20:26:2618页
- 2020九年级语文上册 第二单元 6 敬2021-04-17 20:26:227页
- 一年级上册数学课件- 10以内数的加2021-04-17 20:26:1716页
- 2020七年级数学上册截面与三视图讲2021-04-17 20:26:177页
- 2019届高考政治一轮复习人教版必修2021-04-17 20:26:076页