- 512.50 KB
- 2021-04-17 发布
数学
注意:1.请把答案填写在答题卡上,否则答题无效.
2.选择题,请用2B铅笔把答题卡上对应题目选项的信息涂黑。非选择题,请用0.5mm黑色签字笔在答题卡上指定位置作答.
第I卷(选择题,共60分)
一、 选择题:(本大题共12小题,每小题5分,共60分 .)
1.若点在角的终边上,则( )
A. B. C. D.
2.已知,,那么是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.将三进制数转化为十进制数,下列选项中正确的是( )
A.68 B.69 C.70 D.71
4.某校有男生人,女生人,现用分层抽样的方法从全校学生中抽取一个容量为的样本,则抽出的男生人数是( )
A. B. C. D.
5.已知某班有学生60人,现将所有学生按照0,1,2,…,59随机编号,若采用系统抽样的方法抽取一个容量为4的样本,且编号为2,32,47的学生在样本中,则样本中还有一个学生的编号为( )
A.26 B.23 C.17 D.13
6.从甲、乙、丙、丁四人中选取两人参加某项活动,则甲、乙两人有且仅有一人入选的概率为( )
A. B. C. D.
7.已知扇形的圆心角为,周长为,则扇形的面积为( )
A. B. C. D.
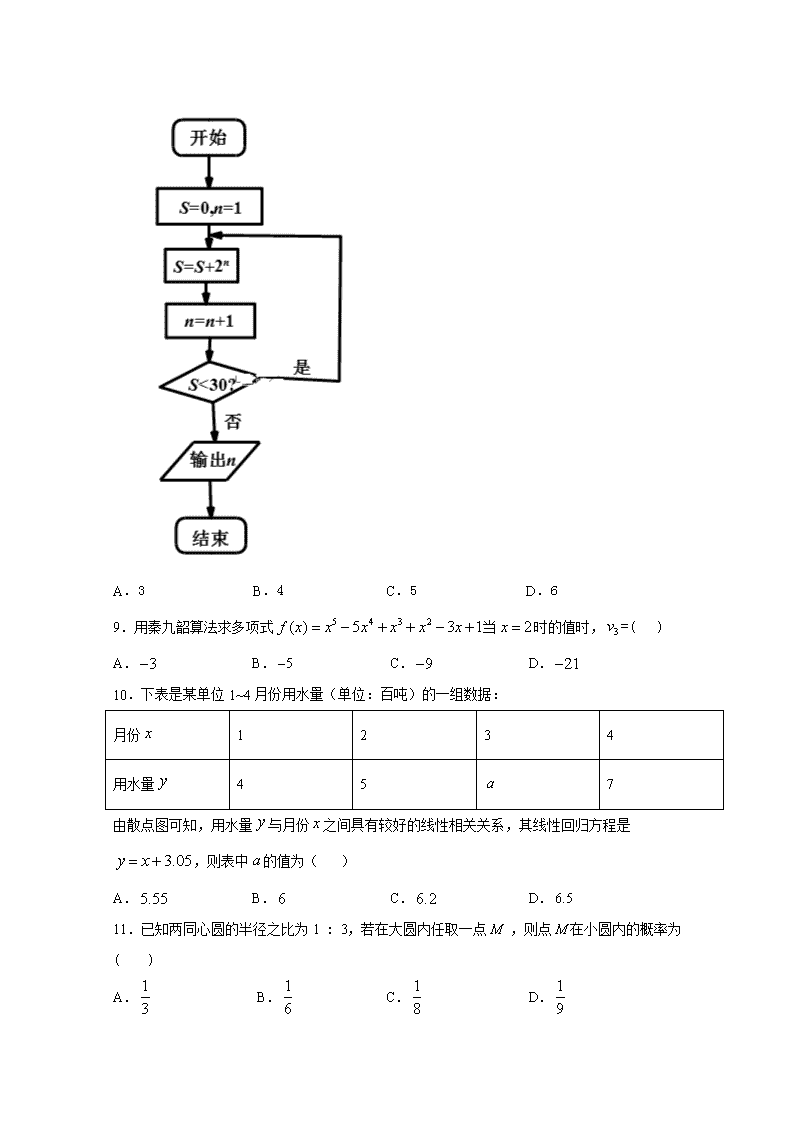
8.执行如图所示的程序框图,则输出的( )
A.3 B.4 C.5 D.6
9.用秦九韶算法求多项式当时的值时,=( )
A. B. C. D.
10.下表是某单位1~4月份用水量(单位:百吨)的一组数据:
月份
1
2
3
4
用水量
4
5
7
由散点图可知,用水量与月份之间具有较好的线性相关关系,其线性回归方程是,则表中的值为( )
A. B. C. D.
11.已知两同心圆的半径之比为1 : 3,若在大圆内任取一点M ,则点M在小圆内的概率为( )
A. B. C. D.
12.同时投掷两枚硬币一次,互斥而不对立的两个事件是( )
A.“至少有1枚正面朝上”与“2枚都是反面朝上”
B.“至少有1枚正面朝上”与“至少有1枚反面朝上”
C.“恰有1枚正面朝上”与“2枚都是正面朝上”
D.“至少有1枚反面朝上”与“2枚都是反面朝上”
第II卷(非选择题,共90分)
二.填空题(共20分,每小题5分)
13.72和168的最大公约数是______.
14.已知,则的值是__________.
15.已知,则的值等于______.
16.从编号为,,,的张卡片中随机抽取一张,放回后再随机抽取一张,则第二次抽得的卡片上的数字能被第一次抽得的卡片上数字整除的概率为_____________.
三.解答题(共70分)
17.(10分)求下列各式的值:
(1);
(2).
18(12分).已知,.
(1)求的值;
(2)求的值.
19.(12分)某赛季,甲、乙两名篮球运动员都参加了场比赛,他们所有比赛得分的情况如下:
甲:; 乙: .
(1) 求甲、乙两名运动员得分的中位数.
(2)分别求甲、乙两名运动员得分的平均数、方差,你认为哪位运动员的成绩更稳定?
20.(12分)某校某班在一次数学测验中,全班N
名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生有14人.
(1)求总人数N和分数在120~125的人数n;
(2)利用频率分布直方图,估算该班学生数学成绩的众数和中位数各是多少?
21.(12分)随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份
2013
2014
2015
2016
2017
时间代号
1
2
3
4
5
储蓄存款/千亿元
5
6
7
8
10
(1)求关于的线性回归方程;
(2)用所求回归方程预测该地区2019年的人民币储蓄存款.
(附: ,其中,为样本平均值)
22.(12分)从一个装有3个红球和2个白球的盒子中,随机取出2个球.
(1)用球的标号列出所有可能的取出结果;
(2)求取出的2个球都是红球的概率.
参考答案
1.B 2.C 3.B 4.A 5.C 6.B 7.B
设该扇形的半径为,弧长为,则,且,所以有,
所以,该扇形的面积为.
8.C
9.C 由题意得,,则当时,有,,.故选C.
10.C 由样本中心点满足线性回归方程求解即可.
解:由图表数据可得,,
又用水量与月份之间具有较好的线性相关关系,其线性回归方程是,
则, 则,
11.D 设小圆的半径为,则大圆的半径为,
所以小圆的面积为:,
大圆的面积为:.
所以点M在小圆内的概率为:.
12.C
在A中,“至少有1枚正面朝上”与“2枚都是反面朝上”不能同时发生,且“至少有1枚正面朝上”不发生时,“2枚都是反面朝上”一定发生,故A中的两个事件是对立事件;
在B中,当两枚硬币恰好1枚正面朝上,1枚反面朝上时,“至少有1枚正面朝上”与“至少有1枚反面朝上”能同时发生,故B中的两个事件不是互斥事件;
在C中,“恰有1枚正面朝上”与“2枚都是正面朝上”不能同时发生,且其中一个不发生时,另一个有可能发生也有可能不发生,故C中的两个事件是互斥而不对立事件;
在D中,当2枚硬币同时反面朝上时,“至少有1枚反面朝上”“2枚都是反面朝上”能同时发生,故D中的两个事件不是互斥事件.
13.24
14.
由,平方可得.
解得.
15.
,故答案为.
16.
17. 解:(1)原式
;
(2)原式.
18.
(1),,因此,;
(2)原式.
19.(1) 甲中位数是,乙中位数是;(2),,,,甲运动员的成绩更稳定.
(1)分别将甲、乙两名运动员得分的两组数据从大到小排列,找出中位数即可;
(2)按照定义分别计算甲、乙两名运动员得分的平均数、方差,通过方差比较甲、乙两名运动员的成绩即可.
【详解】
(1)将甲运动员得分的数据由大到小排列:.
将乙运动员得分的数据由大到小排列:.
甲运动员得分的中位数是,乙运动员得分的中位数是.
(2),
,
,
,
,
甲运动员的成绩更稳定.
【点睛】
本题考查中位数、平均数、方差的定义及应用,属于基础题.
20.(1);(2)众数,中位数.
解:(1)分数在110~120内的学生的频率为
,
所以该班总人数.
分数在120~125内的学生的频率为
,
分数在120~125内的人数.
(2)由频率分布直方图可知,众数是最高的小矩形底边中点的横坐标,
即为.
设中位数为,∵,
∴.
∴众数和中位数分别是107.5,110.
21.(1)(2)12
(1)根据题意得:,
,
,
,
,
,所以关于的线性回归方程
(2)当t=7时,y=1.2×7+3.6=12(千亿元).
22.
解:(1)随机取出2个球的可能的结果有:
;
(2)取出的2个球都是红球的结果有,
则取出的2个球都是红球的概率.
.