- 574.50 KB
- 2021-04-17 发布
定远中学2017-2018学年第一学期1月考
高二数学(文科)试题
注意事项:
1.答题前在答题卡、答案纸上填写好自己的姓名、班级、考号等信息
2.请将第I卷(选择题)答案用2B铅笔正确填写在答题卡上;请将第II卷(非选择题)答案黑色中性笔正确填写在答案纸上。
第I卷(选择题60分)
一、选择题(本大题共12个小题,每小题5分,共60分。)
1.若直线l:mx+ny=4和圆O:x2+y2=4没有交点,则过点(m,n)的直线与椭圆的交点个数为( )
A.0个 B.至多有一个 C.1个 D.2个
2.若直线过圆的圆心,则的最小值为( )
A.8 B.12 C.16 D.20
3.已知命题:方程有两个实数根;命题:函数的最小值为.给出下列命题:
①;②;③;④.
则其中真命题的个数为( )
A. B. C. D.
4.已知,命题“若,则”的否命题是( )
A.若,则
B.若,则
C.若,则
D.若,则
5.圆关于直线成轴对称图形,则的取值范围是( )
A. B.
C. D.
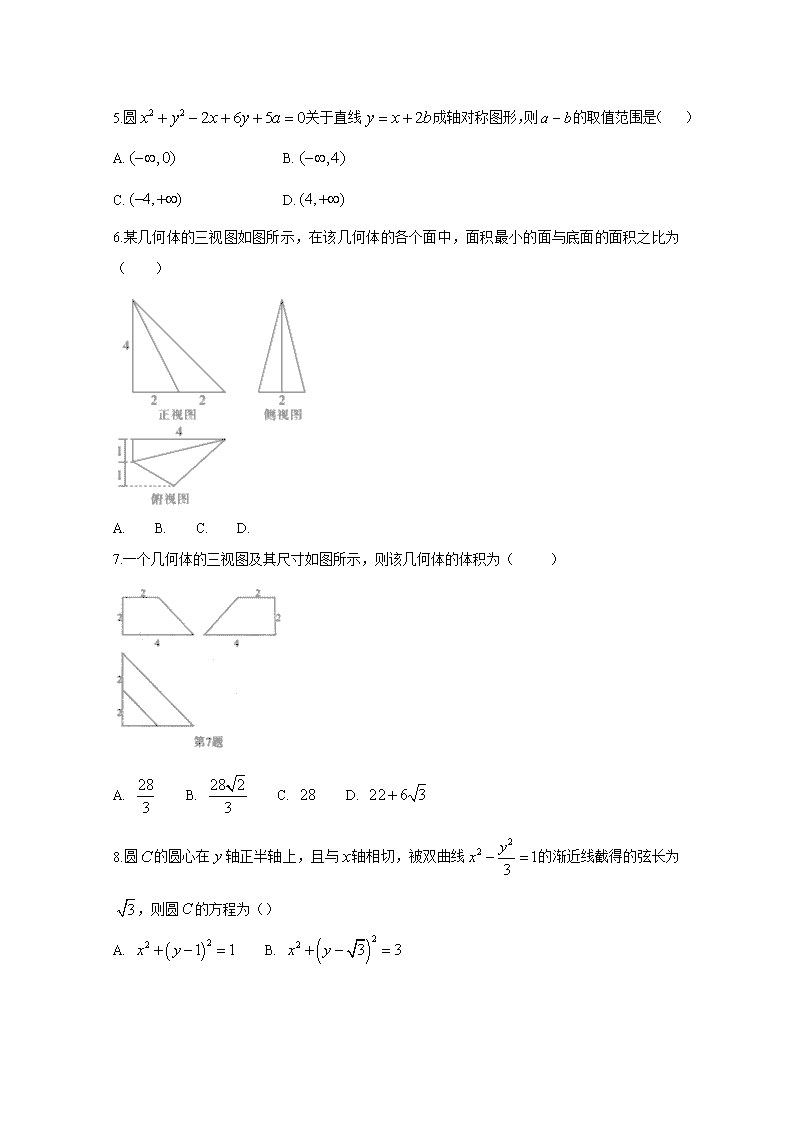
6.某几何体的三视图如图所示,在该几何体的各个面中,面积最小的面与底面的面积之比为( )
A. B. C. D.
7.一个几何体的三视图及其尺寸如图所示,则该几何体的体积为( )
A. B. C. D.
8.圆的圆心在轴正半轴上,且与轴相切,被双曲线的渐近线截得的弦长为,则圆的方程为()
A. B.
C. D.
9.在正方体中,点分别是的中点,则与所成角的大小为( )
A. B. C. D.
10.已知、是两条不同直线, 、、是三个不同平面,则下列正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
11.已知是两个不同平面,直线,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
12.把半径分别为的三个铁球熔成一个大铁球,这个大铁球的半径为 ( )
A. B. C. D.
第II卷(非选择题90分)
二、填空题(共4小题,每小题5分,共20分)
13.半径为2的球的内接几何体的三视图如图,则其体积为 .
14.已知命题函数在定义域上单调递增;命题不等式对任意实数恒成立.若是真命题,则实数的取值范围为_____________.
15.已知边长为的正的三个顶点都在球的表面上,且与平面所成的角为,则球的表面积为__________.
16.如图所示, 在直三棱柱中, 为的中点, 则 三棱锥的体积是_________.
三、解答题(共5小题, 每小题14分,共70分)
17.已知直角梯形ABCD的下底与等腰直角三角形ABE的斜边重合,AB⊥BC,且AB=2CD=2BC(如图1),将此图形沿AB折叠,使得平面ABE⊥平面ABCD,连接EC、ED,得到四棱锥E﹣ABCD(如图2).
(1)求证:在四棱锥E﹣ABCD中,AB⊥DE.
(2)设BC=1,求点C到平面EBD的距离.
18.如图所示的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).
(1)按照画三视图的要求画出该多面体的俯视图;
(2)在所给直观图中连接,求证:∥面.
19.如图,在三棱柱中,已知,.四边形为正方形,设的中点为D,
求证:(Ⅰ);
(Ⅱ).
20.如图所示,在三棱锥中,分别为的中点.
(1)证明: 平面;
(2)若求证:.
21.在平面直角坐标系xOy中,已知椭圆C:(m>0)的离心率为,A,B分别为椭圆的左、右顶点,F是其右焦点,P是椭圆C上异于A、B的动点.
(1)求m的值及椭圆的准线方程;
(2)设过点B且与x轴的垂直的直线交AP于点D,当直线AP绕点A转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.
参考答案
1. D2.C3.C4.A5.B6.C7.A8.A9.B10.D11.A12.D
13.
14.-2