2018届二轮复习专题四第1讲　立体几何中的计算与位置关系课件（全国通用） 49页

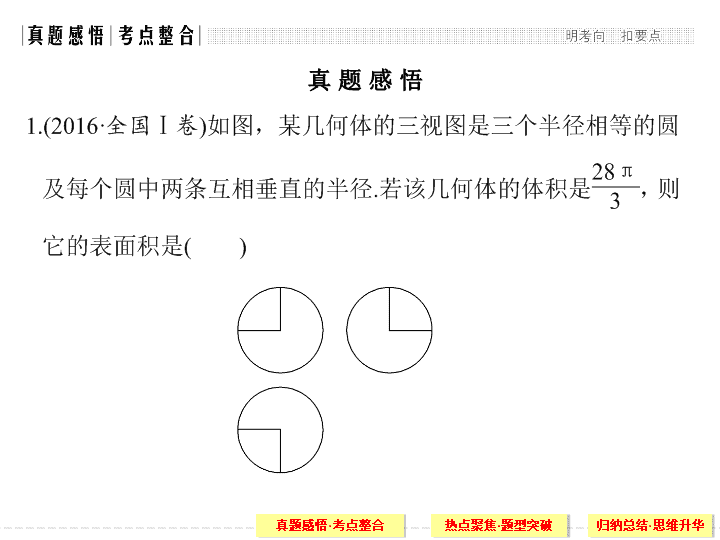
第 1 讲　立体几何中的计算与位置关系 高考定位　 1. 以三视图和空间几何体为载体考查面积与体积 ， 难度中档偏下； 2. 以选择题、填空题的形式考查线线、线面、面面位置关系的判定与性质定理对命题的真假进行判断 ， 属基础题；空间中的平行、垂直关系的证明也是高考必考内容 ，多出现在立体几何解答题中的第 ( 1) 问 . 真 题 感 悟 A.17 π B.18 π C.20 π D.28 π 答案　 A 2. (2015· 重庆卷 ) 某几何体的三视图如图所示，则该几何体的体积为 ( 　　 ) 答案　 A 3. (2016· 全国 Ⅲ 卷 ) 如图，网格纸上小正方形的边长为 1 ，粗实线画出的是某多面体的三视图，则该多面体的表面积为 ( 　　 ) 答案　 B 4. (2016· 全国 Ⅱ 卷 ) α ， β 是两个平面， m ， n 是两条直线，有下列四个命题： 答案 　 ②③④ 考 点 整 合 1. 四棱柱、直四棱柱、正四棱柱、正方体、平行六面体、直平行六面体、长方体之间的关系 . 2. 几何体的摆放位置不同，其三视图也不同，需要注意长对正，高平齐，宽相等 . 3. 空间几何体的两组常用公式 4. 直线、平面平行的判定及其性质 5. 直线、平面垂直的判定及其性质 热点一　空间几何体的表面积与体积的求解 [ 微题型 1] 　以三视图为载体求几何体的面积与体积 【例 1 － 1 】 (1) (2016· 衡水大联考 ) 如图，网格纸上小正方形的边长为 1 ，粗实线和虚线画出的是多面体的三视图，则该多面体的体积为 ( 　　 ) (2) 某三棱锥的三视图如图所示，该三棱锥的表面积是 ( 　　 ) 解析　 (1) 由图知此几何体为边长为 2 的正方体裁去一个三棱锥 . 答案　 (1)C 　 (2)B 探究提高 　 截割体、三棱锥的三视图是高考考查的热点和难点 ， 解题的关键是由三视图还原为直观图 ， 首先确定底面 ， 再根据正视图、侧视图确定侧面 . [ 微题型 2] 　求多面体的体积 【例 1 － 2 】 (1) 如图，在棱长为 6 的正方体 ABCD － A 1 B 1 C 1 D 1 中， E ， F 分别在 C 1 D 1 与 C 1 B 1 上，且 C 1 E ＝ 4 ， C 1 F ＝ 3 ，连接 EF ， FB ， DE ， BD 则几何体 EFC 1 － DBC 的体积为 ( 　　 ) A.66 B.68 C.70 D.72 (2) 如图，正方体 ABCD － A 1 B 1 C 1 D 1 的棱长为 1 ， E ， F 分别为线段 AA 1 ， B 1 C 上的点，则三棱锥 D 1 － EDF 的体积为 ________. 探究提高 　 (1) 求三棱锥的体积 ， 等体积转化是常用的方法 ， 转换原则是其高易求 ， 底面放在已知几何体的某一面上 . (2) 若所给的几何体的体积不能直接利用公式得出 ，则常用转换法、分割法、 补形法等方法求解 . [ 微题型 3] 　与球有关的面积、体积问题 【例 1 － 3 】 (1) 如图所示是一个几何体的三视图，则这个几何体外接球的表面积为 ( 　　 ) A.8 π 　　　 B.16 π C.32 π 　　　 D.64 π (2) 已知三棱锥 S － ABC 的所有顶点都在球 O 的球面上， △ ABC 是边长为 1 的正三角形， SC 为球 O 的直径，且 SC ＝ 2 ，则此三棱锥的体积为 ( 　　 ) 答案　 (1)C 　 (2)A 探究提高 　 涉及球与棱柱、棱锥的切、接问题时 ， 一般过球心及多面体中的特殊点 ( 一般为接、切点 ) 或线作截面 ， 把空间问题转化为平面问题 ， 再利用平面几何知识寻找几何体中元素间的关系 ，或只画内切、外接的几何体的直观图， 确定球心的位置 ，弄清球的半径 ( 直径 ) 与该几何体已知量的关系，列方程 ( 组 ) 求解 . 【训练 1 】 (1) (2017· 东营模拟 ) 某几何体的三视图如图所示，则该几何体的表面积为 ( 　　 ) A.54 B.60 C.66 D.72 (2) (2016· 北京卷 ) 某三棱锥的三视图如图所示，则该三棱锥的体积为 ( 　　 ) 答案　 (1)B 　 (2)A 热点二　空间中的平行与垂直 [ 微题型 1] 　空间线面位置关系的判断 【例 2 － 1 】 已知平面 α 、 β ，直线 m ， n ，给出下列命题： 答案　 ③④ 探究提高 　 长方体 ( 或正方体 ) 是一类特殊的几何体 ， 其中蕴含着丰富的空间位置关系 . 因此 ， 对于某些研究空间直线与直线、直线与平面、平面与平面之间的平行、垂直关系问题 ， 常构造长方体 ( 或正方体 ) ， 把点、线、面的位置关系转移到长方体 ( 或正方体 ) 中 ，对各条件进行检验或推理，根据条件在某一 特殊情况下不真 ，则它在一般情况下也不真的原理，判断条件的真伪，可使此类问题迅速获解 . [ 微题型 2] 　平行、垂直关系的证明 探究提高 　 垂直、平行关系证明中应用转化与化归思想的常见类型 . (1) 证明线面、面面平行 ， 需转化为证明线线平行 . (2) 证明线面垂直 ， 需转化为证明线线垂直 . (3) 证明线线垂直 ， 需转化为证明线面垂直 . (4) 证明面面垂直 ， 需转化为证明线面垂直 ， 进而转化为证明线线垂直 . 图 1 图 2 1. 求解几何体的表面积或体积 (1) 对于规则几何体，可直接利用公式计算 . (2) 对于不规则几何体，可采用割补法求解；对于某些三棱锥，有时可采用等体积转换法求解 . (3) 求解旋转体的表面积和体积时，注意圆柱的轴截面是矩形，圆锥的轴截面是等腰三角形，圆台的轴截面是等腰梯形的应用 . (4) 求解几何体的表面积时要注意 S 表 ＝ S 侧 ＋ S 底 . 4. 空间中点、线、面的位置关系的判定 (1) 可以从线、面的概念、定理出发，学会找特例、反例 . (2) 可以借助长方体，在理解空间点、线、面位置关系的基础上，抽象出空间线、面的位置关系的定义 . 5. 垂直、平行关系的基础是线线垂直和线线平行，常用方法如下： 6. 解决平面图形的翻折问题，关键是抓住平面图形翻折前后的不变 “ 性 ” 与 “ 量 ” ，即两条直线的平行与垂直关系以及相关线段的长度、角度等 .