2019年高考数学高分突破复习课件专题三 第3讲 51页

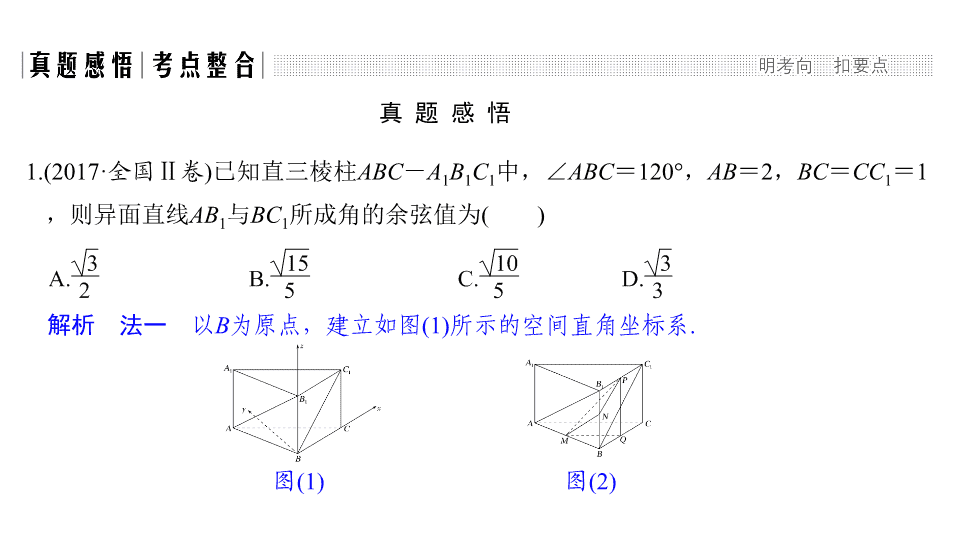
第 3 讲　立体几何中的向量方法 高考定位　 以空间几何体为载体考查空间角是高考命题的重点，常与空间线面关系的证明相结合，热点为二面角的求解，均以解答题的形式进行考查，难度主要体现在建立空间直角坐标系和准确计算上 . 1. (2017· 全国 Ⅱ 卷 ) 已知直三棱柱 ABC － A 1 B 1 C 1 中， ∠ ABC ＝ 120° ， AB ＝ 2 ， BC ＝ CC 1 ＝ 1 ，则异面直线 AB 1 与 BC 1 所成角的余弦值为 ( 　　 ) 解析 　 法一 　 以 B 为原点，建立如图 (1) 所示的空间直角坐标系 . 真 题 感 悟 图 (1 ) 　　　　　　　　　　图 (2) 则 B (0 ， 0 ， 0) ， B 1 (0 ， 0 ， 1) ， C 1 (1 ， 0 ， 1). 法二 　 如图 (2) ，设 M ， N ， P 分别为 AB ， BB 1 ， B 1 C 1 中点，则 PN ∥ BC 1 ， MN ∥ AB 1 ， ∴ AB 1 与 BC 1 所成的角是 ∠ MNP 或其补角 . ∵ AB ＝ 2 ， BC ＝ CC 1 ＝ 1 ， 在 △ ABC 中， AC 2 ＝ AB 2 ＋ BC 2 － 2 AB · BC ·cos ∠ ABC 答案 　 C (1) 证明：平面 AMD ⊥ 平面 BMC ； (2) 当三棱锥 M － ABC 体积最大时，求平面 MAB 与平面 MCD 所成二面角的正弦值 . (1) 证明　 由题设知，平面 CMD ⊥ 平面 ABCD ，交线为 CD . 因为 BC ⊥ CD ， BC ⊂ 平面 ABCD ， 所以 BC ⊥ 平面 CMD ，又 DM ⊂ 平面 CDM ，故 BC ⊥ DM . 所以 DM ⊥ CM . 又 BC ∩ CM ＝ C ，所以 DM ⊥ 平面 BMC . 由于 DM ⊂ 平面 AMD ，故平面 AMD ⊥ 平面 BMC . 由题设得 D (0 ， 0 ， 0) ， A (2 ， 0 ， 0) ， B (2 ， 2 ， 0) ， C (0 ， 2 ， 0) ， M (0 ， 1 ， 1) ， 设 n ＝ ( x ， y ， z ) 是平面 MAB 的法向量， 3. (2018· 全国 Ⅰ 卷 ) 如图，四边形 ABCD 为正方形， E ， F 分别为 AD ， BC 的中点，以 DF 为折痕把 △ DFC 折起，使点 C 到达点 P 的位置，且 PF ⊥ BF . ( 1) 证明：平面 PEF ⊥ 平面 ABFD ； ( 2) 求 DP 与平面 ABFD 所成角的正弦值 . (1) 证明　 由已知可得， BF ⊥ PF ， BF ⊥ EF ， 又 PF ∩ EF ＝ F ， PF ， EF ⊂ 平面 PEF ，所以 BF ⊥ 平面 PEF . 又 BF ⊂ 平面 ABFD ，所以平面 PEF ⊥ 平面 ABFD . (2) 解　 作 PH ⊥ EF ，垂足为 H . 由 (1) 得， PH ⊥ 平面 ABFD . 由 (1) 可得， DE ⊥ PE . 又 DP ＝ 2 ， DE ＝ 1 ， 1. 直线与平面、平面与平面的平行与垂直的向量方法 设直线 l 的方向向量为 a ＝ ( a 1 ， b 1 ， c 1 ) ，平面 α ， β 的法向量分别为 μ ＝ ( a 2 ， b 2 ， c 2 ) ， v ＝ ( a 3 ， b 3 ， c 3 ) ，则 (1) 线面平行 l ∥ α ⇔ a ⊥ μ ⇔ a · μ ＝ 0 ⇔ a 1 a 2 ＋ b 1 b 2 ＋ c 1 c 2 ＝ 0. (2) 线面垂直 l ⊥ α ⇔ a ∥ μ ⇔ a ＝ k μ ⇔ a 1 ＝ ka 2 ， b 1 ＝ kb 2 ， c 1 ＝ kc 2 . (3) 面面平行 α ∥ β ⇔ μ ∥ v ⇔ μ ＝ λ v ⇔ a 2 ＝ λa 3 ， b 2 ＝ λb 3 ， c 2 ＝ λc 3 . (4) 面面垂直 α ⊥ β ⇔ μ ⊥ v ⇔ μ · v ＝ 0 ⇔ a 2 a 3 ＋ b 2 b 3 ＋ c 2 c 3 ＝ 0. 考 点 整 合 2. 直线与直线、直线与平面、平面与平面的夹角计算 设直线 l ， m 的方向向量分别为 a ＝ ( a 1 ， b 1 ， c 1 ) ， b ＝ ( a 2 ， b 2 ， c 2 ) ，平面 α ， β 的法向量分别为 μ ＝ ( a 3 ， b 3 ， c 3 ) ， v ＝ ( a 4 ， b 4 ， c 4 )( 以下相同 ). 热点一　利用空间向量证明平行、垂直关系 【例 1 】 如图，在四棱锥 P － ABCD 中， PA ⊥ 底面 ABCD ， AD ⊥ AB ， AB ∥ DC ， AD ＝ DC ＝ AP ＝ 2 ， AB ＝ 1 ，点 E 为棱 PC 的中点 . 证明： (1) BE ⊥ DC ； (2) BE ∥ 平面 PAD ； (3) 平面 PCD ⊥ 平面 PAD . 证明 　依题意，以点 A 为原点建立空间直角坐标系 ( 如图 ) ， 可得 B (1 ， 0 ， 0) ， C (2 ， 2 ， 0) ， D (0 ， 2 ， 0) ， P (0 ， 0 ， 2 ). 由 E 为棱 PC 的中点，得 E (1 ， 1 ， 1). (2) 因为 AB ⊥ AD ，又 PA ⊥ 平面 ABCD ， AB ⊂ 平面 ABCD ， 所以 AB ⊥ PA ， PA ∩ AD ＝ A ， PA ， AD ⊂ 平面 PAD ， 所以 AB ⊥ 平面 PAD ， 又 BE ⊄ 平面 PAD ，所以 BE ∥ 平面 PAD . 设平面 PCD 的一个法向量为 n ＝ ( x ， y ， z ) ， 不妨令 y ＝ 1 ，可得 n ＝ (0 ， 1 ， 1) 为平面 PCD 的一个法向量 . 所以平面 PAD ⊥ 平面 PCD . 探究提高　 1. 利用向量法证明平行、垂直关系，关键是建立恰当的坐标系 ( 尽可能利用垂直条件，准确写出相关点的坐标，进而用向量表示涉及到直线、平面的要素 ). 2. 向量证明的核心是利用向量的数量积或数乘向量，但向量证明仍然离不开立体几何定理的条件，如在 (2) 中忽略 BE ⊄ 平面 PAD 而致误 . 【训练 1 】 在直三棱柱 ABC － A 1 B 1 C 1 中， ∠ ABC ＝ 90° ， BC ＝ 2 ， CC 1 ＝ 4 ，点 E 在线段 BB 1 上，且 EB 1 ＝ 1 ， D ， F ， G 分别为 CC 1 ， C 1 B 1 ， C 1 A 1 的中点 . 求证： ( 1) B 1 D ⊥ 平面 ABD ； ( 2) 平面 EGF ∥ 平面 ABD . 证明 　 (1) 以 B 为坐标原点， BA ， BC ， BB 1 所在的直线分别为 x 轴、 y 轴、 z 轴，建立空间直角坐标系，如图所示 . 则 B (0 ， 0 ， 0) ， D (0 ， 2 ， 2) ， B 1 (0 ， 0 ， 4) ， C 1 (0 ， 2 ， 4). 设 BA ＝ a ，则 A ( a ， 0 ， 0) ， 则 B 1 D ⊥ BA ， B 1 D ⊥ BD . 又 BA ∩ BD ＝ B ， BA ， BD ⊂ 平面 ABD ， 因此 B 1 D ⊥ 平面 ABD . 即 B 1 D ⊥ EG ， B 1 D ⊥ EF . 又 EG ∩ EF ＝ E ， EG ， EF ⊂ 平面 EGF ， 因此 B 1 D ⊥ 平面 EGF . 结合 (1) 可知平面 EGF ∥ 平面 ABD . 热点二　利用空间向量计算空间角 考法 1 　求线面角或异面直线所成的角 【例 2 － 1 】 (2018· 烟台质检 ) 如图，在梯形 ABCD 中， AD ＝ BC ， AB ∥ CD ， AC ⊥ BD ，平面 BDFE ⊥ 平面 ABCD ， EF ∥ BD ， BE ⊥ BD . (1) 证明　 ∵ 平面 BDFE ⊥ 平面 ABCD ，平面 BDFE ∩ 平面 ABCD ＝ BD ， AC ⊂ 平面 ABCD ， AC ⊥ BD ， ∴ AC ⊥ 平面 BDFE . 又 AC ⊂ 平面 AFC ， ∴ 平面 AFC ⊥ 平面 BDFE . ∴ OD ＝ OC ＝ 1 ， OB ＝ OA ＝ 2 ， ∵ FE ∥ OB 且 FE ＝ OB ， ∴ 四边形 FEBO 为平行四边形， ∴ OF ∥ BE ，且 OF ＝ BE ＝ 2 ， 又 ∵ BE ⊥ 平面 ABCD ， ∴ OF ⊥ 平面 ABCD . 则 B (0 ， 2 ， 0) ， D (0 ，－ 1 ， 0) ， F (0 ， 0 ， 2) ， C ( － 1 ， 0 ， 0) ， 不妨设 z ＝ 1 ，得 x ＝ y ＝－ 2 ，得 n ＝ ( － 2 ，－ 2 ， 1). 探究提高　 1. 异面直线所成的角 θ ，可以通过两直线的方向向量的夹角 φ 求得，即 cos θ ＝ |cos φ |. 2. 直线与平面所成的角 θ 主要通过直线的方向向量与平面的法向量的夹角 φ 求得，即 sin θ ＝ |cos φ | ，有时也可分别求出斜线与它在平面内的射影直线的方向向量，转化为求两方向向量的夹角 ( 或其补角 ). 【训练 2 】 (2018· 江苏卷 ) 如图，在正三棱柱 ABC － A 1 B 1 C 1 中， AB ＝ AA 1 ＝ 2 ，点 P ， Q 分别为 A 1 B 1 ， BC 的中点 . ( 1) 求异面直线 BP 与 AC 1 所成角的余弦值； ( 2) 求直线 CC 1 与平面 AQC 1 所成角的正弦值 . 因为 AB ＝ AA 1 ＝ 2 ， 设 n ＝ ( x ， y ， z ) 为平面 AQC 1 的一个法向量， (1) 证明： BC ⊥ B 1 M ； (2) 若平面 MB 1 C 把此棱柱分成体积相等的两部分，求此时二面角 M － B 1 C － A 的余弦值 . ∴ BC ＝ 2 ，则有 AB 2 ＋ BC 2 ＝ 8 ＝ AC 2 ， ∴∠ ABC ＝ 90° ， ∴ BC ⊥ AB ， 又 ∵ BB 1 ⊥ BC ， BB 1 ∩ AB ＝ B ， ∴ BC ⊥ 平面 ABB 1 A 1 ，又 B 1 M ⊂ 平面 ABB 1 A 1 ， 故 BC ⊥ B 1 M . (2) 解　 由题设知，平面 MB 1 C 把此三棱柱分成两个体积相等的几何体为四棱锥 C － ABB 1 M 和四棱锥 B 1 － A 1 MCC 1 . 由 (1) 知四棱锥 C － ABB 1 M 的高为 BC ＝ 2 ， 此时 M 为 AA 1 中点， ∴ A (2 ， 0 ， 0) ， C (0 ， 2 ， 0) ， B 1 (0 ， 0 ， 4) ， M (2 ， 0 ， 2). 设 n 1 ＝ ( x 1 ， y 1 ， z 1 ) 是平面 CB 1 M 的一个法向量， 令 z 1 ＝ 1 ，可得 n 1 ＝ (1 ， 2 ， 1) ，设 n 2 ＝ ( x 2 ， y 2 ， z 2 ) 是平面 ACB 1 的一个法向量 ， 探究提高　 1. 二面角的大小可以利用分别在两个半平面内与棱垂直的直线的方向向量的夹角 ( 或其补角 ) 或通过二面角的两个面的法向量的夹角求得，它等于两个法向量的夹角或其补角 . 2. 利用向量法求二面角，必须能判定 “ 所求二面角的平面角是锐角或钝角 ” ，否则解法是不严谨的 . (1) 求证： AC ⊥ 平面 BEF ； (2) 求二面角 B － CD － C 1 的余弦值； (3) 证明：直线 FG 与平面 BCD 相交 . (1) 证明 　在三棱柱 ABC － A 1 B 1 C 1 中， 因为 CC 1 ⊥ 平面 ABC ， 所以四边形 A 1 ACC 1 为矩形 . 又 E ， F 分别为 AC ， A 1 C 1 的中点 ，所以 AC ⊥ EF . 因为 AB ＝ BC ，所以 AC ⊥ BE . 又 EF ∩ BE ＝ E ，所以 AC ⊥ 平面 BEF . (2) 解 　由 (1) 知 AC ⊥ EF ， AC ⊥ BE ， EF ∥ CC 1 ， 又 CC 1 ⊥ 平面 ABC ，所以 EF ⊥ 平面 ABC ， 因为 BE ⊂ 平面 ABC ，所以 EF ⊥ BE . 如图建立空间直角坐标系 E － xyz ，由题意得 B (0 ， 2 ， 0) ， C ( － 1 ， 0 ， 0) ， D (1 ， 0 ， 1) ， F (0 ， 0 ， 2) ， G (0 ， 2 ， 1). 设平面 BCD 的法向量为 n ＝ ( x 0 ， y 0 ， z 0 ) ， 令 y 0 ＝－ 1 ，则 x 0 ＝ 2 ， z 0 ＝－ 4 . 于是 n ＝ (2 ，－ 1 ，－ 4). 所以直线 FG 与平面 BCD 相交 . 解　 (1) 设 BD 交 AC 于点 O ，连接 OE . ∵ PB ∥ 平面 AEC ，平面 AEC ∩ 平面 BDP ＝ OE ， ∴ PB ∥ OE . 又 O 为 BD 的中点， ∴ 在 △ BDP 中 E 为 PD 中点 . (2) 连接 OP ，由题知 PO ⊥ 平面 ABCD ，且 AC ⊥ BD ， 设平面 AEC 的法向量为 m ＝ ( x 1 ， y 1 ， z 1 ). 设平面 BDF 的法向量 n ＝ ( x 2 ， y 2 ， z 2 ) ， 探究提高　 1. 空间向量最适合于解决立体几何中的探索性问题，它无需进行复杂的作图、论证、推理，只需通过坐标运算进行判断 . 2. 空间向量求解探索性问题： (1) 假设题中的数学对象存在 ( 或结论成立 ) 或暂且认可其中的一部分结论； (2) 在这个前提下进行逻辑推理，把要成立的结论当作条件，据此列方程或方程组，把 “ 是否存在 ” 问题转化为 “ 点的坐标 ( 或参数 ) 是否有解，是否有规定范围内的解 ” 等 . 若由此推导出矛盾，则否定假设；否则，给出肯定结论 . (1) 当 BF 长为多少时，平面 AEF ⊥ 平面 CEF? (2) 在 (1) 的条件下，求二面角 E － AC － F 的余弦值 . 解　 (1) 连接 BD 交 AC 于点 O ，则 AC ⊥ BD . 取 EF 的中点 G ，连接 OG ，则 OG ∥ DE . ∵ DE ⊥ 平面 ABCD ， ∴ OG ⊥ 平面 ABCD . ∴ OG ， AC ， BD 两两垂直 . 以 AC ， BD ， OG 所在直线分别作为 x 轴， y 轴， z 轴建立空间直角坐标系 ( 如图 ) ， 设平面 AEF ，平面 CEF 的法向量分别为 n 1 ＝ ( x 1 ， y 1 ， z 1 ) ， n 2 ＝ ( x 2 ， y 2 ， z 2 ). 若平面 AEF ⊥ 平面 CEF ，则 n 1 · n 2 ＝ 0 ， 设平面 AEC 的一个法向量为 n ＝ ( x ， y ， z ) ，则 3. 利用空间向量求解二面角时，易忽视二面角的范围，误以为两个法向量的夹角就是所求的二面角，导致出错 . 4. 空间向量在处理空间问题时具有很大的优越性，能把 “ 非运算 ” 问题 “ 运算 ” 化，即通过直线的方向向量和平面的法向量，把立体几何中的平行、垂直关系，各类角、距离以向量的方式表达出来，把立体几何问题转化为空间向量的运算问题 . 应用的核心是充分认识形体特征，进而建立空间直角坐标系，通过向量的运算解答问题，达到几何问题代数化的目的，同时注意运算的准确性 .