- 427.00 KB
- 2021-04-17 发布
2020届高考物理二轮复习非选择题特训练习(5)
功能关系及其与圆周运动的综合应用
1、如图所示,竖直平面内放一直角杆,杆的各部分均光滑,水平部分套有质量为的小球A,竖直部分套有质量为的小球B,A、B之间用不可伸长的轻绳相连。在作用于A球上的水平拉力F的作用下,系统处于静止状态,且,重力加速度.
1.求水平拉力F的大小和水平杆对小球A弹力FN的大小;
2.若改变水平力F大小,使小球A由静止开始,向右做加速度大小为的匀加速直线运动,求经过拉力F所做的功.
2、
如图所示,半径R=0.45m的四分之一光滑圆弧轨道,圆心O与右端点A连线水平,底端距水平地面的高度h=0.2m。一质量m=1.0kg的小滑块(可视为质点)从圆弧轨道顶端A由静止释放。忽略空气阻力,取g=10m/s2。求:
(1)小滑块在圆弧轨道底端B点受到的支持力大小FN;
(2)小滑块落地点与B点的水平距离x。
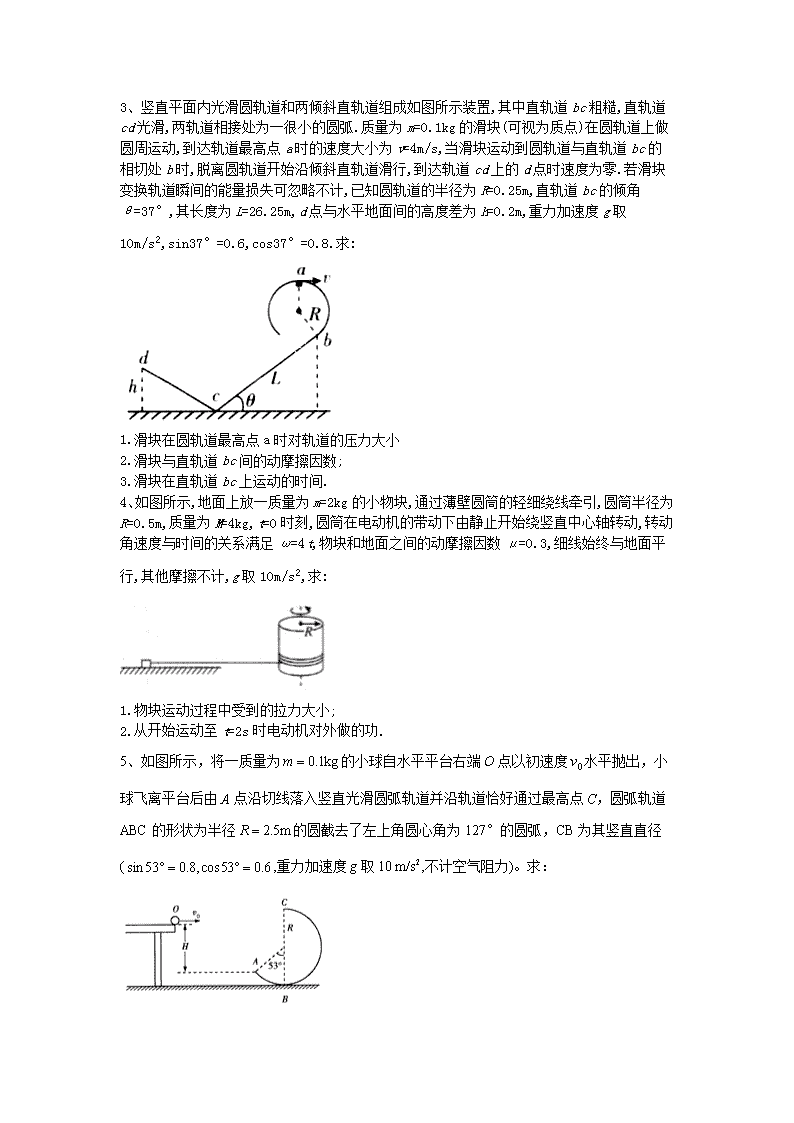
3、竖直平面内光滑圆轨道和两倾斜直轨道组成如图所示装置,其中直轨道bc粗糙,直轨道cd光滑,两轨道相接处为一很小的圆弧.质量为m=0.1kg的滑块(可视为质点)在圆轨道上做圆周运动,到达轨道最高点a时的速度大小为v=4m/s,当滑块运动到圆轨道与直轨道bc的相切处b时,脱离圆轨道开始沿倾斜直轨道滑行,到达轨道cd上的d点时速度为零.若滑块变换轨道瞬间的能量损失可忽略不计,已知圆轨道的半径为R=0.25m,直轨道bc的倾角θ=37°,其长度为L=26.25m,d点与水平地面间的高度差为h=0.2m,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:
1.滑块在圆轨道最高点a时对轨道的压力大小
2.滑块与直轨道bc间的动摩擦因数;
3.滑块在直轨道bc上运动的时间.
4、如图所示,地面上放一质量为m=2kg的小物块,通过薄壁圆筒的轻细绕线牵引,圆筒半径为R=0.5m,质量为M=4kg,t=0时刻,圆筒在电动机的带动下由静止开始绕竖直中心轴转动,转动角速度与时间的关系满足ω=4t,物块和地面之间的动摩擦因数μ=0.3,细线始终与地面平行,其他摩擦不计,g取10m/s2,求:
1.物块运动过程中受到的拉力大小;
2.从开始运动至t=2s时电动机对外做的功.
5、如图所示,将一质量为的小球自水平平台右端O点以初速度水平抛出,小球飞离平台后由A点沿切线落入竖直光滑圆弧轨道并沿轨道恰好通过最高点C,圆弧轨道ABC的形状为半径的圆截去了左上角圆心角为127°的圆弧,CB为其竖直直径(,重力加速度g取10,不计空气阻力)。求:
1.小球经过C点的速度大小;
2.小球运动到轨道最低点B时轨道对小球的支持力大小;
3.平台右端O点到A点的竖直高度H。
6、如图所示,“冰雪游乐场”的滑道由与水平面夹角为60°的光滑直滑道、光滑的1/6圆弧滑道和粗糙的水平滑道构成。一小孩乘坐冰车从滑道的顶端A点由静止滑下,最终停在水平滑道上的D点。已知小孩和冰车的总质量为m,小孩和冰车可视为质点,圆弧滑道的半径为R, 滑道的长度为,滑道连接处均平滑,重力加速度为g,求:
1.小孩乘坐冰车滑至圆弧滑道的最低点C时的速度大小;
2.小孩乘坐冰车滑至圆弧滑道的最低点C时对圆弧滑道的压力大小;
3.小孩乘坐冰车沿水平滑道运动的过程中,克服摩擦力所做的功。
7、如图所示,半径R=1.6m的光滑半圆形轨道固定于竖直平面内,下端与传送带相切于B点,水平传送带上A、B两端点间距L=16m,传送带以v0=10m/s的速度顺时针转动,将质量m=1kg的小滑块(可视为质点)放到传送带上,滑块与传送带间的动摩擦因数μ=0.4,取g=10m/s2
1.将滑块在传送带A端由静止释放,求滑块由释放到第一次经过B端时所需时间;
2.若滑块仍由静止释放,要想滑块能通过圆弧轨道的最高点C,求滑块在传送带上释放的位置范围;
3.若将滑块在传送带中点处释放,同时沿水平方向给滑块一初速度,使滑块能通过圆弧轨道的最高点C, 求此初速度满足的条件.
8、如图甲所示,一竖直平面内的轨道由粗糙斜面AD和光滑圆轨道DCE组成,AD与DCE相切于D点,C为圆轨道的最低点,将一小物块置于轨道ADC上离地面高为H处由静止下滑,用力传感器测出其经过C点时对轨道的压力,改变H的大小,可测出相应的的大小,随H的变化关系如图乙折线PQI所示(PQ与QI两直线相连接于Q点),QI
反向延长交纵轴于F点(0,5.8 N),重力加速度g取,求:
(1)小物块的质量m、圆轨道的半径R及轨道DC所对应的圆心角θ
(2)小物块与斜面AD间的动摩擦因数μ
答案以及解析
1答案及解析:
答案:1.15N;50N; 2.49.5J
解析:1.设静止时绳子与竖直方向夹角为θ,则由已知条件可知
设绳中张力大小为
对B进行受力分析有 解得:
对A进行受力分析有
对A、B整体进行受力分析:竖直方向
2.经过,小球A向右运动的位移此时绳子与水平方向夹角为θ
小球A的速度为
A、B两小球沿绳方向速度大小相等,即
解得
此时小球B上升的高度为
由功能关系知:
2答案及解析:
答案:(1)小滑块从A运动到B过程,机械能守恒,设小滑块运动到B点时,速度大小为v,有
V=3m/s
在B点,根据牛顿第二定律,
解得:
(2)小滑块离开B点后,做平抛运动
水平方向:x=vt
竖直方向:
解得:x=0.6m
解析:
3答案及解析:
答案:1.滑块在圆轨道最高点a时对轨道的压力大小是5.4N
2.0.8; 3.7.66s
解析:1.在圆轨道最高点a处对滑块由牛顿第二定律得
由牛顿第三定律得跨快在圆轨道最高点a时对轨道的压力大小为5.4N
2.对滑块从a点到d点全过程应用动能定理有
解得
3.设滑块在轨道bc上向下滑动的加速度为a1,时间为t1;向上滑动的加速度为a2,时间为t2,在C点时的速度为vc
由c到d有
解得
对从a点到b点的过程,有
解得
在轨道bc上
下滑时:
上滑时:
解得,
由于
由于,滑块在轨道bc上停止后不再下滑.
滑块在直轨道bc上运动的总时间为
4答案及解析:
答案:1.10N; 2.72J
解析:1.由于边缘的线速度与物块的运动速度大小相等, 根据v=ωR=4Rt=2t可知,线速度与时间成正比,物块做初速度为零的匀加速直线运动,加速度为a=2m/s2.
对物块进行受力分析,由牛顿第二定律得T-μmg=ma,则物块受到的拉力大小为T=10N.
2.根据匀变速直线运动规律:t=2s时物块的速度v=at=4m/s,
2s内物块的位移
对整体运用动能定理有
其中
电动机对外做的功为W电=72J
5答案及解析:
答案:1.5m/s 2.6N 3.3.36 m
解析:1.小球恰好通过最高点C时,由重力提供其做圆周运动的向心力,即,则。
2.从B点到C点,由机械能守恒定律得,在B点对小球进行受力分析,由牛顿第二定律得,解得.
3.从A点到B点由机械能守恒定律有,所以,在A点对速度进行分解有,
所以。
6答案及解析:
答案:1. 2. 3.
解析:1.对小孩乘坐冰车从滑道的顶端A点滑至圆弧滑道的M低点C的过程,由机械能守恒定律得,, 解得.
2.可每在C点时圆弧滑道对冰车的支持力为,在C点,由牛顿第二定律得,,又根据牛顿第三定律有,联立解得.
3.对小孩乘坐冰车沿水平滑道运动的过程,由动能定理得,,解得。
7答案及解析:
答案:1.2.85s; 2.滑块在A端与距A端6m的范围内任何一个位置释放均可到达半圆轨道的最高点C处
3.
解析:1.对滑块受力分析,由牛顿第二定律得,,解得
设滑块速度达到时经过的位移为
有
设滑块匀速运动的位移为x2,x2=L-x1=3.5m
则滑块匀速运动的时间为
总时间为t=t1+t2=2.85s.
2.滑块恰好通过C点时有
由机械能守恒定律得
解得滑块通过B点的速度至少为
,解得s=10m,
滑块在A端与距A端6m的范围内任何一个位置释放均可到达半圆轨道的最高点C处;
3.若给滑块一水平向右的初速度,由运动学知识得
解得
所以给滑块一水平向右的速度且需满足的条件为
若给滑块一水平向左的初速度,只需让滑块在向左减速滑行的距离在2〜8m的范围即可,
可得
解得
所以给滑块一水平向左的速度且需满足的条件为
8答案及解析:
答案:(1)由图线知:当时,
此时在最低点有:
解得: m=0.5kg
由图线知:当时,,此时小物块恰好由D点下滑
根据机械能守恒得:
在最低点,根据牛顿第二定律得:
联立解得: R=1m
由几何关系得:
解得:
(2)小球从高为H处的斜面上滑到最低点过程。根据动能定理有:
在最低点,根据牛顿第二定律得:
联立解得:
由图线知,截距为:
解得:
解析: