- 584.50 KB
- 2021-04-17 发布
2012届高考数学考前回归基础训练题——概率统计
一、解答题
1、将A、B两枚骰子各抛掷一次,观察向上的点数,问:
(I)共有多少种不同的结果?
(II)两枚骰子点数之和是3的倍数的结果有多少种?
(III)两枚骰子点数之和是3的倍数的概率为多少?
2、已知10件产品中有3件是次品.
(1)任意取出3件产品作检验,求其中至少有1件是次品的概率;
(2)为了保证使3件次品全部检验出的概率超过0.6,最少应抽取几件产品作检验?
3、甲、乙两个排球队进行比赛,已知每局甲获胜的概率为0.6,比赛是采用五局三胜制。(保留三位有效数字)
(1)在前两局乙队以2 :0领先的条件下,求最后甲、乙队各自获胜的概率。
(2)求甲队获胜的概率。
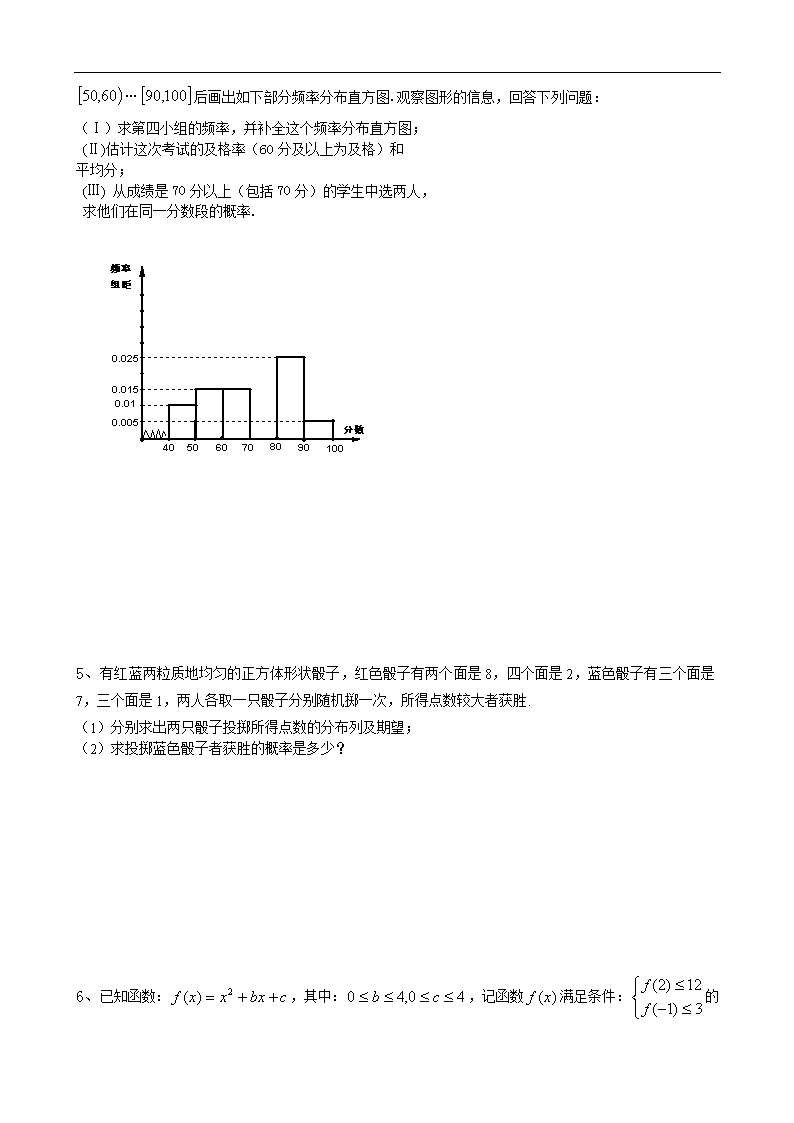
4、某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段,
…后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求第四小组的频率,并补全这个频率分布直方图;
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和
平均分;
(Ⅲ) 从成绩是70分以上(包括70分)的学生中选两人,
求他们在同一分数段的概率.
5、有红蓝两粒质地均匀的正方体形状骰子,红色骰子有两个面是8,四个面是2,蓝色骰子有三个面是7,三个面是1,两人各取一只骰子分别随机掷一次,所得点数较大者获胜.
(1)分别求出两只骰子投掷所得点数的分布列及期望;
(2)求投掷蓝色骰子者获胜的概率是多少?
6、已知函数:,其中:,记函数满足条件:
的事件为A,求事件A发生的概率。
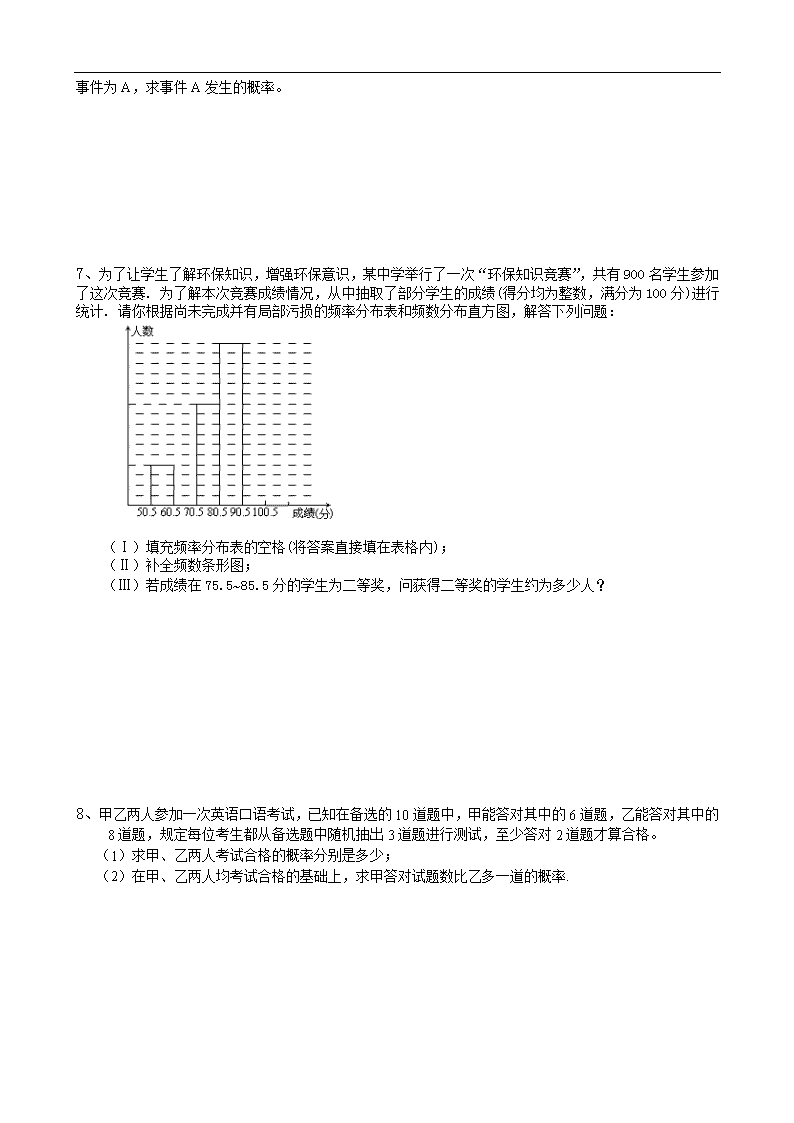
7、为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
8、甲乙两人参加一次英语口语考试,已知在备选的10道题中,甲能答对其中的6道题,乙能答对其中的8道题,规定每位考生都从备选题中随机抽出3道题进行测试,至少答对2道题才算合格。
(1)求甲、乙两人考试合格的概率分别是多少;
(2)在甲、乙两人均考试合格的基础上,求甲答对试题数比乙多一道的概率.
9、某人投掷一枚硬币,出现正面和反面的概率都是,构造数列{an},使
当第n次出现反面时
当第n次出现正面时
,记
(1)求S8=2时的概率;
(2)求S2≠0且S8=2时的概率.
10、一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个. 求:
(Ⅰ)连续取两次都是红球的概率;
(Ⅱ)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,但取球次数最多不超过4次,求取球次数的概率分布列及期望.
11、袋中装着标有数字1,2,3的小球各2个,从袋中任取2个小球,每个小球被取出的可能性都相等.
(Ⅰ)求取出的2个小球上的数字互不相同的概率;
(Ⅱ)用表示取出的2个小球上的数字之和,求随机变量的概率分布与数学期望
12、某商场经销某商品,顾客可采用一次性付款或分期付款购买.根据以往资料统计,顾客采用一次性付款的概率是0.6,经销一件该商品,若顾客采用一次性付款,商场获得利润200元;若顾客采用分期付款,商场获得利润250元.
(Ⅰ)求3位购买该商品的顾客中至少有1位采用一次性付款的概率;
(Ⅱ)求3位顾客每人购买1件该商品,商场获得利润不超过650元的概率.
13、有红蓝两粒质地均匀的正方体形状骰子,红色骰子有两个面是8,四个面是2,蓝色骰子有三个面是7,三个面是1,两人各取一只骰子分别随机掷一次,所得点数较大者获胜.
(1)分别求出两只骰子投掷所得点数的分布列及期望;
(2)求投掷蓝色骰子者获胜的概率是多少?
14、某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2
次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试.假设某学生每次通过测试的概率都是,每次测试时间间隔恰当,每次测试通过与否互相独立.
(1) 求该学生考上大学的概率.
(2) 如果考上大学或参加完5次测试就结束,记该生参加测试的次数为ξ,求ξ的分布列及ξ的数学期望.
15、甲、乙、丙三人分别独立的进行某项技能测试,已知甲能通过测试的概率是,甲、乙、丙三人都能通过测试的概率是,甲、乙、丙三人都不能通过测试的概率是,且乙通过测试的概率比丙大.
(Ⅰ)求乙、丙两人各自通过测试的概率分别是多少;
(Ⅱ)求测试结束后通过的人数的数学期望.
16、已知射手甲射击一次,击中目标的概率是.
(1)求甲射击5次,恰有3次击中目标的概率;
(2)假设甲连续2次未击中目标,则中止其射击,求甲恰好射击5次后,被中止射击的概率
17、已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.
(1)求甲射击一次,命中不足8环的概率;
(2)求甲射击一次,至少命中7环的概率.
18、 旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条.
(1)求3个旅游团选择3条不同的线路的概率
(2)求恰有2条线路没有被选择的概率.
(3)求选择甲线路旅游团数的期望.
19、将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入袋或袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是.
(1求小球落入袋中的概率;
(2)容器入口处依次放入4个小球,记为落入袋中的小球个数,试求的概率和的数学期望.
20、已知集合,在平面直角坐标系中,点的坐标x∈A,y∈A。计算:
(1)点正好在第二象限的概率;
(2)点不在x轴上的概率;
(3)点正好落在区域上的概率。
以下是答案
一、解答题
1、解: (I) 共有种结果
(II) 若用(a,b)来表示两枚骰子向上的点数,则点数之和是3的倍数的结果有:
(1,2),(2,1),(1,5),(5,1),(2,4),(4,2),
(3,3),(4,5),(5,4),(3,6),(6,3),(6,6)
共12种.
(III)两枚骰子点数之和是3的倍数的概率是:P=
2、(1)解:任意取出3件产品作检验,全部是正品的概率为
至少有一件是次品的概率为
(2)设抽取n件产品作检验,则3件次品全部检验出的概率为
由得:
整理得:,
∵n∈N*,n≤10,∴当n = 9或n = 10时上式成立
∴任意取出3件产品作检验,其中至少有1件是次品的概率为;为了保证使3件次品全部检验出的概率超过0.6,最少应抽取9件产品作检验
3、(1)设最后甲获胜为事件A,乙获胜为事件B
(2)设甲获胜为事件C,其比分可能为3:0,3:1,3:2
4、(Ⅰ)因为各组的频率和等于1,故第四组的频率:
直方图如右所示
(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,
频率和为
所以,抽样学生成绩的合格率是%.
利用组中值估算抽样学生的平均分
=
=71
估计这次考试的平均分是71分
(Ⅲ), ,”的人数是18,15,3。所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。
5、解:(1)设红色骰子投掷所得点数为,其分布如下:
8
2
P
;
设蓝色骰子投掷所得点数,其分布如下;
7
1
P
(2)∵投掷骰子点数较大者获胜,∴投掷蓝色骰子者若获胜,则投掷后蓝色骰子点数为7,
红色骰子点数为2.∴投掷蓝色骰子者获胜概率是
6、解:由,可得:
知满足事件A的区域:的面积10,而满足所有条件的区域的面积:
从而,得:,
答:满足事件A的概率为
7、解:(1)
分组
频数
频率
50.5~60.5
4
0.08
60.5~70.5
8
0.16
70.5~80.5
10
0.20
80.5~90.5
16
0.32
90.5~100.5
12
0.24
合计
50
1.00
(2) 频数直方图如右上所示
(3) 成绩在75.5~80.5分的学生占70.5~80.5分的学生的,因为成绩在70.5~80.5分的学生频率为0.2 ,所以成绩在76.5~80.5分的学生频率为0.1 ,
成绩在80.5~85.5分的学生占80.5~90.5分的学生的,因为成绩在80.5~90.5分的学生频率为0.32 ,所以成绩在80.5~85.5分的学生频率为0.16
所以成绩在76.5~85.5分的学生频率为0.26,
由于有900名学生参加了这次竞赛,
所以该校获得二等奖的学生约为0.26´900=234(人)
8、(1)设A={甲考试合格},B={乙考试合格},
(2)甲答对三道,乙答对两道题的概率为
9、解:(1)S8=2时,需8次中有5次正面3次反面,设其概率为P1,
则P1=
(2)S2≠0即前两次同时出现正面或反面,
当同时出现正面时,S2=2,要S8=2需6次3次正面3次反面,设其概率为P2,
则P2=
当同时出现反面时,S2=-2,要S8=2需后6次5次正面1次反面,设其概率为P3,
则P3=
所以S2≠0且S8=2时的概率为
10、解:(Ⅰ)连续取两次都是红球的概率
(Ⅱ)的可能取值为1,2,3,4,,,
,.
的概率分布列为
E=1×+2×+3×+4×=.
1
2
3
4
P
11、(Ⅰ)解法一:记“取出的2个小球上的数字互不相同”为事件,
∵从袋中的6个小球中任取2个小球的方法共有种,
其中取出的2个小球上的数字互不相同的方法有,
∴.
解法二:记“取出的2个小球上的数字互不相同”的事件记为,“取出的2个小球上的数字相同”的事件记为,则事件与事件是对立事件.
∵,
∴.
(Ⅱ)解:由题意,所有可能的取值为:2,3,4,5,6.
,,,
,.
故随机变量的概率分布为
2
3
4
5
6
因此,的数学期望.
12、解:(Ⅰ)记表示事件:“位顾客中至少位采用一次性付款”,则表示事件:“位顾客中无人采用一次性付款”.
,
.
(Ⅱ)记表示事件:“位顾客每人购买件该商品,商场获得利润不超过元”.
表示事件:“购买该商品的位顾客中无人采用分期付款”.
表示事件:“购买该商品的位顾客中恰有位采用分期付款”.
则.
,.
.
13、解:(1)设红色骰子投掷所得点数为,其分布如下:
8
2
P
;
设蓝色骰子投掷所得点数,其分布如下;
7
1
P
(2)∵投掷骰子点数较大者获胜,∴投掷蓝色骰子者若获胜,则投掷后蓝色骰子点数为7,
红色骰子点数为2.∴投掷蓝色骰子者获胜概率是
14、(1)记“该生考上大学”的事件为事件A,其对立事件为,则P()=C
∴P(A)=1----4’ 答:该生考上大学的概率为
(2)参加测试次数ξ的可能取值为2,3,4,5,
P(ξ=2)=, P(ξ=3)=C ,
P(ξ=4)=C, P(ξ=5)=C
ξ
2
3
4
5
P
故ξ的分布列为:
Eξ=2×+3×+4×+5×=
15、解(Ⅰ)设乙、丙两人各自通过测试的概率分别是、依题意得:
即 或 (舍去)
所以乙、丙两人各自通过测试的概率分别是、.
(Ⅱ)因为
所以=
16、解:(1)设“甲射击5次,恰有3次击中目标”为事件A,则
.
答:甲射击5次,恰有3次击中目标的概率为.
(2)方法1:设“甲恰好射击5次后,被中止射击”为事件C,由于甲恰好射击5次后被中止射击,所以必然是最后两次未击中目标,第三次击中目标,第一次与第二次至少有一次击中目标,则
.
答:甲恰好射击5次后,被中止射击的概率为.
方法2:设“甲恰好射击5次后,被中止射击”为事件C,由于甲恰好射击5次后被中止射击,所以必然是最后两次未击中目标,第三次击中目标,第一次与第二次至少有一次击中目标,则
.
答:甲恰好射击5次后,被中止射击的概率为.
17、解:记“甲射击一次,命中7环以下”为事件,“甲射击一次,命中7环”为事件,由于在一次射击中,与不可能同时发生,故与是互斥事件,
(1)“甲射击一次,命中不足8环”的事件为,
由互斥事件的概率加法公式,.
答:甲射击一次,命中不足8环的概率是0.22.
(2)方法1:记“甲射击一次,命中8环”为事件,“甲射击一次,命中9环(含9环)以上”为事件,则“甲射击一次,至少命中7环”的事件为,
∴.
答:甲射击一次,至少命中7环的概率为0.9.
方法2:∵“甲射击一次,至少命中7环”为事件,
∴=1-0.1=0.9.
答:甲射击一次,至少命中7环的概率为0.9.
18、解:(1)3个旅游团选择3条不同线路的概率为:P1=
(2)恰有两条线路没有被选择的概率为:P2=
(3)设选择甲线路旅游团数为ξ,则ξ=0,1,2,3
P(ξ=0)= P(ξ=1)=
P(ξ=2)= P(ξ=3)=
∴ξ的分布列为:
ξ
0
1
2
3
P
∴期望Eξ=0×+1×+2×+3×=
19、解:(1记“小球落入袋中”为事件,“小球落入袋中”为事件,则事件的对立事件为,而小球落入袋中当且仅当小球一直向左落下或一直向右落下,故
,
从而;
(2)显然,随机变量,故
,
.
20、解:满足条件的点共有个
(1)正好在第二象限的点有
,,,,,
故点正好在第二象限的概率.
(2)在x轴上的点有,,,,,
故点不在x轴上的概率.
(3)在所给区域内的点有,,,,,
故点在所给区域上的概率
答:(1)点正好在第二象限的概率是,(2)点不在x轴上的概率是,(3)点在所给区域上的概率